Almagesto: Sistema Ptolemaico o Sistema Geocéntrico
| Ir a la Bibliografía | Contenidos |
Definiciones
La Tierra es el centro del Universo (Geocentrismo: Geo = Tierra, centrismo = centrado en la) y esta no tiene ningún movimiento de un lugar a otro [1]. Ver en el Almagesto: Libro I Capítulos: 5, 6, 7 y 8.
El orden de las luminarias entorno a la Tierra es: Luna, Mercurio, Venus, Sol, Marte, Júpiter, Saturno y las Estrellas. En la siguiente figura se representa solamente la Tierra y el Sol.

La teoría solar, lunar y planetaria de Ptolomeo tienen los mismos principios: se mueven sobre epiciclos (del griego, epi, sobre, y kyklos, círculo, es decir "sobre el círculo") y estos a su vez sobre deferentes (círculo descrito por el centro del epiciclo). Se sabe que este sistema de deferentes y epiciclos fue diseñado por Apolonio de Perge (S. III a. C.).
Deferente y Epiciclo
Para los PLANETAS INTERIORES (Mercurio y Venus), en la Figura 2 la órbita del planeta se describe como un círculo con el Sol S en su centro y este último en un círculo alrededor de la Tierra T.

Por lo tanto la descripción geocéntrica del movimiento de un planeta interior esta dada por un planeta que se mueve sobre un pequeño círculo cuyo centro es transportado sobre un círculo mayor cuyo centro es la Tierra. El pequeño círculo lo llamamos “epiciclo”, el mayor “deferente”. Desde la Tierra T el planeta P parece moverse sobre un círculo cuyo centro S se mueve alrededor de T. Por lo tanto tenemos nuevamente un movimiento epicíclico. Ver Heráclides Póntico.
En el caso de los PLANETAS EXTERIORES (Marte, Júpiter y Saturno) con el fin de establecer una similitud con el caso de los planetas interiores introducimos un punto C tal que los cuatro puntos S, T, P y C siempre forman un paralelogramo. SP es el radio de la órbita planetaria; dado que TC = SP vemos que C se ubica sobre un círculo con centro en T. Similarmente TS es el radio de la órbita solar, y dado que TS = CP, vemos que P se ubica sobre un círculo alrededor de C.
Por lo tanto el planeta P se mueve sobre un epiciclo cuyo centro C recorre una deferente cuyo centro es T. En consecuencia hemos establecido una analogía exacta para el caso de los planetas interiores. En ambos casos el planeta tiene un movimiento epicíclico. En el caso de los planetas interiores el centro del epiciclo C coincide con el Sol S. Para los planetas exteriores el centro del epiciclo C se mueve alrededor de T con la misma velocidad angular como el planeta se mueve alrededor del Sol, mientras el planeta P se mueve sobre un epiciclo alrededor de C con la misma velocidad angular tal como se mueve el Sol S alrededor de la Tierra T. Ver en el Almagesto: Hipótesis de la Excéntrica y del Epiciclo.
Excéntrica
Hemos visto que las órbitas planetarias con respecto a la Tierra (como centro) consisten en epiciclos cuyos centros se mueven con una velocidad uniforme sobre deferentes teniendo como centro la Tierra. En otras palabras, si omitimos las pequeñas excentricidades de las órbitas planetarias y si también obviamos las pequeñas inclinaciones de estas órbitas, luego el movimiento epicíclico da una descripción correcta de las órbitas planetarias con respecto a la Tierra. La excentricidad de las órbitas (excéntricas, es decir fuera del centro) pueden ser tomadas en consideración asumiendo imperceptiblemente las posiciones excéntricas de la Tierra con respecto a los centros de las deferentes. Las latitudes pueden ser tomadas en cuenta para darles a los epiciclos sus propias inclinaciones. Ambos procedimientos fueron estudiados por los astrónomos griegos.
Nuevamente, entonces, hemos visto que los planetas se mueven con respecto a la Tierra sobre epiciclos. Esto hace particularmente sencillo entender las formas de los movimientos planetarios vistos desde la Tierra.
Comencemos nuevamente con los PLANETAS INTERIORES. Sus velocidades angulares alrededor del centro S de su epiciclo (Figura 2) es mayor que la velocidad angular de S alrededor de la Tierra T. Si el planeta P esta sobre una parte de su epiciclo el cuál se desplaza visto desde la Tierra, el movimiento de P es sumado al movimiento de S y el movimiento planetario parece mayor que el movimiento de S. Llamamos esto movimiento “directo”.
Sin embargo, entre A y B, el planeta se mueve hacia atrás más rápido que su epiciclo siendo transportado hacia adelante. Es fácil ver que los puntos A y B se ubican algo dentro de los dos puntos donde las líneas desde T son tangenciales al epiciclo, por lo tanto este parece tener un movimiento “retrógrado”.
Ahora en los PLANETAS EXTERIORES, el movimiento del planeta es más despacio con respecto al del Sol. El movimiento retrógrado ocurre cerca de la oposición, cuando el Sol y el planeta son vistos en direcciones opuestas desde la Tierra. Consecuentemente el movimiento retrógrado de un planeta exterior es completamente visible en contraste con aquel de un planeta interior, donde una parte del movimiento retrógrado comienza a ser invisible cerca de la conjunción inferior. Un planeta exterior comienza a ser invisible solo una vez en cada ciclo (conjunción con el Sol).
Entonces, según lo visto, las órbitas planetarias circulares con el Sol como centro son movimientos epicíclicos con respecto a un observador terrestre. Es fácil de ver, por el mismo método, que las órbitas circulares excéntricas conducen a movimientos epicíclicos con deferentes excéntricas, la excentricidad siendo la resultante de los vectores que representan la excentricidad planetaria y solar (o terrestre).
Ecuante
Este modelo más tarde fue modificado por Ptolomeo sobre la base de sus observaciones mayormente realizadas por él mismo y por su predecesor Teón de Esmirna (contemporáneo); Ptolomeo encontró que el centro del epiciclo parecía moverse con su velocidad angular media no con respecto al centro de la deferente sino con respecto a un punto (más tarde llamado “ecuante”) localizado simétricamente al observador, por lo tanto también un movimiento aparente del Planeta visto desde la Tierra (observador). Entonces, en la Figura 3, este nuevo punto "ecuante" E se encuentra a la misma distancia e que tiene el observador O al centro de la deferente G pero en sentido opuesto (EG = GO). Ver en el Almagesto: Hipótesis de los Planetas.
Hemos encontrado esencialmente la misma idea en la teoría lunar de Ptolomeo donde el centro C del epiciclo se esta moviendo con una velocidad angular constante solo en la medida que este se ubique sobre el radio OT que se mueve uniformemente mientras la velocidad lineal de C no es constante.
Mentes filosóficas consideran a esto último una “salida” del estricto movimiento circular uniforme como la objeción más seria en contra al sistema ptolemaico y de combinaciones inventadas extremadamente complicadas de movimientos circulares con el fin de rescatar el axioma primitivo de la simpleza de un Universo esférico.
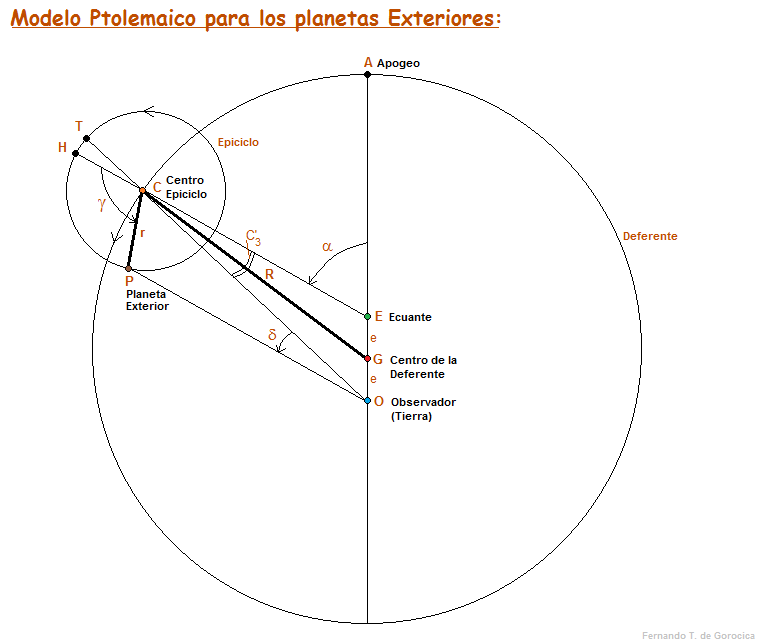
La figura de arriba representa el modelo de Ptolomeo para los PLANETAS EXTERIORES (Marte, Júpiter y Saturno). El movimiento medio del planeta esta representado por el movimiento del centro C del epiciclo, medido por α (alfa) la “longitud media” de C desde el apogeo A de la deferente. El planeta P se mueve sobre un epiciclo con una velocidad correspondiente al período sinódico y medido por γ (gama), la “anomalía”. Ver en el Almagesto: Sobre las Vueltas Periódicas de los cinco Planetas.
El sentido de rotación de P sobre el epiciclo es ahora igual al sentido del movimiento medio, por lo tanto dándole al planeta su mayor movimiento directo cerca del apogeo del epiciclo y generando un movimiento retrógrado cerca del perigeo.
De acuerdo con nuestro análisis general del movimiento geocéntrico (Figura 2) la dirección CP es paralela a la dirección desde O (T) hasta la longitud media del Sol S, en el caso de un planeta exterior.
En el caso de un planeta interior el ángulo α se incrementa tanto como la longitud media del Sol (de hecho C puede ser identificado como la longitud media del Sol S) y la anomalía γ varía independientemente de la posición del Sol.
En todos los casos la posición P depende de dos variables independientes α y γ que pueden ser consideradas conocidas en algún instante t.

La figura anterior es para Mercurio (PLANETA INTERIOR), donde sus observaciones pueden no estar relacionadas con un modelo simple como lo es para los otros planetas: dice Urbain Le Verrier “Nulle planète n’a demandé aux astronomers plus de soins et de peines que Mercure, et ne leur a donné en récompense tant d’inquiétudes, tant de contrariétes”.
Los datos de Ptolomeo nos lleva nuevamente a la necesidad de incrementar el tamaño aparente del epiciclo como sucede en el caso de la Luna, la única diferencia es que la máxima aproximación (perigeo planetario) ahora ocurre alrededor de ± 120° desde la línea de los ápsides (ABEO). Por lo tanto Ptolomeo adopta un modelo como el descrito en la Figura 4. El centro G de la deferente se mueve de manera retrógrada sobre un círculo de radio e y con centro en B donde e no solo es la excentricidad BE sino también es la distancia del observador O desde la ecuante E (BE = EO).
El centro C del epiciclo se mueve hacia adelante tal que su progreso, visto desde E, parece uniforme y por la misma cantidad de G se reubica en la dirección opuesta desde la línea apsidal AO. Para α = ± 120° el radio GC de la deferente pasa a través de E y por lo tanto lleva a C más cerca de O que cuando α = 180°.
En otras palabras la órbita de C con respecto a O tiene un apogeo en la línea apsidal pero dos perigeos simétricos a él cuando α = ± 120°.
Tablas de los Movimientos y de las Proporciones Orbitales
| Astro | Vueltas del Astro sobre el Epiciclo [Año] | Movimiento Medio en Anomalía del Astro [Días/Sinódico] | Movimiento Medio en Longitud del Centro del Epiciclo (α) [°/Sinódico] | Movimiento Medio en Anomalía del Astro (γ) [°/Año] | Movimiento Medio en Longitud del Centro del Epiciclo (α) [°/Año] |
|---|---|---|---|---|---|
| Luna | 12,19075 | 29,530589 | 389° 06' 22,79" | 4771° 56' 29,18" | 4452° 37' 46,86" |
| Mercurio | 3,10670 | 115,878621 | 114° 12' 50,60" | 1134° 42' 41,29" | 360° (Sol) |
| Venus | 0,61651 | 583,933333 | 575° 32' 43,06" | 225° 10' 39,94" | 360° (Sol) |
| Sol (Hipótesis del Epiciclo) | 1 | --- | --- | 360° | 360° |
| Marte | 0,46157 | 779,938288 | 408° 44' 03,24" | 168° 35' 20,17" | 191° 24' 39,83" |
| Júpiter | 0,90251 | 398,886410 | 33° 09' 23,08" | 329° 38' 23,31" | 30° 21' 36,69" |
| Saturno | 0,95215 | 378,092982 | 16° 07' 26,60" | 347° 46' 06,32" | 15° 34' 34,38" |
El Año Solar según Ptolomeo es de 365,246666666666 días, cantidad que he utilizado para los valores sexagesimales. Ptolomeo utilizó el año de 365 días del calendario Egipcio para calcular las expresiones en el sistema sexagesimal.
La longitud media (α) es el movimiento medio del centro del epiciclo sobre la deferente.
El movimiento en anomalía (γ) es el movimiento medio del planeta sobre el epiciclo.
La animación siguiente, Figura 5, representa el movimiento epicíclico de Júpiter entre tres oposiciones diferentes, es decir cuando el planeta se encuentra en línea recta con la Tierra y el Sol (Elongación ~180°).

Observar que la oposición de Júpiter ocurre casi en medio del recorrido del movimiento retrógrado planetario, en el “bucle” que describe en el cielo nocturno y la conjunción con el Sol, “detrás” del mismo, en medio del recorrido del movimiento directo.
La diferencia angular entre los centros del epiciclo entre dos oposiciones esta dada en la tabla anterior, siendo de 33° 09' 23,08" [°/Sinódico].
La deferente y el epiciclo joviano están en proporción con las partes descritas en la tabla siguiente. Los movimientos uniformes circulares, la excéntrica del Sol y el epiciclo de Júpiter también están de acuerdo a lo descrito en la Figura 2.
| Astro | Radio Deferente (AG) | Centro Deferente (G) a la Excéntrica (O) / Ecuante (E) = (e) | Radio Epiciclo (r = CP) | Movimiento Retrógrado [°] |
|---|---|---|---|---|
| Luna | 49;41p | 10;19p | 5;15p | --- |
| Mercurio | 60p | 3p | 22;30p | 15;12,46 |
| Venus | 60p | 1 ¼p | 43;10p | 14;4,38 |
| Sol (Hipótesis del Epiciclo) | 60p | E y O coinciden con G | 2;30p | --- |
| Marte | 60p | 6p | 39;30p | 11;12,14 |
| Júpiter | 60p | 2;45p | 11;30p | 9;54,40 |
| Saturno | 60p | 3;25p | 6;30p | 7;18,10 |
Los valores de las partes (p) de esta última tabla, en la notación moderna, por ej. en Saturno: 3;25p (en sistema sexagesimal), debe leerse en el sistema decimal 3 + 25 / 60, es decir 3,41666666666p. En el caso del movimiento retrógrado, por ej. en Saturno: 7;18,10, debe leerse en el sistema sexagesimal 7° 18' 10" y en el sistema decimal: 7 + 18 / 60 + 10 / 3600, es decir 7,302777777777.
| Ir a la Bibliografía | Contenidos |
Notas de referencia
- ↑ Traductor al español: Resumen del Sistema Geocéntrico o Ptolemaico. Fuente: “The Exact Sciences in Antiquity”, Capítulo V: "Babylonian Astronomy" y Apéndice I: "The Ptolemaic System". Autor: Otto E. Neugebauer. Editorial: Dover Publications, Inc. Segunda Edición. New York. 1957.
- ↑ Tablas, datos y animación según el Almagesto de Claudio Ptolomeo y confeccionadas por el traductor al español.