Almagesto: Libro IX - Capítulo 10
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre la corrección de los Movimientos Periódicos de Mercurio}
La secuela de lo anterior es el establecimiento de los movimientos periódicos de Mercurio y de sus épocas [2]. Ahora el [movimiento y la época] en longitud, es decir, del Epiciclo en su movimiento uniforme alrededor del punto G, están dados inmediatamente desde aquellos del Sol. En cuanto al [movimiento y época] en anomalía, esto es, del planeta en su movimiento [uniforme] sobre el epiciclo alrededor del centro del epiciclo, lo hemos derivado de dos observaciones confiables, una de entre las registradas en nuestro tiempo, y la otra desde las observaciones [más] antiguas.
[Primero], observamos el planeta Mercurio por medio del instrumento Astrolabio en el segundo año de Antonino Pío (que fue en el 886 to. año de Nabonassar, 2/3 de Epiphi [XI] en el calendario Egipcio [17/18 de Mayo de 139]. Este aún no había alcanzado su Máxima Elongación como estrella de la tarde. Cuando fue avistado con respecto a la estrella en el corazón de Leo fue observado en una longitud de ♊︎ 17 ½º; y en aquel momento este también estuvo a 1 ⅙º hacia atrás desde el centro de la Luna. La hora en Alejandría fue 4 ½ horas equinocciales antes de la medianoche del 3 [2/3 de Epiphi] [3], dado que, de acuerdo al astrolabio, los 12 mos. grados de Virgo [ej. ♍︎ 11º - 12º] estuvieron culminando, mientras el Sol estuvo alrededor de ♉︎ 23º. Ahora, en aquel momento, las posiciones de acuerdo a las hipótesis que hemos demostrado fueron las siguientes [4]:
| Longitud media del Sol | ♉︎ 22;34º |
| Longitud media de la Luna | ♊︎ 12;14º |
| Anomalía de la Luna desde el apogeo del epiciclo | 281;20º |
| En consecuencia, por cálculo, la posición verdadera del centro de la Luna | ♊︎ 17;10º |
| Posición aparente del centro de la Luna | ♊︎ 16;20º |
Por lo tanto desde este [cálculo] también encontramos que la longitud de Mercurio fue de ♊︎ 17 ½º (dado que este estuvo a 1 ⅙º hacia atrás desde el centro de la Luna).
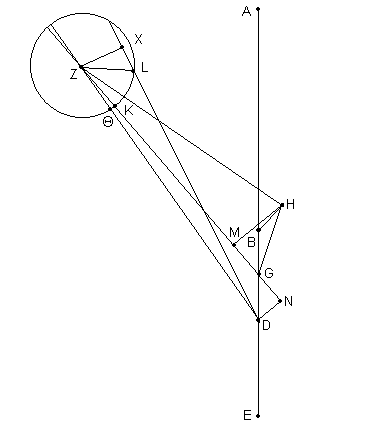
Con esto como dato, sea ABGDE [Fig. 9.9] el diámetro a través del apogeo y del perigeo [5], sobre el cuál el punto A es tomado como el apogeo, B como el punto alrededor del cual el centro de la Excéntrica realiza su movimiento hacia adelante, y G el punto alrededor del cual el centro del epiciclo realiza su movimiento [uniforme] hacia atrás, y D el centro de la Eclíptica. Sea Z el centro del epiciclo, habiendo sido transportado por la línea GZ alrededor del punto G a través del ángulo AGZ, y sea H el centro de la excéntrica, habiendo sido transportado por la línea BH alrededor del punto B a través del ángulo ABH, que será, obviamente, igual al ^ AGZ por la misma velocidad de los movimientos. Dibujar ΘKL, el epiciclo con centro en Z, y sea ubicado el planeta en L. Unir GH, HZ, DZ, ZL y DL, prolongar GZΘ y eliminar las perpendiculares HM y DN hasta él desde H y D, y eliminar la perpendicular ZX desde Z hasta DL.
Consideremos el problema, de encontrar el arco del epiciclo entre Θ, el apogeo [del epiciclo], y el planeta en L.
Ahora, en aquel instante, la longitud media del Sol fue de ♉︎ 22;34º, y el perigeo del planeta estuvo alrededor de ♈︎ 10º [6].
Por lo tanto su distancia desde el perigeo en longitud media fue de 42;34º.
En consecuencia ^ GBH = 42;34º donde los 4 ángulos rectos = 360º
En consecuencia ^ GBH = 85;8ºº donde los 2 ángulos rectos = 360ºº.
Y dado que BG es siempre igual a BH
^ BHG = ^ BGH = 137;26ºº en las mismas unidades.
Entonces, en el círculo alrededor del triángulo BGH [7]
arco HG = 85;8º
y arco BG = 137;26º.
Por lo tanto las cuerdas correspondientes
GH = 81;10p donde el diámetro del círculo es de 120p.
y BG = 111;49p donde el diámetro del circulo es de 120p.
Por lo tanto donde BG = 3p, GH = 2;11p.
Nuevamente, dado que ^ BGH = 137;26ºº donde 2 ángulos rectos = 360ºº,
y ^ BGM = 85;8ºº donde 2 ángulos rectos = 360ºº,
por sustracción, ^ HGM = 52;18ºº en las mismas unidades.
Por lo tanto en el círculo alrededor del triángulo rectángulo GHM
arco HM = 52;18º
y arco GM = 127;42º (suplementario).
Por lo tanto las cuerdas correspondientes
HM = 52;53p donde la hipotenusa GH = 120p
y GM = 107;43p donde la hipotenusa GH = 120p.
Por lo tanto donde GH = 2;11p,
y HZ, el radio de la excéntrica transportando el epiciclo, es de 60p,
HM = 0;58p
y GM = 1;58p.
Por ende MZ, siendo una cantidad insignificantemente menor que HZ, la hipotenusa [del triángulo HMZ], es la misma, 60p,
y por sustracción [de GM desde MZ], GZ = 58;2p.
Similarmente, dado que ^ DGN = 85;8ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo GDN
arco DN = 85;8º
y arco GN = 94;52º (suplementario).
Por lo tanto las cuerdas correspondientes
DN = 81;10p donde la hipotenusa GD = 120p
y DN = 88;23p donde la hipotenusa GD = 120p.
Por lo tanto donde GD = 3p y, como fue demostrado, GZ = 58;2p,
DN = 2;2p
y GN = 2;13p;
Y, por sustracción [de GN desde GZ], NZ = 55;49p.
Por lo tanto la hipotenusa DZ [= (DN² + NZ²) ^ 0,5] ≈ 55;51p donde el radio del epiciclo = 22;30p.
Por lo tanto en el círculo alrededor del triángulo rectángulo DZN,
donde la hipotenusa DZ = 120p,
DN = 4;22p
y arco DN = 4;11º.
En consecuencia ^ DZN = 4;11ºº donde 2 ángulos rectos = 360ºº,
y, por adición [de ^ DZN y ^ DGN], ^ EDZ = 89;19ºº.
Y el ángulo total EDL = 135ºº en las mismas unidades, dado que el planeta fue
observado en los 67;30º desde el perigeo.
Por lo tanto por sustracción [del ^ EDZ desde el ^ EDL], ^ ZDL = 45;41ºº. Por lo tanto en el círculo alrededor del triángulo rectángulo DZX,
arco ZX = 45;41º
y ZX = 46;35p donde la hipotenusa DZ = 120p.
Por lo tanto donde La hipotenusa DZ = 55;51p y el radio del epiciclo,
ZL = 22;30p,
ZX = 21;41p.
Y, en el círculo alrededor del triángulo rectángulo ZLX,
donde la hipotenusa ZL = 120p,
ZX = 115;39p.
En consecuencia arco ZX = 149;2º [8]
y ^ ZLX = 149;2ºº donde 2 ángulos rectos = 360ºº.
Pero demostramos que el ^ ZDL = 45;41ºº en las mismas unidades.
[En consecuencia ^ LZK = ^ ZLX + ^ ZDL = 194;43ºº.]
E igualmente ^ ΘZK [= ^ DZN] = 4;11ºº.
Por lo tanto, por adición [de ^ ΘZK + ^ LZK],
^ ΘZL = 198;54ºº donde 2 ángulos rectos = 360ºº
^ ΘZL = 99;27º donde 4 ángulos rectos = 360º.
Por lo tanto el arco ΘKL del epiciclo, que fue en aquella observación la distancia del planeta Mercurio desde el apogeo Θ, es de 99;27º.
Lo que se ha requerido para examinar.
[Segundo], en el 21 er. año del calendario de Dionysius (que fue en el 484 to. año desde [la era de] Nabonassar), 22 de Scorpion, [que es el] 18/19 de Thoth [I] en el calendario Egipcio [14/15 de Noviembre de -264], en el amanecer, Stilbon [por ej. Mercurio] estuvo a 1 Luna hacia atrás de la línea recta [que va] a través de la [estrella] Norte (septentrional) en la frente de Scorpius y la [estrella] del medio [en la frente], y estuvo 2 Lunas hacia el Norte de la [estrella] Norte en la frente. Ahora, de acuerdo con nuestras coordenadas en aquel instante la de más del medio de esas estrellas en la frente de Scorpius tuvo una longitud de ♏︎ 1 ⅔º, y la misma cantidad [de 1 ⅔º] de la Eclíptica, mientras que la estrella de más al Norte tuvo una longitud de ♏︎ 2 ⅓º y esta a 1 ⅓º al Norte de la Eclíptica [9]. Entonces el planeta Mercurio tuvo una longitud de alrededor de ♏︎ 3 ⅓º [10]. Además esta claro que [Mercurio] no había alcanzado aún su máxima elongación como estrella de la mañana, ya que 4 días más tarde, en el 26 de Scorpion, se registra que su distancia desde la misma línea recta hacia atrás fue de 1 ½ Lunas; [en ese instante] su elongación llegó a la máxima, el Sol se ha movido por alrededor de 4 grados, pero el planeta a [sólo] mitad de una Luna. Y en el amanecer del 19 de Thoth la longitud media del Sol, de acuerdo con nuestras tablas, fue de ♏︎ 20 ⅚, mientras la longitud del apogeo del planeta fue de ♎︎ 6º, dado que los más o menos 400 años entre las observaciones producen un desplazamiento del apogeo por alrededor de 4º.
Con los datos de arriba, entonces, dibujemos una figura [Fig. 9.10] similar a la precedente [Fig. 9.9], pero en la cual, debido a la diferencia en sus posiciones, los ángulos hacia el apogeo A [por ej. el ^ AGZ y el ^ ABH] han de estar dibujados como agudos, las líneas rectas uniendo [los puntos] hasta el planeta [por ej. la ZL y la DL], hacia delante del [centro] del epiciclo, y la perpendicular ZX más allá de ZL, el radio del epiciclo [11].
Entonces, dado que la posición media del planeta fue de (♏︎ 20 ⅚ - ♎︎ 6º =) 44;50º desde el apogeo.
^ ABH = 44;50º donde 4 ángulos rectos = 360º
^ ABH = 89;40ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto su suplementario, el ^ GBH = 270;20ºº
y el ^ BGH = ^ BHG = 44;50ºº en las mismas unidades.
Y, por el mismo razonamiento [como antes]
en el círculo alrededor del triángulo BGH las cuerdas correspondientes
GH = 84;36p donde el diámetro es de 120p
y BG = BH = 45;46p donde el diámetro es de 120p.
Por lo tanto donde BG = BH = 3p,
GH = 5;33p.
Nuevamente, por hipótesis,
el ^ AGZ = 89;40ºº donde 2 ángulos rectos = 360ºº
y el ^ BGH = 44;50ºº en las mismas unidades,
entonces, por adición, el ^ ZGH = 134;30ºº,
Y, en el círculo alrededor del triángulo rectángulo GHM
arco HM = 134;30º
y arco GM = 45;30º (suplementario).
Por lo tanto las cuerdas correspondientes
MH = 110;40p donde la hipotenusa GH = 120p
y GM = 46;24p donde la hipotenusa GH = 120p.
Por lo tanto donde GH = 5;33p (por ej. donde ZH, el radio de la Excéntrica, es de 60p),
HM = 5;7p
y GM = 2;10p [12].
En consecuencia calculamos ZM [= (ZH² - HM²) ^ 0,5] como 59;47p,
y, por adición [de MG a ZM], ZMG como 61;57p en las mismas unidades.
Similarmente, dado que ^ DGN [= ^ AGZ] = 89;40ºº donde 2 ángulos rectos = 360ºº, en el círculo alrededor del triángulo rectángulo GDN,
arco DN = 89;40º
y arco GN = 90;20º (suplementario).
Entonces las cuerdas correspondientes
DN = 84;36p donde la hipotenusa GD = 120p
y GN = 85;6p donde la hipotenusa GD = 120p.
Por lo tanto donde GD = 3p,
DN = 2;7p
y GN = 2;8p,
y, por adición [de ZG a GN], ZGN = 64;5p.
Por lo tanto la hipotenusa ZD [= (ZN² + DN²) ^ 0,5] = 64;7p en las mismas unidades. Por lo tanto, en el círculo alrededor del triángulo rectángulo ZDN,
donde ZD = 120p,
DN = 3;58p
y arco DN = 3;48º [13].
En consecuencia ^ DZN = 3;48ºº donde 2 ángulos rectos = 360ºº,
y, por sustracción [del ^ DZN desde el ^ AGZ],
^ ADZ = 85;52ºº en las mismas unidades.
Pero ^ ADL esta dado como de 54;40ºº en las mismas unidades (el planeta estuvo en (♏︎ 3 ⅓ - ♎︎ 6º =) 27;20º desde el apogeo en la observación).
Por consiguiente, por sustracción, el ^ ZDL = 31;12ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo ZDX,
arco ZX = 31;12º
y ZX = 32;16p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ = 64;7p (por ej. donde ZL, el radio del epiciclo, es de 22;30p),
XZ = 17;15p.
Y, en el círculo alrededor del triángulo rectángulo ZLX,
donde la hipotenusa ZL = 120p,
ZX ≈ 92p.
En consecuencia arco ZX = 100;8º, [14]
y ^ ZLX = 100;8ºº donde 2 ángulos rectos = 360ºº.
Y demostramos que, en las mismas unidades, ^ ZDL = 31;12ºº,
[por consiguiente ^ ΘZL = ^ ZLX - ^ ZDL = 68;56ºº], y que ^ ΘZK = 3;48ºº.
Por lo tanto, por sustracción [del ^ ΘZK desde el ^ ΘZL],
^ KZL = 65;8 donde 2 ángulos rectos = 360ºº
^ KZL = 32;34 donde 4 ángulos rectos = 360º.
En esta observación, entonces, el planeta estuvo a 32;34º desde K, el perigeo del epiciclo, y, obviamente, a 212;34º desde el apogeo. Pero demostramos que en el momento de nuestra observación estuvo a 99;27º desde el apogeo del epiciclo. Ahora el intervalo entre las dos observaciones es aproximadamente de
402 años Egipcios 283 días y 13 ½ horas.
Este intervalo contiene 1268 vueltas completas del planeta en anomalía (dado que 20 años Egipcios producen bastante [más] por alrededor de 63 vueltas, entonces 400 años producen 1260 [vueltas], y los 2 años restantes más los días adicionales otras 8 vueltas completas). Por lo tanto hemos demostrado que en 402 años Egipcios 283 días 13 ½ horas el planeta Mercurio se movió en anomalía, más allá de 1268 revoluciones completas, [es decir] 246;53º, que es la cantidad por la cual la posición en nuestra observación esta mas allá de la previa. Y justo alrededor del mismo incremento [en anomalía] resultado de las tablas que hemos establecido anteriormente: pues fue [calculado] sobre la base de esos cálculos muy similares donde hicimos nuestra corrección a los movimientos periódicos de Mercurio, reduciendo a días el intervalo arriba [expresado], y a grados las revoluciones en anomalía anteriores mas el incremento. Porque cuando el total de grados esta dividido por el total de días, allí resulta el movimiento medio diario en anomalía que establecimos para Mercurio en nuestra discusión previa (Libro IX Capítulo 3) [15].
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro IX |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 |
Notas de referencia
- ↑ Ver HAMA 165-8.
- ↑ Leer (en los manuscritos D y L) en cambio de ("sus épocas") en H283,4.
- ↑ Literalmente "de la medianoche hacia el 3 er." [día].
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:Elongación de Mercurio en el día de la observación realizada por Ptolomeo Fecha Hora Longitud del Sol Longitud de Mercurio Latitud de Mercurio Elongación Mercurio en Carta 17 de Mayo de 139 d. C. (139) 19:30 hs. ♉︎ 54° 16' 07" ♊︎ 78° 29' 05" +01° 47' 20" E 24° 17' 14" Gemini 
Almagesto Observación 17.05.139 d. C. Hora Puesta del Sol (17/05/139): 18:45:21 hs. Azimut: 112° 57'.
En el atardecer Mercurio se lo puede observar ya a simple vista desde 15 a 30 minutos luego de la puesta del Sol.
Mercurio el 17/05/139 19:30 hs. (Alejandría) Magnitud Fracción Iluminada Altura Azimut +0,3 45,9 % 13° 37' 57" 111° 11' 02" El 17/05/139 a las 19:30 hs. Mercurio se encontraba a 32' 15" (NNE) de Omega Gemini (Mag. +5,18).
Conjunción Luna-Mercurio en el instante de la observación de Ptolomeo (17.05.139 a las 19:30 hs.) Longitud Lunar Latitud Lunar Altura Azimut Fase - Fracción Iluminada Distancia Luna-Mercurio (centro a centro) Luna en Carta ♊︎ 79° 00' 33" -02° 40' 43" 11° 24' 106° 47' Hacia Cuarto Creciente - 5 % 4° 29' 53" (N) Gemini Almagesto Observación 17.05.139 d. C. La máxima elongación de Mercurio ocurrió el 21 de Mayo de 139 d. C. (139) a las 16:08:11 hora local y con una distancia al Este del Sol de 24° 41' 46".
Nota del traductor al español: cartas y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Esas posiciones son calculadas para las 19:42 hs. en Alejandría, por ej. Ptolomeo ha aplicado la Ecuación del Tiempo (Yo encuentro -25 mins. con respecto a la era de Nabonassar). Para este instante los cálculos son muy precisos (encuentro una Paralaje longitudinal de -53' donde Ptolomeo aplica -50').
- ↑ "Perigeo" () aquí y en H285,12 y 14 es tomado, un poco de manera imprecisa, como el punto a 180º desde el apogeo, y no como el punto donde el centro de Mercurio que esta más cerca de la Tierra. Para esto último Ptolomeo siempre utiliza la forma superlativa (H273,11, al.).
- ↑ Cf. Libro IX Capítulo 7 Observaciones [4] y [5] y Libro IX Capítulo 8 Observaciones [Primero] y [Segundo].
- ↑ Este es uno de los casos más raros donde Ptolomeo aplica el equivalente al Teorema del Seno en un triángulo no siendo uno rectángulo. Ver Introducción "(c) Trigonometría", nota de referencia nro. 10.
- ↑ El arco correspondiente a 115;39p es de hecho 149;3º. Pero si uno toma la cuerda como de 115;38,40 (que es una transformación muy precisa de 46;35 * 55;51 / 120), uno lo encuentra como el arco de 149;1,56º. A menudo, Ptolomeo calcula con mayor precisión respecto de lo que visualiza.
- ↑ Ver el catálogo Constelación XXIX Estrellas 2 y 1. Aquí Ptolomeo ha sustraído 4º desde las longitudes para considerar la Precesión de los equinoccios.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Dionysius (actual Atenas) de la siguiente:Elongación de Mercurio en el día de la observación realizada por Dionysius Fecha Hora Longitud del Sol Longitud de Mercurio Latitud de Mercurio Elongación Mercurio en Carta 14 de Noviembre de 265 a. C. (-265) 06:35 hs. ♏︎ (Ophiuchus) 228° 45' 19" ♏︎ 213° 04' 45" +02° 42' 57" W 15° 54' 18" Scorpius 
Almagesto Observación 14.11.265 a. C. Hora Salida del Sol (14/11/-265): 07:05:40 hs. Azimut: 291° 54'.
En el amanecer Mercurio se lo puede observar ya a simple vista desde 15 a 30 minutos antes de la salida del Sol.
Mercurio el 14/11/-265 06:35 hs. (Atenas) Magnitud Fracción Iluminada Altura Azimut +0,9 22,1 % 9° 08' 44" 290° 32' 05" El 14/11/-265 a las 06:35 hs. Mercurio se encontraba a 51' 26" (NNE) de Nu Scorpius (Jabbah, del árabe "la corona en la frente", Mag. +4,01). También en ese instante se encontraba a 2° 04' 43" (ENE) de Beta 1 Scorpius (Acrab 1, "el alacrán", Mag. +2,62), a 2° 27' 52" (NE) de Omega 1 Scorpius (Jabhat al 'Acrab 1, "la frente (del escorpión)", Mag. +3,96) y a 4° 55' 38" (NE) de Delta Scorpius (Dschubba, "la (estrella) delantera de la frente", Mag. +2,3).
La máxima elongación de Mercurio ocurrió el 25 de Noviembre de 265 a. C. (-265) a las 16:37:59 hora local y con una distancia al Oeste del Sol de 22° 14' 14".
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Es muy dificultoso ver como Ptolomeo llega a esta posición desde sus propios datos: ver la discusión en HAMA 166, Fig. 151. Esta fue una observación de una [posición] estacionaria [de Mercurio]. Cf. Ver en el comienzo del Libro IX Capítulo 2 por la descripción de Ptolomeo acerca de las antiguas observaciones.
- ↑ Existe una diferencia adicional (notada por Manitius) de que los significados de los puntos Θ y K han sido intercambiados: en la Fig. 9.9, Θ fue el apogeo medio y K el verdadero, mientras en la Fig. 9.10, K es el perigeo medio y Θ el verdadero.
- ↑ 2;9p podría ser más preciso con cualquier otro método de cálculo.
- ↑ 3;47º podría ser más preciso con cualquier otro método de cálculo.
- ↑ El [valor] más cercano al que uno puede llegar con cualquier método de cálculo es de 100;7º. Cálculos más precisos dan 100;4º.
- ↑ Dado que la presente derivación del movimiento en anomalía ver Cálculos, Ejemplo 16. En la derivación de las dos posiciones en anomalía en las que el movimiento medio, según se basa Ptolomeo, se ha cometido un número erróneo de pequeños cálculos y redondeos. Esto resulta en un error compuesto que no es despreciable, ya que cálculos exactos de sus valores iniciales revelan:
Ptolomeo Cálculos Observación I 212;34º 212;29,18º Observación II 99;27º 99;33,31º Incremento 246;53º 247;4,13º La diferencia de +11', distribuida en aproximadamente 400 años, llega a los +0;0,0,0,16 º/d en el movimiento medio.
