Almagesto: Libro IX - Capítulo 06
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre el tipo y diferencias entre las Hipótesis}
Uno puede comprender más fácilmente el tipo de hipótesis que infiere sobre la base del [fenómeno] precedente según la siguiente descripción.
En primer lugar [elegir] alguno de los [cuatro planetas] distintos de Mercurio, imaginar ABG [Fig. 9.1] la Excéntrica alrededor del centro D, con ADG como diámetro a través de D y [por] el centro de la Eclíptica; sobre esta sea E [el punto] tomado como centro de la eclíptica, por ej. el punto de vista del observador, marcando A el apogeo y G el perigeo. Sea DE bisecado [dividido en dos] en Z, y dibujar un círculo HΘK con centro en Z y radio DA, que debe ser, claramente, igual a ABG. Luego sobre el centro Θ dibujar el Epiciclo LM, y unir LΘMD.
Primero, entonces, asumimos también que el plano de los círculos excéntricos esta inclinado al plano de la eclíptica, y también que el plano del epiciclo esta inclinado al plano de las excéntricas, para tener en cuenta el movimiento latitudinal de los planetas, de acuerdo con lo que hemos de demostrar en relación con este tema, sin embargo, para los movimientos en longitud, en aras de la conveniencia, nos permita [también] imaginar que todos [esos planetas] se ubican en un único [plano], aquel de la eclíptica, dado que no habrá una diferencia longitudinal notable, no al menos cuando las inclinaciones sean tan pequeñas como aquellas que saldrán a la luz para cada uno de los planetas.
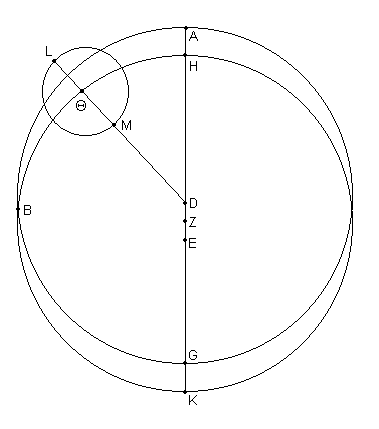
Seguido, decimos que el plano total [de la excéntrica] se mueve uniformemente alrededor del centro E hacia atrás [por ej. del orden] de los signos, cambiando la posición del apogeo y del perigeo 1º cada 100 años, y que el diámetro LΘM del epiciclo gira uniformemente alrededor del centro D, nuevamente hacia atrás [por ej. del orden] de los signos, con una velocidad correspondiente a la vuelta (revolución) del planeta en longitud, y que transporta con él los puntos L y M del epiciclo, y el centro Θ del epiciclo (que siempre se mueve sobre la excéntrica HΘK), y también transporta con él el planeta; el planeta, por su parte, se mueve con movimiento uniforme sobre el epiciclo LM y realiza su vuelta siempre con respecto a aquel diámetro [del epiciclo] el cual apunta hacia el centro D, con una velocidad correspondiente al período medio de la anomalía sinódica, y [un sentido de rotación] tal que su movimiento en el apogeo L tome lugar hacia atrás.
Podemos visualizar las características peculiares de las hipótesis para Mercurio de la siguiente manera. Sea ABG [Fig. 9.2] la excéntrica produciendo la anomalía alrededor del centro D, y sea ADEG el diámetro a través de D y el centro E de la eclíptica, [pasando] a través del apogeo en A. Sobre AG tomar DZ hasta el apogeo A, [siendo] igual a DE. Entonces todo lo demás sigue siendo lo mismo, a saber todo el plano, [girando] alrededor del centro E, desplaza el apogeo hacia atrás por la misma cantidad como para los otros planetas, el epiciclo gira uniformemente alrededor del centro D hacia atrás, como [en este caso] por la línea DB, y además el planeta se mueve sobre el epiciclo en el mismo sentido como los otros. Pero en este caso el centro de la otra excéntrica, que es, nuevamente, igual en tamaño a la primera excéntrica, y sobre la cual el centro del epiciclo esta siempre localizado, es transportado alrededor del punto Z en sentido contrario al movimiento del epiciclo, a saber hacia adelante [por ej. del orden contrario al] de los signos, pero [de manera] uniforme y con la misma velocidad como la del epiciclo, como [en este caso] por la línea ZHΘ.

Por lo tanto en un año cada una de las líneas DB y ZHΘ realizan una vuelta con respecto a un punto [dado] de la eclíptica, pero, obviamente, dos vueltas con respecto a cada uno de los otros. Y [el centro de esta excéntrica] estará siempre a una distancia constante desde el punto Z, y que esta distancia también será igual a ambas ED y DZ ([aquí] como ZH). En consecuencia el pequeño círculo descrito por su movimiento hacia delante, con [su] centro Z y radio ZH, también siempre tiene en su límite el punto D (el centro de la primer, excéntrica fija); y la excéntrica moviéndose, en cualquier momento dado, puede ser descrita con centro H y radio HΘ igual a DA (aquí como ΘK), el epiciclo siempre tendrá su centro sobre él (aquí en el punto K).
Incluso tendremos una comprensión más clara de estas hipótesis desde las demostraciones que haremos [para determinar] los parámetros individualmente para cada planeta. Frecuentemente en estas demostraciones también nos llegarán [a ser] claros, [al menos] a grandes rasgos, los motivos que de alguna manera nos han llevado a adoptar estas hipótesis.
Sin embargo, uno debe realizar la observación preliminar en la que los períodos longitudinales no llevan al planeta a la misma posición tanto con respecto a un punto sobre la eclíptica o [simultáneamente] con respecto al apogeo o al perigeo de la excéntrica; esto se debe al cambio de posición que asignamos a [este] último. Por lo tanto los movimientos medios en longitud que anteriormente hemos tabulado, representan, no las vueltas [de los planetas] definidos con respecto a los apogeos de las excéntricas, sino a las vueltas definidas con respecto a los puntos Solsticiales y Equinocciales, de acuerdo con la longitud del año tal como lo hemos determinado [1].
Ahora, primero debemos probar que a partir de estas hipótesis también continúa que, para iguales distancias del planeta en movimientos medios longitudinales sobre lados opuestos del apogeo y del perigeo, la ecuación de la anomalía eclíptica sobre un lado [del apogeo o del perigeo] es igual a aquella sobre el otro lado, y que la máxima elongación sobre el epiciclo desde la posición media [sobre un lado es igual a aquella] en la misma dirección [sobre el otro lado] [2].
Sea ABGD [Fig. 9.3] el círculo excéntrico sobre el cual se mueve el centro del epiciclo, con centro en E, con diámetro AEG, sobre el cual Z es tomado como centro de la eclíptica, y H como el centro de la excéntrica produciendo la anomalía, por ej. el punto alrededor del cual decimos que toma lugar el movimiento uniforme del epiciclo. Dibujamos BHΘ y DHK a distancias iguales desde el apogeo A (entonces el ^ AHB = ^ AHD), dibujar sobre los puntos B y D los epiciclos de igual tamaño, y unimos BZ y DZ. Desde Z, [siendo] el observador, dibujar ZL y ZM como tangentes a los [2] epiciclos en la misma dirección [por ej. ambos hacia el perigeo].

Digo [1] que los ángulos de la ecuación de la anomalía eclíptica
^ ZBH = ^ HDZ
[2] similarmente, que la máxima elongación sobre el epiciclo
^ BZL = ^ DZM.
(Dado que, [si esas sentencias son verdaderas], las cantidades de las máximas elongaciones desde la [posición] media resultante desde la combinación [de las hipótesis] también serán iguales [sobre los lados opuestos de los Ápsides) [3].
[Demostrar:] Eliminar las perpendiculares BL y DM desde B y D hasta ZL y ZM, y las perpendiculares EN y EX desde E hasta DK y BΘ.
Entonces, dado que el ^ XHE = ^ NHE [4]
y los ángulos en N y X son rectos
y EH es común a los triángulos rectángulos [NHE, XHE],
NH = XH
y la perpendicular EN = perpendicular EX.
Por lo tanto las líneas BΘ y DK son equidistantes desde el centro E.
Por lo tanto ellas son iguales la una con la otra [5],
y sus mitades son iguales una con la otra [por ej. BX = DN].
Por lo tanto, por sustracción [de XH desde BX y NH desde DN],
BH = DH
Pero HZ es común [a los triángulos BHZ, DHZ]
y el ^ BHZ = ^ DHZ [6].
Por lo tanto base BZ = base DZ
y el ^ HBZ = ^ HDZ.
Pero también BL = DM (radio del epiciclo),
y los ángulos en L y M son rectos.
En consecuencia ^ BZL = ^ DZM.
Lo que se ha requerido para examinar.
Nuevamente para representar la hipótesis de Mercurio, sea ABG [Fig. 9.4] el diámetro a través de los centros y del apogeo de los círculos [excéntricos], y sea A tomado como el centro de la eclíptica, B como el centro de la excéntrica produciendo la anomalía, y G como el punto alrededor del cual gira el centro de la excéntrica transportando el epiciclo. Dibujar, nuevamente sobre ambos lados [del apogeo], las líneas BD y BE, representando el movimiento uniforme del epiciclo hacia atrás, y las líneas GZ y GH representando la revolución de la excéntrica hacia adelante con una velocidad igual [a la del epiciclo].

(Entonces esta claro que los ángulos en G y B deben ser iguales, y BD debe ser paralela a GZ, y BE a GH). Sobre GZ y GH tomar los centros de la excéntrica [en movimiento] - sean ellos Θ y K - y sean las excéntricas dibujadas sobre esos centros (sobre los cuales están localizados los epiciclos), [que] pasan a través de los puntos D y E. Sobre los puntos D y E dibujar epiciclos (nuevamente iguales), unir AD y AE, y dibujar AL y AM tangente a los epiciclos sobre el mismo lado [de los epiciclos].
Luego debemos probar que en esta situación [ubicación] también los ángulos de la ecuación [7] de la anomalía eclíptica
^ ADB = ^ AEB,
Y que los ángulos de la máxima elongación sobre el epiciclo
^ DAL = ^ EAM.
[Probar:] Unir BΘ, BK, ΘD y KE,
y eliminar las perpendiculares GN y GX desde G hasta BD y BE,
las perpendiculares DZ y EH desde D y E hasta GZ y GH,
y las perpendiculares DL y EM desde D y E hasta AL y AM.
Entonces, dado que el ^ GBN = ^ GBX [por hipótesis]
y los ángulos en N y X son rectos
y la línea GB es común [a los triángulos GBN, GBX],
GN = GX
por ej. DZ = EH [8].
Y también ΘD = KE [9]
Y los ángulos en Z y H son rectos.
Entonces ^ DΘZ = ^ EKH.
Y porque [en los triángulos GΘB, GKB]
ΘG = GK (por hipótesis)
y GB es común
y ^ ΘGB = ^ KGB,
en consecuencia ^ GΘB = ^ GKB.
Por lo tanto, por sustracción, el ^ BΘD = ^ BKE [10],
y base BD = base BE [11].
Pero nuevamente [en los triángulos BAD, BAE]
BA es común
y ^ DBA = ^ EBA [por hipótesis].
Entonces Base AD = Base AE
y ^ ADB = ^ AEB.
Por el mismo razonamiento [como el anterior]
ya que DL = EM [radio del epiciclo]
y los ángulos en L y en M son rectos
^ DAL = ^ EAM.
Lo que se ha requerido para examinar.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro IX |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 |
Notas de referencia
- ↑ En otras palabras, los movimientos medios tabulados por Ptolomeo son tropicales, no son movimientos medios siderales, y dado que los apogeos son, por su definición, sideralmente fijos, una vuelta en longitud (al mismo punto sobre la eclíptica) debe variar ligeramente [luego] de una vuelta al apogeo.
- ↑ Por "en la misma dirección" significa "ambos hacia el apogeo" o "ambos hacia el perigeo". Esto es explicado por [medio de] la Fig. 9.3., Ptolomeo esta llevando a cabo la prueba de simetría análoga a aquella realizada por los modelos del Sol y de la Luna (Libro III Capítulo 3 Fig. 3.7 y Fig. 3.8).
- ↑ El ^ BZL etc., son las máximas elongaciones verdaderas (vistas desde la Tierra). En lo que sigue, Ptolomeo esta yendo a comparar las máximas elongaciones medias, y esto es esencial para probar que también sean simétricas cerca de la línea de los ápsides. Dado que lo último difiere de los ángulos BZL etc. por un ángulo igual a la ecuación del centro, o al ^ ZBH etc., la simetría esta garantizada por las ecuaciones [1] y [2].
- ↑ Porque ellos están verticalmente opuestos a los ángulos iguales AHB y AHD.
- ↑ Euclides III 14.
- ↑ Eliminar en H259, 4-5. Heiberg enmendó en ([siendo] normal la expresión). Esta [frase] podría significar "los ángulos comprendidos por lados iguales", y fue probablemente interpolada para hacer explícita la condición de Euclides III en I 4, "Si dos triángulos tienen dos lados iguales a [los otros] dos lados, y tienen iguales los ángulos comprendidos por líneas rectas iguales, entonces tendrán la base [de uno] igual a la base [del otro]". La razón por la igualdad de los ángulos es que ellos son [ángulos] suplementarios de los ángulos iguales ^ AHB y ^ AHD.
- ↑ Leer en H260,8, Heiberg, siguiendo el manuscrito Griego, omite la última palabra, que fue restaurada por Halma (seguido por Manitius), aparentemente sin autoridad (firmeza). De hecho fue leído en el manuscrito Is.
- ↑ GZDN y GHEX son paralelogramos.
- ↑ Aunque uno pueda observar que esto debe ser así por simetría, la prueba es verdaderamente intrincada. Porque el radio de la Deferente en sus dos posiciones no son ΘD ni KE, sino KD y ΘE. Cf. Manitius p. 435.
- ↑ El ^ BΘD = 180º - (^ DΘZ + ^ GΘB). El ^ BKE = 180º - (^ EKH + ^ GKB).
- ↑ En los triángulos congruentes BΘD y BKE.