Almagesto: Libro IX - Capítulo 08
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Que el planeta Mercurio, también, llega a su máximo acercamiento a la Tierra dos veces en una Revolución}
De acuerdo con lo anterior, investigamos el tamaño de las Máximas Elongaciones que ocurren cuando la longitud media del Sol esta exactamente en el Apogeo, y nuevamente, cuando esta diametralmente opuesta a ese punto. No podemos derivar esto desde las observaciones más antiguas, sino que podemos hacerlo entonces desde nuestras propias observaciones realizadas con el Astrolabio. Dado que desde estas situaciones [utilizando el instrumento] es en donde uno puede mejor apreciar la utilidad de este modo de hacer las observaciones, ya que, incluso si aquellas estrellas con sus posiciones previamente determinadas, las cuales son visibles, no están tan cerca del planeta siendo observado (generalmente es el caso de Mercurio, ya que, para la mayoría de las Estrellas Fijas, es raro que sean visibles cuando [solamente] están tan lejos del Sol como lo esta Mercurio) [2], [e] incluso uno pueda determinar precisamente las posiciones del planeta en cuestión, en Latitud y en Longitud, observando las estrellas que están a una distancia considerable.
[Primero] entonces, en el decimonoveno año de Adriano, 14/15 de Athyr [III] en el calendario Egipcio [2/3 de Octubre de 134], en el amanecer, Mercurio, estuvo alrededor de su máxima elongación, fue avistado con respecto a la estrella en el corazón de Leo, y observado tener una longitud de ♍︎ 20 ⅕° [3]. La [posición media del] Sol estuvo cerca de ♎︎ 9 ¼º, entonces la máxima elongación fue de 19 1/20º.
[Segundo], en el mismo año, 19 de Pachón [IX] [5 de Abril de 135], por la tarde, [Mercurio], nuevamente estuvo alrededor de su máxima elongación, fue avistado con respecto a la estrella brillante en las Híades, y fue observado tener una longitud de ♉︎ 4 ⅓º [4]. La [posición] media del Sol tuvo una longitud de ♈︎ 11 ½º. Por lo tanto en este caso uno calcula la máxima elongación como de 23 ¼º, e inmediatamente es obvio que el apogeo de la Excéntrica esta en Libra y no en Aries.
Con estos datos, sea ABG [Fig. 9.5] [5] el diámetro a través del apogeo. Sea B tomado como centro de la Eclíptica, en el que esta el observador, A como el punto en ♎︎ 10º, y G como el punto en ♈︎ 10º.
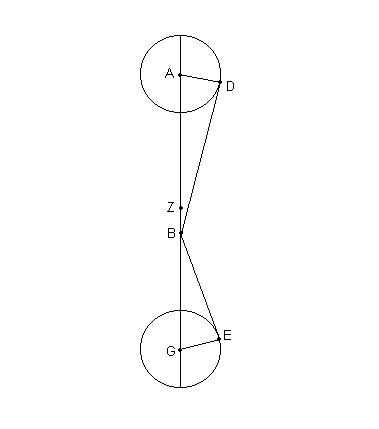
Describir Epiciclos iguales con puntos D y E [sobre sus circunferencias] alrededor de A y de G [respectivamente], y dibujar desde B las tangentes BD y BE hacia ellos. Eliminar las perpendiculares AD y GE desde los centros hasta los puntos de tangencia.
Ahora, dado que la máxima elongación desde la media, como estrella de la mañana en Libra, fue observada de 19 1/20º,
^ ABD = 19;3º donde 4 ángulos rectos = 360º
^ ABD = 38;6ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo en el triángulo rectángulo ABD
arco AD = 38;6º
y sus cuerdas, AD ≈ 39;9p donde la hipotenusa AB = 120p.
Nuevamente, dado que la máxima elongación desde la media, como estrella de la tarde en Aries, fue observada de 23 ¼º,
^ GBE = 23;15º donde 4 ángulos rectos = 360º
^ GBE = 46;30ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto en el círculo alrededor del triángulo rectángulo GBE
arco GE = 46;30º
y su cuerda, GE = 47;22p donde la hipotenusa BG = 120p.
Por lo tanto donde GE = 39;9p y AB = 120p (donde AD = GE, el radio del epiciclo),
BG = 99;9p
y, por adición [de AB a BG], ABG = 219;9p.
Entonces si este esta dividido en el punto Z,
su mitad, AZ = 109;34p (*)
y la distancia entre los puntos B y Z = 10;25p (*)
(*) en las mismas unidades.
Ahora, es claro que ambos, el punto Z es el centro de la excéntrica sobre la cual el centro del epiciclo esta siempre ubicado, o bien el centro de esta [excéntrica] se mueve alrededor del punto Z. Como se ha demostrado, dado que esas son las únicas condiciones en las que el centro del epiciclo podría ser equidistante desde [el punto] Z en ambas de las ubicaciones anteriores diametralmente opuestas. Pero si Z fuera el actual centro de la excéntrica sobre el cual el centro del epiciclo esta siempre localizado, esta excéntrica podría ser estacionaria, y la ubicación en Aries podría ser la mas cercana a la Tierra de todas las situaciones [por ej. el perigeo], dado que BG es la [línea] más corta de [todas] las líneas dibujadas desde B hasta el círculo descrito con centro Z [6]. No obstante, encontramos que la ubicación en Aries no es la más cercana de todas a la Tierra, pero las ubicaciones en Gemini y en Aquarius son incluso las más cercanas a la Tierra con respecto de aquella [(en Aries)], y aproximadamente iguales la una con la otra. Por lo tanto es claro que el centro de la excéntrica en cuestión gira alrededor del punto Z, en el sentido opuesto a la revolución del epiciclo (por ej. hacia delante con respecto de los signos), también haciendo un giro en una revolución [del epiciclo]. Ya que si esto es así, el centro del epiciclo estará mas cerca de la Tierra dos veces [en una revolución] sobre la excéntrica.
En cuanto al hecho de que el epiciclo esta más cerca de la Tierra en Gemini y en Aquarius respecto de la ubicación [anterior] en Aries, fácilmente es visto como una inmediata consecuencia de las observaciones ya detalladas. En la observación en el 16 to. año de Adriano, 16 de Phamenoth (Observación [1], Libro IX Capítulo 7), la máxima elongación desde la media como estrella de la tarde fue de 21 ¼º, y en la observación en el 4 to. año de Antonino Pío, 19 de Phamenoth [7] (Observación [4], Libro IX Capítulo 7), la máxima elongación desde la media como estrella de la mañana fue de 26 ½º, mientras en ambas observaciones [la posición media] del Sol estuvo cerca de ♒︎ 10º. Nuevamente, en la observación del 18 vo. año de Adriano, 19 de Epiphi (Observación [2], Libro IX Capítulo 7), la máxima elongación desde la media como estrella de la mañana fue de 21 ¼º, y en la observación del 1 er. año de Antonino Pío, 20 de Epiphi (Observación [3], Libro IX Capítulo 7), la máxima elongación desde la media como estrella de la tarde fue de 26 ½º, la [posición media] del Sol en ambas de esas observaciones fue alrededor de ♊︎ 10º. Por lo tanto en ambos, en Aquarius y en Gemini, la suma de las máximas elongaciones opuestas llega a [ser] 47 ¾º, mientras la suma de las dos [máximas] elongaciones en Aries es de [solamente] 46 ½º, dado que la elongación de la tarde (es igual a la elongación de la mañana) observada como de 23 ¼º.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro IX |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 |
Notas de referencia
- ↑ Ver HAMA 161, Pedersen 314-15. Por "también" se refiere a la Luna (tomando en cuenta la observación de Ptolomeo al final del Libro IX Capítulo 5). Sobre el término aplicado a Mercurio ver Libro IX Capítulo 10 nota de referencia nro. 5.
- ↑ Dado que la máxima elongación de Mercurio desde el Sol nunca es más de 28º, este [planeta] es visible solamente por un pequeño período de tiempo después de la puesta o antes de la salida del Sol, cuando el cielo en su región esta también iluminado por alguna de las estrellas brillantes visibles. Las "antiguas observaciones" (por ej. aquellas realizadas por lo babilonios o por los antiguos griegos) fueron hechas tomando la posición con respecto a las estrellas cercanas; aunque en algunas regiones de la eclíptica existe una escasez de estrellas brillantes.
- ↑ La estrella tuvo una Longitud de ♌︎ 2 ½º, de acuerdo al catálogo de Ptolomeo (Constelación XXVI Estrella nro. 8), entonces el intervalo observado fue de 47;42º.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:Elongación de Mercurio en el día de la observación realizada por Ptolomeo Fecha Hora Longitud del Sol Longitud de Mercurio Latitud de Mercurio Elongación Mercurio en Carta 2 de Octubre de 134 d. C. (134) 05:25 hs. ♍︎ 187° 32' 55" ♍︎ 169° 25' 32" +02° 03' 42" W 18° 13' 45" Virgo 
Almagesto Observación 02.10.134 d. C. Hora Salida del Sol (02/10/134): 05:54:03 hs. Azimut: 273° 02'.
En el amanecer Mercurio se lo puede observar ya a simple vista desde 15 a 30 minutos antes de la salida del Sol.
Mercurio el 02/10/134 05:25 hs. (Alejandría) Magnitud Fracción Iluminada Altura Azimut -0,7 65,8 % 11° 16' 11" 269° 35' 13" El 02/10/134 a las 05:25 hs. Mercurio se encontraba a 2° 48' 50" (WNW) de Teta Virgo (Ping Taou, del chino "el camino llano o plano", Mag. +4,38)". El 03/10/140 a las 05:25 hs. a 1° 34' 03" (NW).
La máxima elongación de Mercurio ocurrió el 29 de Septiembre de 134 d. C. (134) a las 19:41:26 hora local y con una distancia al Oeste del Sol de 18° 30' 38".
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ La estrella tuvo una longitud de ♌︎ 12 ⅔º, de acuerdo al catálogo (Constelación XXIII Estrella nro. 14), entonces el intervalo observado fue solamente de 8 ⅓º.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:Elongación de Mercurio en el día de la observación realizada por Ptolomeo Fecha Hora Longitud del Sol Longitud de Mercurio Latitud de Mercurio Elongación Mercurio en Carta 5 de Abril de 135 d. C. (135) 18:50 hs. ♈︎ 13° 55' 19" ♉︎ 34° 24' 11" +02° 50' 41" E 20° 40' 14" Taurus 
Almagesto Observación 05.04.135 d. C. Hora Puesta del Sol (05/04/135): 18:19:54 hs. Azimut: 96° 59'.
En el atardecer Mercurio se lo puede observar ya a simple vista desde 15 a 30 minutos luego de la puesta del Sol.
Mercurio el 05/04/135 18:50 hs. (Alejandría) Magnitud Fracción Iluminada Altura Azimut +0,6 32,9 % 13° 32' 47" 100° 28' 56" El 05/04/135 a las 18:50 hs. Mercurio se encontraba a 54' 27" (SSE) de 27-Taurus (Atlas, esposo de Pleione y padre de las Pléyades, Mag. +3,63)".
La máxima elongación de Mercurio ocurrió el 4 de Abril de 135 d. C. (135) a las 03:39:14 hora local y con una distancia al Este del Sol de 20° 46' 53".
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Heiberg ha cometido un error en la figura de la p. 271: Z esta en el lado equivocado de B. Corregido por Manitius.
- ↑ Euclides III 7.
- ↑ Lectura ιθ' (en el manuscrito D y en el Ar) en cambio ιη' (18) en H273,19. Ptolomeo da dos fechas (18/19) en el pasaje en cuestión. Dado que la observación fue realizada en el amanecer, la segunda fecha es la preferible, y esta de acuerdo con la práctica justamente más abajo (19 de Epiphi, temprano en el 18/19, en el amanecer).
