Almagesto: Libro XI - Capítulo 05
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de la Excentricidad de Saturno y [la posición de] su Apogeo}
Para completar este tema, resta demostrar las anomalías y las épocas para la teoría del planeta Saturno. Una vez más, como para [todos] los otros planetas, tomamos, primero, para nuestra investigación de [la posición del] apogeo y de la excentricidad, tres ubicaciones del planeta en su oposición, en las que este estuvo diametralmente opuesto a la posición media [en longitud] del Sol.
[1] La primera de ellas fue observada por nosotros, utilizando los instrumentos astrolabios, en el decimoprimer año de Adriano, 7/8 de Pachón [IX] en el calendario Egipcio [26/27 de Marzo de 127], por la tarde, [ubicado] en ♎︎ 1;13º [1];
[2] la segunda, en el decimoséptimo año de Adriano, 18 de Epiphi [XI] en el calendario Egipcio [3 de Junio de 133]. Calculamos exactamente el tiempo y la ubicación del [planeta en su] oposición desde observaciones cercanas [resultando tal oposición] 4 horas después del mediodía del 18 avo. [día de Epiphi], en ♐︎ 9;40º [2];
[3] observamos la tercera oposición en el vigésimo año de Adriano, 24 de Mesore [XII] en el calendario Egipcio [8 de Julio de 136]. Como antes, calculamos el tiempo exacto de la oposición precisamente habiendo ocurrido al mediodía en el 24 to. [día de Mesore], y calculado la ubicación en ♑︎ 14;14º [3].
Entonces, de estos dos intervalos, aquel desde la primera hasta la segunda oposición comprende
| [en tiempo] | 6 años Egipcios 70 días 22 horas |
| en movimiento aparente del planeta | 68;27º |
mientras que desde la segunda hasta la tercera oposición comprende
| [en tiempo] | 3 años Egipcios 35 días 20 horas |
| [en movimiento aparente] | 34;34º |
Y calculamos para el movimiento medio en longitud, utilizando cifras aproximadas [4]
| para el primer intervalo: | 75;43º |
| y para el segundo intervalo: | 37;52º |
Siendo dados estos intervalos [en longitud media y verdadera], de la siguiente manera nuevamente demostramos los [parámetros] requeridos por medio del mismo teorema [como el de antes] (como si hubiera solo una Excéntrica).
Para evitar la repetición, sea dibujado un diagrama [Fig. 11.12] como aquellos utilizados para la misma demostración [previamente, en las Fig. 10.8 y Fig. 11.1. Entonces dado que el arco BG de la excéntrica esta dado como subtendiendo 34;34º de la Eclíptica, el ángulo [correspondiente] en el centro de la eclíptica [es],
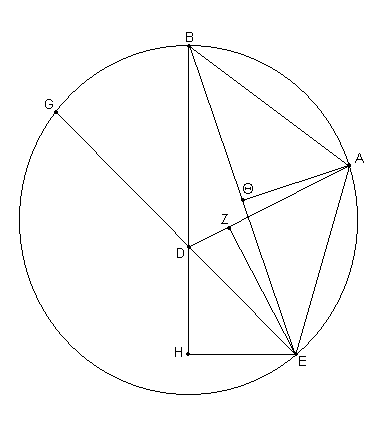
el ^ BDG (= ^ EDH) = 34;34º donde los 4 ángulos rectos = 360º
el ^ BDG (= ^ EDH) = 69;8ºº donde los 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DEH,
arco EH = 69;8º
y EH = 68;5p donde la hipotenusa DE = 120p.
Similarmente, ya que el arco BG = 37;52º, el ángulo en la circunferencia,
el ^ BEG = 37;52ºº donde los 2 ángulos rectos = 360ºº,
y, por sustracción [desde el ^ BDG], ^ EBH = 31;16ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo EBH,
arco EH = 31;16º
y EH = 32;20p donde la hipotenusa BE = 120p.
Por lo tanto donde EH, como demostramos, es 68;5p, y ED = 120p,
EB = 252;41p.
Además, dado que todo el arco ABG subtiende 103;1º de la eclíptica (la suma de ambos intervalos [en longitud verdadera]), el ángulo [correspondiente] en el centro de la eclíptica,
[es] el ^ ADG = 103;1º donde 4 ángulos rectos = 360º.
Por lo tanto el ángulo suplementario, ^ ADE = 76;59º en las mismas unidades
Por lo tanto el ángulo suplementario, ^ ADE = 153;58ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DEZ,
arco EZ = 153;58º
y EZ = 116;55p donde la hipotenusa DE = 120p.
Similarmente, dado que el arco ABG de la excéntrica es hallado por la suma [de 75;43º con 37;52º] como de 113;35º, el ángulo en la circunferencia,
el ^ AEG = 113;35ºº donde 2 ángulos rectos = 360ºº.
Pero encontramos que el ^ ADE = 153;58ºº en las mismas unidades.
Por lo tanto el ángulo restante [en el triángulo ADE],
el ^ ZAE = 92;27ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AEZ,
arco EZ = 92;27º
y EZ = 86;39p donde la hipotenusa AE = 120p.
Por lo tanto donde EZ, como demostramos, es de 116;55p, y ED = 120p
EA = 161;55p.
Además, ya que el arco AB de la excéntrica es de 75;43º, el ángulo en la circunferencia
el ^ AEB = 75;43ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AEΘ,
arco AΘ = 75;43º,
y arco EΘ = 104;17º (suplementario).
Por lo tanto las cuerdas correspondientes
AΘ = 73;39p donde la hipotenusa EA = 120p
y EΘ = 94;45p donde la hipotenusa EA = 120p.
Por lo tanto donde AE, fue demostrado, ser de 161;55p, y DE = 120p,
AΘ = 99;23p [5]
y EΘ = 127;51p.
Pero demostramos que toda la línea total EB = 252;41p en las mismas unidades. Por lo tanto, por sustracción, ΘB = 124;50p donde AΘ= 99;23p.
Y ΘB² = 15583;22
y AΘ² = 9877;3
y ΘB² + AΘ² = AB² = 25460;25.
En consecuencia AB = 159;34p donde ED = 120p y EA = 161;55p.
Y, donde el diámetro de la excéntrica es de 120p, AB = 73;39p
(dado que este subtiende un arco de 75;43º).
Por lo tanto donde AB = 73;39p y el diámetro de la Excéntrica es de 120p,
ED = 55;23p
y EA = 74;43p.
Por lo tanto el arco EA de la excéntrica = 77;1º
y, por la suma [del arco ABG], el arco EABG = 190;36º,
y por consiguiente, por sustracción [dado el círculo], el arco GE = 169;24º.
Por lo tanto GDE ≈ 119;28p donde le diámetro de la excéntrica es de 120p.
Entonces, [ver Fig. 11.13] sea el centro de la excéntrica tomado dentro del segmento EAG (dado que este es mayor que un semicírculo) como punto K. Dibujar a través de K y D el diámetro de la excéntrica a través de ambos centros, LKDM, y sea la perpendicular desde K hasta GE prolongada como KNX [hasta encontrar la circunferencia] .
Entonces, donde el diámetro, LM = 120p,
toda la línea EG fue demostrada ser de 119;28p y ED ser de 55;23p;
entonces, por sustracción, DG = 64;5p en las mismas unidades.
Entonces, dado que ED * DG = LD * DM,
LD * DM = 3549;9p donde el diámetro LM es de 120p.
Pero LD * DM + DK² = LK² (el cuadrado de la mitad del diámetro).

Por lo tanto, si desde el cuadrado de la mitad del diámetro, [igual a] 3600, sustraemos 3549;9, y nos queda con DK² como de 56;51p en las mismas unidades.
Por lo tanto la distancia entre los centros, DK ≈ 7;8p
donde el diámetro de la excéntrica es de 120p [6].
Además, ya que EN (= ½ * GE) = 59;44p donde el diámetro LM = 120p,
y demostramos que ED = 55;23p en las mismas unidades,
por sustracción, DN = 4;21p donde DK, como mostramos, = 7;8p.
Por lo tanto donde la hipotenusa [del triángulo rectángulo DKN] DK = 120p,
DN = 73;11p,
y, en el círculo alrededor del triángulo rectángulo DKN
arco DN = 75;10º.
En consecuencia el ^ DKN = 75;10ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ DKN = 37;35º donde 4 ángulos rectos = 360º.
Y dado que el ^ DKN es un ángulo en el centro de la excéntrica,
arco XM = 37;35º [7].
Pero el arco GX = ½ * arco GXE = 84;42º.
Por lo tanto, por sustracción [del (arco GX + arco XM) desde los 180º], el arco desde el apogeo hasta la tercera oposición,
arco GL = 57;43º.
Pero el arco BG esta dado como de 37;52º.
Por lo tanto, por sustracción, el arco desde el apogeo hasta la segunda oposición,
arco LB = 19;51º.
Similarmente, dado que el arco AB esta dado como de 75;43º,
por sustracción, el arco desde la primera oposición hasta el apogeo,
arco AL = 55;52º.
Ahora nuevamente, dado que el centro del Epiciclo es transportado, no sobre esta excéntrica, sino sobre aquella dibujada con centro en el punto bisecando [(dividiendo en dos a)] DK y con el radio KL, calculamos en debido orden, como lo hicimos para [todos] los otros [planetas], las diferencias en los intervalos aparentes [en longitud verdadera] sobre la eclíptica que resulta desde las proporciones anteriores (tomándolas hasta ser aproximadamente las correctas), si transferimos la "ruta" del epiciclo hasta la excéntrica en cuestión, la cual produce la anomalía eclíptica (por ej. la Ecuante).
Por consiguiente, sea allí dibujado [Fig. 11.14] el diagrama para la primera oposición, [similar al previo] en la misma demostración, pero dibujado hacia adelante del apogeo L. Entonces, dado que el ángulo de la posición media en longitud,
el ^ NZX (= ^ DZH) = 55;52º donde 4 ángulos rectos = 360º
el ^ NZX (= ^ DZH) = 111;44ºº donde 2 ángulos rectos = 360ºº,
en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 111;44º
y arco ZH = 68;16º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 99;20p donde la hipotenusa DZ = 120p
y ZH = 67;20p donde la hipotenusa DZ = 120p.
Por lo tanto donde la distancia entre los centros, DZ = 3;34p,
y el radio de la excéntrica, DA = 60p,
DH = 2;57p
y ZH = 2;0p.
Y dado que DA² - DH² = AH²,
AH = 59;56p en las mismas unidades.
Similarmente, dado que ZH = ΘH,
y ΘE = 2 * DH,
Y por adición, AΘ = 61;56p donde EΘ = 5;54p.

Por lo tanto la hipotenusa [del triángulo rectángulo ΘAE]
AE = 62;13p en las mismas unidades.
Por lo tanto, donde la hipotenusa AE = 120p, EΘ = 11;21p [8],
y, en el círculo alrededor del triángulo rectángulo AEΘ,
arco EΘ ≈ 10;51º
en consecuencia el ^ EAΘ = 10;51ºº donde 2 ángulos rectos = 360ºº.
Además, donde EΘ = 5;54p,
y el radio de la excéntrica, ZX = 60p, y ZΘ = 4p;
por consiguiente, por adición, ΘX, obviamente, = 64p,
y tomamos la hipotenusa [del triángulo rectángulo EΘX]
EX como de 64;16p en las mismas unidades.
Por lo tanto, donde la hipotenusa EX = 120p, ΘE = 11;2p,
y, en el círculo alrededor del triángulo rectángulo EΘX,
arco ΘE = 10;33º.
En consecuencia el ^ EXΘ = 10;33ºº donde 2 ángulos rectos = 360ºº.
Pero demostramos que el ^ EAΘ = 10;51ºº en las mismas unidades.
Por lo tanto, por sustracción, el ángulo de la diferencia requerida,
el ^ AEX = 0;18ºº donde 2 ángulos rectos = 360ºº
el ^ AEX = 0;9º donde 4 ángulos rectos = 360º.
Pero el planeta en la primera oposición, cuando [fue] visto a lo largo de la línea AE, tuvo una longitud aparente de ♎︎ 1;13º. Por lo tanto, esta claro que si el centro del epiciclo fue transportado, no sobre AL, sino sobre NX, este podría haber estado en el punto X [en la primera oposición], y el planeta podría haber sido visto a lo largo de la línea EX, 9' hacia delante de su [actual] posición en A, con una longitud de ♎︎ 1;4º.
Nuevamente, sea allí dibujado [Fig. 11.15] el diagrama para la segunda oposición, [como aquella] en la misma demostración [previa], pero dibujada hacia atrás del apogeo. [Entonces,] dado que el arco NX de la excéntrica fue demostrado ser de 19;51º,
el ^ NZX = ^ DZH (verticalmente opuesto) = 19;51º donde 4 ángulos rectos = 360º
el ^ NZX = ^ DZH (verticalmente opuesto) = 39;42ºº donde 2 ángulos rectos = 360ºº.
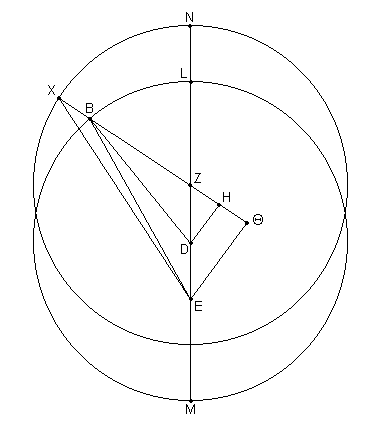
Por lo tanto, en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 39;42º
y arco ZH = 140;18º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 40;45p donde la hipotenusa DZ = 120p
y ZH = 112;52p donde la hipotenusa DZ = 120p.
Por lo tanto, donde DZ = 3;34p y el radio de la excéntrica, DB = 60p,
DH = 1;13p
y ZH = 3;21p.
Y, dado que DB² - DH² = BH²,
BH ≈ 59;59p en las mismas unidades.
Similarmente, dado que ZH = HΘ, y EΘ = 2 * DH,
por adición, BΘ = 63;20p donde EΘ = 2;26p.
Por consiguiente la hipotenusa [del triángulo rectángulo BEΘ]
EB = 63;23p en las mismas unidades.
Por lo tanto donde la hipotenusa BE = 120p, EΘ = 4;36p, y, en el círculo alrededor del triángulo rectángulo BEΘ,
arco EΘ = 4;24º
en consecuencia el ^ EBΘ = 4;24ºº donde 2 ángulos rectos = 360ºº.
Asimismo, donde el radio de la excéntrica, XZ = 60p,
ZΘ es calculado como 6;42p;
entonces, por adición, XΘ = 66;42p donde EΘ es dado como de 2;26p.
Por lo tanto encontramos la hipotenusa [del triángulo rectángulo EΘX] EX como de 66;45p en las mismas unidades.
Por lo tanto, donde la hipotenusa EX = 120p, EΘ = 4;23p,
y, en el círculo alrededor del triángulo rectángulo EΘX,
arco EΘ = 4;12º.
En consecuencia el ^ EXΘ = 4;12ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ EBΘ fue demostrado ser de 4;24ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ BEX = 0;12ºº en las mismas unidades
Por lo tanto, por sustracción, el ^ BEX = 0;6º donde 4 ángulos rectos = 360ºº.
Entonces, aquí también esta claro, dado que el planeta en la segunda oposición, cuando [fue] visto a lo largo de EB, tuvo una longitud de ♐︎ 9;40º, que si, en cambio, este fuera visto a lo largo de EX, este podría [haber] tenido una longitud de ♐︎ 9;46º. Y demostramos, sobre la misma hipótesis, que en la primera oposición este [también] podría haber tenido una longitud de ♎︎ 1;4º.
Por lo tanto, esta claro que el intervalo, en [longitud] aparente, desde la primera hasta la segunda oposición, si este fuera tomado con respecto a la excéntrica NX, podría ser de 68;42º de la eclíptica.
Sea dibujado el diagrama para la tercera oposición [Fig. 11.16], con el mismo diseño como aquel que establecimos anteriormente para la segunda. [Entonces,] dado que demostramos [luego Fig. 11.13] que el arco NX = 57;43º,

el ^ NZX (= ^ DZH) = 57;43º donde 4 ángulos rectos = 360º
el ^ NZX (= ^ DZH) = 115;26ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 115;26º
y arco ZH = 64;34º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 101;27p donde la hipotenusa DZ = 120p
y ZH = 64;6p donde la hipotenusa DZ = 120p.
Por lo tanto donde DZ = 3;34p y el radio de la excéntrica, DG = 60p,
DH = 3;1p
y ZH = 1;54p.
Nuevamente, dado que DG² - DH² = GH²,
GH = 59;56p en las mismas unidades.
Similarmente, dado que ZH = ΘH, y EΘ = 2 * DH,
[y] por suma, GΘ = 61;50p donde EΘ es calculado como de 6;2p;
Por lo tanto la hipotenusa [del triángulo rectángulo GEΘ]
EG = 62;8p en las mismas unidades.
Por lo tanto, donde la hipotenusa GE = 120p, EΘ = 11;39p,
y, en el círculo en el triángulo rectángulo GEΘ,
arco EΘ ≈ 11;9º.
En consecuencia el ^ EGΘ = 11;9ºº donde 2 ángulos rectos = 360ºº.
Similarmente, donde el radio de la excéntrica, XZ = 60p,
ZΘ es calculada como de 3;48p;
entonces, por suma, XΘ = 63;48p donde EΘ fue encontrada ser de 6;2p.
Por lo tanto la hipotenusa [del triángulo rectángulo EΘX]
EX = 64;5p en las mismas unidades.
Por lo tanto, donde la hipotenusa EX = 120p, EΘ = 11;18p,
y, en el círculo alrededor del triángulo rectángulo EΘX,
arco EΘ = 10;49º
en consecuencia el ^ EXΘ = 10;49ºº donde 2 ángulos rectos = 360ºº.
Pero demostramos que el ^ EGΘ = 11;9ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ GEX = 0;20ºº en las mismas unidades
Por lo tanto, por sustracción, el ^ GEX = 0;10º donde 4 ángulos rectos = 360º.
Por consiguiente, dado que el planeta en la tercera oposición, cuando fue observado a lo largo de la línea EG, tuvo una longitud de ♑︎ 14;14º, esta claro que, si este ha estado sobre la línea EX, podría haber tenido una longitud de ♑︎ 14;24º, y el intervalo desde la segunda oposición hasta la tercera en [longitud] aparente, tomada con respecto a la excéntrica NX, podría haber estado (♑︎ 14;24º - ♐︎ 9;46º =) 34;38º.
Entonces, empezando desde esos intervalos continuamos a través del mismo teorema, y encontramos la distancia entre los centros de la eclíptica y de la excéntrica que producen el movimiento uniforme del epiciclo (por ej. la distancia igual hasta EZ [en la Fig. 11.16]) como alrededor de 6;50p donde el diámetro de la excéntrica es de 120p, y [los valores siguientes] para los arcos de esta misma excéntrica:
| desde la primera oposición hasta el apogeo | 57;5º |
| desde el apogeo hasta la segunda oposición | 18;38º |
| desde el apogeo hasta la tercera oposición | 56;30º |
Nuevamente aquí, las cantidades anteriores han sido derivadas precisamente por este método; dado que las diferencias en los arcos eclípticos calculados desde estos arcos son casi los mismos como los del conjunto previo [9], y los intervalos aparentes [en longitud] del planeta son encontrados estar de acuerdo con aquellos observados, como demostraremos por un procedimiento similar [a los precedentes de Júpiter y Marte].
Sea dibujado el diagrama [Fig. 11.17] para la primera oposición, con solamente con la excéntrica transportando el centro del epiciclo. Luego, dado el ángulo subtendiendo 57;5º de la excéntrica [por ej. la ecuante],
el ^ AZL = 57;5º donde 4 ángulos rectos = 360º,
y el ^ AZL = ^ DZH (verticalmente opuesto) = 114;10ºº donde 2 ángulos rectos = 360ºº,

en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 114;10º
y arco ZH = 65;50º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 100;44p donde la hipotenusa DZ = 120p
y ZH = 65;13p donde la hipotenusa DZ = 120p.
Por lo tanto donde la distancia entre los centros, DZ = 3;25p, y el radio de la excéntrica, DA = 60p,
DH = 2;52p
y ZH = 1;51p.
Además, dado que AD² - DH² = AH²,
AH = 59;56p en las mismas unidades.
Similarmente, dado que ZH = HΘ, y EΘ = 2 * DH,
Por adición, AΘ = 61;47p donde EΘ es calculado como de 5;44p.
Por consiguiente la hipotenusa [del triángulo rectángulo AEΘ]
AE = 62;3p en las mismas unidades.
Por lo tanto, donde la hipotenusa AE = 120p, EΘ = 11;5p,
y, en el círculo alrededor del triángulo rectángulo AEΘ,
arco EΘ = 10;36º.
En consecuencia el ^ EAZ = 10;36ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ AZL fue dado como de 114;10ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ AEL = 103;34ºº en las mismas unidades
Por lo tanto, por sustracción, el ^ AEL = 51;47º donde 4 ángulos rectos = 360º.
Entonces, estos [51;47º], fue la cantidad por la cuál el planeta estuvo hacia delante del apogeo en la primera oposición.
Nuevamente, sea dibujado de la misma manera el diagrama [Fig. 11.18] para la segunda oposición.

[Entonces,] ya que el ^ BZL fue demostrado ser de 18;38º donde 4 ángulos rectos = 360º,
y el ^ BZL = ^ DZH (verticalmente opuesto) = 37;16ºº donde 2 ángulos rectos = 360º,
en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 37;16º
y arco ZH = 142;44º (suplementario).
Por lo tanto las cuerdas correspondientes
DH = 38;20p donde la hipotenusa DZ = 120p
y ZH = 113;43p donde la hipotenusa DZ = 120p.
Entonces donde DZ = 3;25p y el radio de la excéntrica, DB = 60p,
DH = 1;5p
y ZH = 3;14p.
Y dado que DB² - DH² = BH²,
BH = 59;59p en las mismas unidades.
Similarmente, ya que ZH = HΘ, y EΘ = 2 * DH,
por suma, BΘ = 63;13p donde EΘ esta calculado como de 2;10p.
Por consiguiente la hipotenusa [del triángulo rectángulo BEΘ]
EB = 63;15p en las mismas unidades.
Por lo tanto, donde la hipotenusa EB = 120p, ΘE = 4;7p,
y, en el círculo alrededor del triángulo rectángulo BEΘ,
arco ΘE = 3;56º.
En consecuencia el ^ EBZ = 3;56ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ BZL fue dado como de 37;16ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ BEL = 33;20ºº en las mismas unidades
Por lo tanto, por sustracción, el ^ BEL = 16;40º donde 4 ángulos rectos = 360º.
Por lo tanto en la segunda oposición la posición aparente del planeta estuvo 16;40º hacia atrás del apogeo. Y demostramos que en la primera oposición este estuvo a 51;47º hacia delante del mismo apogeo. Por lo tanto, el intervalo en [longitud] aparente desde la primera oposición hasta la segunda esta calculada como la suma de las cantidades arriba [descritas], [siendo de] 68;27º, de acuerdo con la distancia encontrada desde las observaciones [Fig. 11.12].
Ahora sea dibujado el diagrama para la tercera oposición [Fig. 11.19]. [Entonces,] dado que
el ^ GZL fue demostrado ser de 56;30º donde 4 ángulos rectos = 360º,
y el ^ GZL = ^ DZH (verticalmente opuesto) = 113;0ºº donde 2 ángulos rectos = 360ºº, en el círculo alrededor del triángulo rectángulo DZH,
arco DH = 113º
y arco ZH = 67º (suplementario).
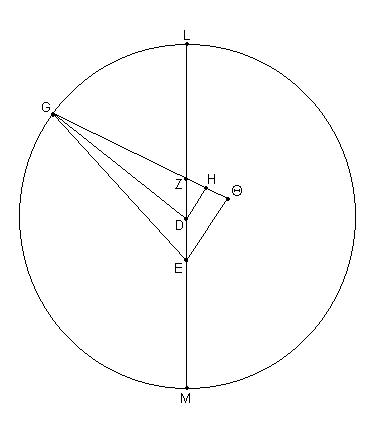
Por lo tanto las cuerdas correspondientes
DH = 100;4p donde la hipotenusa DZ = 120p
y ZH = 66;14p donde la hipotenusa DZ = 120p.
Por lo tanto, donde DZ = 3;25p, y el radio de la excéntrica, DG = 60p,
DH = 2;51p
y ZH = 1;53p.
Nuevamente, dado que DG² - DH² = GH²,
GH = 59;56p en las mismas unidades.
Similarmente, dado que ZH = HΘ, y EΘ = 2 * DH,
por adición, GΘ = 61;49p donde EΘ es calculado como de 5;42p;
por consiguiente la hipotenusa [del triángulo rectángulo GEΘ]
EG = 62;5p en las mismas unidades.
Por lo tanto, donde la hipotenusa GE = 120p; EΘ = 11;1p [10]
y, en el círculo alrededor del triángulo rectángulo GEΘ,
arco EΘ = 10;32º
en consecuencia el ^ EGΘ = 10;32ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ GZL fue dado [11] como de 113ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ GEL = 102;28ºº en las mismas unidades
Por lo tanto, por sustracción, el ^ GEL = 51;14 donde 4 ángulos rectos = 360º.
Entonces, estos [51;14º], es la cantidad por la cuál el planeta estuvo hacia atrás del apogeo en la tercera oposición. Y demostramos que en la segunda oposición este estuvo 16;40º hacia atrás del mismo apogeo. Entonces la distancia en [longitud] aparente desde la segunda oposición hasta la tercera es calculada como la diferencia [entre 51;14º y 16;40º], [siendo igual a] 34;34º, que esta, nuevamente, de acuerdo con aquella derivada de las observaciones [Fig. 11.12].
Inmediatamente esto esta claro, dado que el planeta en la tercera oposición tuvo una longitud de ♑︎ 14;14º, y fue demostrada ser de 51;14º hacia atrás del apogeo, tanto que el apogeo de su excéntrica tuvo en aquel momento una longitud de ♏︎ 23º, mientras su perigeo estuvo diametralmente opuesto a ♉︎ 23º.
Por el mismo camino [como el de antes], si dibujamos [Fig. 11.20] el epiciclo HΘ alrededor del centro G, inmediatamente tomamos la posición media en longitud del epiciclo desde el apogeo de la excéntrica como de 56;30º (demostrada [luego de la Fig. 11.16]), y el arco ΘK del epiciclo como de 5;16º (dado que el ^ EDZ que fue demostrado [anteriormente] ser de 10;32ºº donde 2 ángulos rectos es igual a 360ºº). Por lo tanto, por sustracción [desde los 180º],
el arco HΘ, desde el apogeo del epiciclo del planeta, es de 174;44º. Por lo tanto en el instante de la tercera oposición, a saber en el vigésimo año de Adriano, 24 de Mesore en el calendario Egipcio, al mediodía, el planeta Saturno tuvo las siguientes posiciones medias:
| en longitud: | 56;30º desde el apogeo de la excéntrica (por ej. su longitud [media] fue de ♑︎ 19;30º); |
| en anomalía: | 174;44º desde el apogeo del epiciclo. |
Lo que se ha requerido para examinar.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XI |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
Notas de referencia
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
En ese instante, Saturno se encontraba a: 5° 47' 55" (WNW) de Kapa Virgo y a 6° 42' 34" (WSW) de Iota Virgo (Syrma, del árabe "el tren, o arreo") .
La oposición de Saturno ocurrió el 25 de Marzo de 127 d. C. (127) a las 05:44:47 hora local. Ese mismo día pasaba por el meridiano del lugar a las 00:12:20 hs., altura: 60° 18' y azimut: 0°. Distancia Tierra-Saturno: 1.325.437.128,20 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
En ese instante, Saturno se encontraba a: 3° 19' 52" (NNE) de Lambda Sagittarius (Kaus Borealis, del latín "la parte Norte del arco").
La oposición de Saturno ocurrió el 3 de Junio de 133 d. C. (133) a las 20:43:14 hora local. Ese mismo día pasaba por el meridiano del lugar a las 23:53:50 hs., altura: 37° 43' y azimut: 0°. Distancia Tierra-Saturno: 1.359.844.638,30 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
En ese instante, Saturno se encontraba a: 2° 23' 37" (W) de Theta Capricornius y a 3° 48' 26" de Upsilon Capricornius (Loo Sieu, del chino "el cinto o cordón").
La oposición de Saturno ocurrió el 9 de Julio de 136 d. C. (136) a las 14:30:37 hora local. Ese mismo día pasaba por el meridiano del lugar a las 00:03:47 hs., altura: 35° 36' y azimut: 0°. Distancia Tierra-Saturno: 1.329.925.064,30 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Aquí, a pesar de la frase de Ptolomeo, los intervalos en longitud media son [tan] precisos al minuto más cercano de acuerdo a sus propias tablas. Tampoco la Ecuación del Tiempo podría hacer alguna diferencia.
- ↑ Leer seg. en cambio de seg. (99;43p) en H396,10 y en H396,13. "23", que esta garantizado [(validado)] en el resto del trabajo de Ptolomeo, es encontrado en el manuscrito de Ger (Gerardo de Cremona).
- ↑ DG y ED han sido calculados solo con pequeñas imprecisiones (encuentro 64;5,21p y 55;23,39p para los [valores] de Ptolomeo de 64;5p y 55;23p), aunque el valor resultante para la excéntrica, 7;3,33p, difiere significativamente del [valor de] 7;8p de Ptolomeo.
- ↑ Nuevamente, la acumulación de pequeños errores llegan a una diferencia significante de 38;1º, entre el resultado de Ptolomeo y el valor calculado [de modo] preciso.
- ↑ Yo encuentro 11;23p, derivando a un arco EΘ = 10;53º.
- ↑ Incluso, con una iteración más, uno encuentra correcciones de 0;9,28º, 0;5,36º y de 0;9,40º (comparar con los de Ptolomeo: 9', 6' y 10'), y un resultado para la excentricidad y para el apogeo casi de acuerdo con aquello adoptado por Ptolomeo.
- ↑ Leer seg. seg. (en el manuscrito Ar) en cambio de seg. seg. (11;10p) en H411,22. La lectura es confirmada por los cálculos involucrados.
- ↑ Leer , en el manuscrito D, en cambio de ("es dado") en H 412,1.


