Almagesto: Libro XII - Capítulo 05
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de los [Movimientos] Retrógrados de Venus}
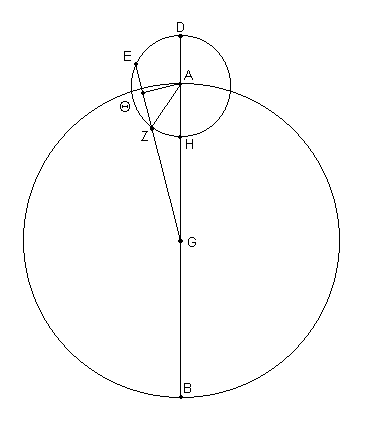
Nuevamente, en el caso del planeta Venus [ver Fig. 12.11], de acuerdo a nuestros cálculos para la distancia media,
ΘZ / ZG = 1 / 0;37,31 [1],
EG / GZ = 2;37,31 / 0;37,31,
y EG * GZ = 1;38,30.
Además, GA / AH = 60 / 43;10,
DG / GH = 103;10 / 16;50,
y DG * GH = 1736;38,20.
Dividiendo [1736;38,20 por 1;38,30], obtenemos 1057;51 [2], cuya raíz cuadrada, es de 32;31,29, [y] multiplicado por la proporción de arriba de ΘZ / ZG, da, en términos de los tamaños anteriores de GA y AZ, [por ej. 60 y 43;10],
ΘZ = 32;31,29p,
GZ = 20;20,11p en las mismas unidades,
y, por suma, GΘ = 52;51,40p.
Por consiguiente, donde las hipotenusas AZ y AG son cada una de 120p [respectivamente],
ZΘ = 90;24,58p
y GΘ = 105;43,20p.
Los arcos [correspondientes] son:
arco ZΘ = 97;47,0º
y arco GΘ = 123;31,49º.
Por consiguiente el ^ ZAΘ = 48;53,30º
y el ^ GAΘ ≈ 61;45,54º.
Y, por sustracción, el ^ ZGA, que representa la [cantidad del movimiento] Retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 28;14,6º, mientras el ^ ZAH, que representa el [movimiento] de la anomalía [media], es de [^ GAΘ - ^ ZAΘ =] 12;52,24º. A este último le corresponde un movimiento [medio] en longitud de 20;35,19º [3], de acuerdo a la proporción media anterior [de las velocidades], y
| la mitad del [movimiento] retrógrado es calculado ser de | [28;14,6º - 20;35,19º =] 7;38,47º y alrededor de 20 ⅚ días. |
| Y el [movimiento] retrógrado total es de | 15;17,34º y 41 ⅔ días. |
[Por consiguiente] la distancia en la Elongación de las [posiciones] estacionarias desde el apogeo y el perigeo es, [respectivamente,] de alrededor de 0;5p de la distancia media [por ej. 60p] menor que la máxima distancia, y de alrededor de la misma cantidad mayor que la mínima distancia [4].
De acuerdo a nuestros cálculos dado que cerca de la máxima distancia, la ecuación [correspondiente a 1º] para las correcciones [de las velocidades], es hallada ser de 2 ⅓' [5]. Por consiguiente
ΘZ / ZG = 0;57;40 / 0;39,51,
EG / GZ = 2;35,11 / 0;39,51,
y EG * GZ = 1;43,4.
Además GA / AH = 61;10 / 43;10,
DG / HG = 104;20 / 18;0,
y DG * HG = 1878;0.
Dividiendo [1878 por 1;43,4], nos da 1093;16,23, cuya raíz cuadrada es, 33;3,53, multiplicada por la proporción ΘZ / ZG, da, en términos de los tamaños anteriores de GA y AZ [por ej. 61;10 y 43;10],
ΘZ = 31;46,44p,
GZ = 21;57,38p en las mismas unidades,
y, por suma, GΘ = 53;44,22p.
Por consiguiente, donde las hipotenusas AZ y AG son cada una de 120p [respectivamente],
ZΘ = 88;20,34p
y GΘ = 105;25,44p.
Los arcos [correspondientes] son:
arco ZΘ = 94;48,54º
y arco GΘ = 122;56,27º.
De acuerdo con el ^ ZAΘ = 47;24,27º
y el ^ GAΘ = 61;28,14º.
Y, por sustracción, el ^ ZGA, que representa la [cantidad del movimiento] retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 28;31,46º, mientras el ^ ZAH, que representa el [movimiento en] anomalía aparente, es de [^ GAΘ - ^ ZAΘ =] 14;3,47º. A esto último le corresponden [movimientos de] 20;19,3º, en longitud corregida y 21;9,3º en longitud media, de acuerdo a las proporciones [de las velocidades] en el apogeo [6]. Por lo tanto
| la mitad del [movimiento] retrógrado llega a | [28;31,46º - 20;19,3º =] 8;12,43º y alrededor de 21 ½ días. |
| El [movimiento] retrógrado total es de | 16;25,26º y 43 días. |
De acuerdo a nuestros cálculos dado que cerca de la mínima distancia, la ecuación [correspondiente a un argumento de 1º] para la corrección de [las velocidades] es hallada ser por la misma cantidad de, 2 ⅓' [7]. Por consiguiente
ZΘ / ZG = 1;2,20 / 0;35,11,
EG / GZ = 2;39,51 / 0;35,11,
y EG * GZ = 1;33,44.
Además GA / AD = 58;50 / 43;10,
DG / GH = 102;0 / 15;40,
y DG * GH = 1598;0.
Dividiendo [1598 por 1;33,44], nos da 1022;54,7, cuya raíz cuadrada es, 31;58,58, multiplicada por la proporción anterior ΘZ / ZG, da, en términos de los tamaños de arriba de GA y AZ [por ej. 58;50 y 43;10],
ΘZ = 33;13,36p,
GZ = 18;45,16p en las mismas unidades,
y, por suma, GΘ = 51;58,52p.
Por consiguiente, donde las hipotenusas AZ y AG son cada una de 120p [respectivamente],
ZΘ = 92;22,3p
y GΘ = 106;1,23p [8].
Los arcos [correspondientes] son:
arco ZΘ = 100;39,34º
y arco GΘ = 124;8,22º.
Por consiguiente el ^ ZAΘ = 50;19,47º
y el ^ GAΘ = 62;4,11º.
Y, por sustracción, el ^ ZGA, que representa la [cantidad del movimiento] retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 27;55,49º, mientras el ^ ZAH, que representa el [movimiento en] anomalía aparente, es de [^ GAΘ - ^ ZAΘ =] 11;44,24º. A esto último le corresponden [movimientos de] 20;53,30º en longitud corregida, y 20;4,30º en longitud media, de acuerdo a las proporciones [de las velocidades] en el perigeo [9]. En consecuencia
| la mitad del [movimiento] retrógrado llega a | [27;55,49º - 20;53,30º =] 7;2,19º y alrededor de 20 ⅓ días. |
| El [movimiento] retrógrado total es de | 14;4,38º y 40 ⅔ días. |
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ No obstante uno calcula, 0;37,32 que podría ser el [valor] más preciso. De la relación (en el comienzo del Libro IX Capítulo 3) 5 revoluciones en anomalía le corresponden 8 revoluciones en longitud menos 2 ¼º, uno encuentra 0;37,31,45..., y el mismo [valor] en el movimiento medio diario derivado a tres lugares [decimales]. Incluso tomando solo dos lugares (0;36,59 / 0;59,8), uno toma 0;37,31,31...
- ↑ Leer seg. (en el manuscrito C²) en cambio de seg. (1057;50,6) en H483,22. Esto último es una enmienda de Heiberg para la lectura de varios manuscritos, seg. (1057;56), que yo tomo seg. como una corrupción en la escritura. Corregido a dos lugares fraccionarios da 1057;51,4, y Ptolomeo no comete un error de cálculo indicado por la cantidad dada por la raíz cuadrada. La lectura en los manuscritos D y Ar (1057;50,56) es también consistente con la raíz cuadrada, aunque parece ser una corrección sobre conjeturas (y sin fundamentos) del valor corrupto de 1057;56.
- ↑ 12;52,24 / 0;37,31 es, precisamente de, 20;35,17.
- ↑ Para un Centrum Verdadero (κ) de 20;35,19 la distancia del centro del Epiciclo es de 61;10,6p (≈ 61;15p - 5'), y para κ = 180º - 20;35,19º la distancia es de 58;49,41p ≈ 58;45p + 5'.
- ↑ Para Venus, el incremento entre los valores sucesivos de la ecuación en la Tabla de la Anomalía es de 14' para 6º del argumento cerca del apogeo, por consiguiente 2 ⅓' para 1º. Sin embargo, uno debería tomar el incremento que es de 15', entre 18º y 24º, llegando a 2 ½' para 1º.
- ↑ Cf. Libro XII Capítulo 2, nota de referencia nro. 16. Cálculo: 14;3,47º * 1 / 0;39,51 ≈ 21º [exactamente 21;10,26º], para lo cual le corresponde una ecuación de 0;50º [exactamente 0;50,30º]. [Cálculo:] 14;3,47º - 0;50º = 13;13,47º ≈ 13;13 ½º. [Luego:] 13;13 ½º * 1 / 0;37,31 = 21;9,3º, y 21;9,3º - 0;50º = 20;19,3º.
- ↑ Esto corresponde a un incremento de 7' para un incremento de 3º en el argumento. Para Venus en la Tabla de la Anomalía, cerca del perigeo, el incremento es de 7' entre los 165º y 162º y entre los 159º y 156º, pero entre los 162º y 159º, que es el intervalo propio (κ ≈ 20º), es de solo 6'.
- ↑ Cálculos [actuales] dan 106;1,26p, y quizás uno debería corregir esto, que [se halla] en la lectura del manuscrito Is. Sin embargo, un arco de 124;8,22° esta en mejor acuerdo con una cuerda de 106;1,23p
- ↑ Cf. Libro XII Capítulo 2, nota de referencia nro. 16. Cálculo: 11;44,24º * 1 / 0;35,11 = 20;1,15º ≈ 20º. Para (180º - 20º) le corresponde una ecuación de 0;49º. [Luego:] 11;44,24º + 0;49º = 12;33,24º ≈ 12;33º. [Después:] 12;33º * 1 / 0;37,31 ≈ 20;4 ½º [precisamente 20;4,16º]. [Finalmente:] 20;4 ½º + 0;49º = 20;53,20º.