Almagesto: Libro XII - Capítulo 04
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración del [Movimiento] Retrógrado de Marte}
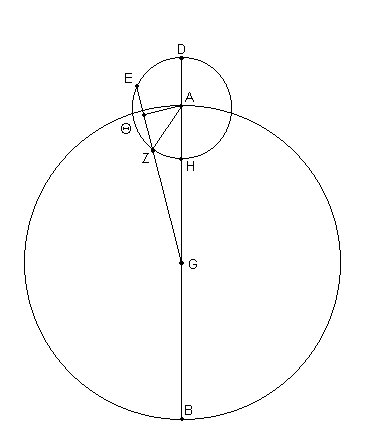
Nuevamente, en el caso de Marte [ver Fig. 12.10], de acuerdo a nuestros cálculos, en la distancia media [más] cercana,
ΘZ / ZG = 1 / 0;52,51 [1],
y EG / GZ = 2;52,51 / 0;52,51,
entonces EG * GZ = 2;32,15.
Además, GA / AH = 60 / 39;30,
y DG / GH = 99;30 / 20;30,
entonces DG * GH = 2039;45.
Dividiendo [2039;45 por 2;32,15], nos da 803;50,50 [2], cuya raíz cuadrada es, 28;21,8, multiplicada por la proporción de arriba de ΘZ / ZG, da, en términos de los tamaños anteriores de GA y AZ [por ej. 60 y 39;30],
ΘZ = 28;21,8p,
GZ = 24;58,25p en las mismas unidades,
y, por suma, GΘ = 53;19,33p.
Por lo tanto, en unidades donde las hipotenusas AZ y AG son cada una de 120p [respectivamente],
ZΘ = 86;8,0p
y GΘ = 106;39,6p.
Los arcos correspondientes son
arco ZΘ = 91;44,34º
y arco GΘ = 125;26,10º.
Por consiguiente el ^ ZAΘ = 45;52,17º
y el ^ GAΘ = 62;43,5º.
Y, por sustracción, el ^ ZGA, que representa el [Movimiento] Retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 27;16,55º, y el ^ ZAH, que representa el [movimiento en] anomalía, es de [^ GAΘ - ^ ZAΘ =] 16;50,48º. A la cantidad reciente le corresponden 19;7,33º en movimiento [medio] longitudinal, de acuerdo a la proporción anterior [de las velocidades, de 1 / 0;52,51]. De este modo
| la mitad del [movimiento] retrógrado es de | [27;16,55º - 19;7,33º =] 8;9,22º y alrededor de 36 ½ días. |
| Y el [movimiento] retrógrado total es de | 16;18,44º y 73 días. |
[Por consiguiente] la distancia en la elongación de las [Posiciones] Estacionarias desde el apogeo y desde el perigeo es [respectivamente] alrededor de 0;20p de la distancia media [por ej. 60p] menor que la máxima distancia, y alrededor de la misma cantidad mayor que la mínima distancia [3].
De acuerdo a nuestros cálculos dado que cerca de la máxima distancia, la ecuación correspondiente a un argumento de 1º para la corrección [de las velocidades] es hallada ser de 10 ⅓' [4]. Por lo tanto
ΘZ / ZG = 0;49,40 / 1;3,11,
EG / GZ = 2;42,31 / 1;3,11,
y EG * GZ = 2;51,8.
Además, GA / AH = 65;40 / 39;30,
DG / GH = 105;10 / 26;10,
y DG * GH = 2571;51,40.
Y, cuando dividimos [2751;51,40 por 2;51,8], nos da 964;48,47, cuya la raíz cuadrada es, 31;3,41, multiplicada por la proporción anterior de ΘZ / ZG, da, en términos de los tamaños de arriba de GA y AZ [por ej. 65;40 y 39;30],
ΘZ = 25;42,43p,
GZ = 32;42,34p,
y, por suma, GΘ = 58;25,17p.
Por consiguiente, expresadas en unidades donde las hipotenusas AZ y AG son cada una de 120p [respectivamente],
ZΘ = 78;6,44p
y GΘ = 106;45,36p.
Los arcos correspondientes son
arco ZΘ = 81;13,8º [5]
y arco GΘ = 125;39,46º.
Por consiguiente el ^ ZAΘ = 40;36,34º
y el ^ GAΘ = 62;49,53º.
Y, por sustracción, el ^ ZGA, que representa el [movimiento] retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 27;10,7º, mientras el ^ ZAH, que representa el [movimiento en] anomalía aparente, es de [^ GAΘ - ^ ZAΘ =] 22;13,19º. A esto último le corresponden [movimientos en] longitud corregidos de 17;13,21º, y en la longitud [media] de 20;58,21º [6], de acuerdo a las proporciones [de las velocidades] en el apogeo. Por consiguiente
| la mitad del [movimiento] retrógrado es de | [27;10,7º - 17;13,21º =] 9;56,46º y alrededor de 40 días, |
| y el [movimiento] retrógrado total es de | 19;53,52º y 80 días. |
De acuerdo a nuestros cálculos dado que cerca de la mínima distancia, la ecuación [correspondiente a un argumento de 1º] para la corrección de [las velocidades], es hallada ser de 12 ⅔' [7]. Por consiguiente
ΘZ / ZG = 1;12,40 / 0;40,11.
EG / GZ = 3;5,31 / 0;40,11,
y EG * GZ = 2;4,14.
Además, GA / AH = 54;20 / 39;30,
DG / GH = 93;50 / 14;50,
y DG * GH = 1391;51,40.
Dividiendo [1391;51,40 por 2;4,14], tomamos 672;13, cuya raíz cuadrada es, 25;55,38, multiplicada por la proporción de arriba de ΘZ / ZG, da, en términos de los tamaños de arriba GA y AZ [por ej. 54;20 y 39;30],
ΘZ = 31;24,3p,
GZ = 17;21,51p en las mismas unidades,
y, por adición, GΘ = 48;45,54p.
Por consiguiente, donde las hipotenusas AZ y AG son cada una de 120p [respectivamente],
ZΘ = 95;23,42p
y GΘ = 107;42,7p.
Los arcos correspondientes son
arco ZΘ = 105;18,10º
y arco GΘ = 127;40,22º [8].
Por consiguiente el ^ ZAΘ = 52;39,5º
y ^ GAΘ = 63;50,11º.
Y, por sustracción, el ^ ZGA, que representa la [cantidad del movimiento] retrógrado debido a la velocidad del planeta, es de [90º - ^ GAΘ =] 26;9,49º, mientras el ^ ZAH, que representa el [movimiento en] anomalía aparente, es de [^ GAΘ - ^ ZAΘ =] 11;11,6º. A este último le corresponden [movimientos en] longitud corregida de 20;33,42º, y en longitud media de 16;52,52º, de acuerdo a las proporciones [de las velocidades] en el perigeo [9]. Entonces
| la mitad del [movimiento] retrógrado llega a ser como de | [26;9,49º - 20;33,42º =] 5;36,7º y alrededor de 32 ¼ días, |
| y el [movimiento] retrógrado total es de | 11;12,14º y 64 ½ días. |
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ De los movimientos medios diarios (Libro IX Capítulo 4): 0;27,41,40 / 0;31,26,36 = 0;52,50,47...
- ↑ El [valor] exacto podría ser 803;50,33, que es hallado como la lectura de segunda mano (revisión) en el manuscrito D. El manuscrito de Ger (Gerardo de Cremona) tiene 803;50,32, el manuscrito T 803;50,30. La variación no tiene futuras consecuencias, dado que la raíz cuadrada de todo es de 28;21,8 (al segundo más cercano).
- ↑ Para un Centrum Verdadero (κ) de 19;7,33º, la distancia del centro del Epiciclo es de, ρ = 65;38,12p ≈ 66p - 22'. Para κ = 160;52,27º, ρ = 54;17,56p ≈ 54p + 18', por ej. 20' es un [valor] medio razonable.
- ↑ Para Marte, en la Tabla de la Anomalía, un argumento de 18º le corresponde una ecuación de 3;13º y para 24º, 4;16º; por lo tanto, como Manitius señala, la cantidad correcta correspondiente a 1º debería ser (4;16 - 3;13) / 6 = 10 ½'.
- ↑ El correcto podría ser 81;13,28º, y esta es la lectura en los manuscritos B, C, L y en el de Ger (Gerardo de Cremona). Sin embargo, todos los manuscritos están de acuerdo con la lectura de la mitad de estos 40;36,34º, que parecerían confirmar aquí la lectura de Heiberg. Es posible, no obstante, que Ptolomeo cometió un error en la división, y que la lectura '8' en los manuscritos A y D es debido a una corrección del escriba.
- ↑ Ptolomeo da un cálculo para esto en Libro XII Capítulo 6 Fig. R.
- ↑ Para Marte, en la Tabla de la Anomalía, un argumento de 162º le corresponde una ecuación de 3;55º, y para 159º, 4;33º. Por lo tanto para 1º, alrededor de 20º desde el perigeo, le corresponden (4;33 - 3;55) / 3 = 12 ⅔'.
- ↑ Precisamente, 127;40,3º.
- ↑ Cf. Libro XII Capítulo 2 nota de referencia nro. 16. Cálculo: 11;11,6° * 1 / 0;40,11 = 16;42,3º, que le corresponde una ecuación de 3;40,50º [exactamente 3;38,59º: pareciera como que Ptolomeo tomó la ecuación de (180º - 16;51º)]. [Luego:] 11;11,6 + 3;40,50º = 14;51,56º, que multiplicado por 1 / 0;52,51 da 16;52,52º [exactamente 16;52,36º]. [Finalmente:] 16;52,52º + 3;40,50º = 20;33,42º.