Almagesto: Libro XII - Capítulo 09
Nuevamente, sea [Fig. 12.16] la distancia en longitud media de 3° desde el apogeo: en consecuencia la posición media del Sol estará en ♎︎ 13º, y la posición verdadera del Sol en ♎︎ 11;4º. Dibujar BE y en el centro E describir el epiciclo ZH. Como antes, dibujar la tangente GH, y unir EG, EH. Entonces en la ubicación en cuestión, por ej. con el ^ ABE tomado como de 3º, por medio de nuestros métodos anteriores uno puede demostrar que el ángulo corregido para la excentricidad [6] [es],
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de las Máximas Elongaciones de Venus y de Mercurio desde el Sol}
Ahora que hemos pasado a través de los teoremas concernientes a los [Movimientos] Retrógrados, lo siguiente en la secuencia lógica es demostrar las Máximas Elongaciones de los planetas Venus y Mercurio desde el Sol, en cada uno de los signos del Zodíaco, tal como se derivan de las hipótesis anteriores. Estableciendo [las tablas] para ellos, hemos tomado [las elongaciones] con respecto a la posición aparente del Sol, y asumimos que los presentes planetas están al comienzo de los [respectivos] signos, y que las posiciones de sus apogeos con respecto a los puntos Solsticiales y Equinocciales son aquellos que se obtienen en nuestro tiempo, a saber, para Venus, en ♉︎ 25º, y, para Mercurio en ♎︎ 10º. Será fácil para [todos] aquellos, que vienen después de nosotros, corregir el cambio en las máximas distancias debido al cambio en los apogeos, utilizando los mismos métodos, y en cualquier caso el cambio permanece inalterable por un muy largo tiempo.
Con el fin de que sea fácil de entender el método de nuestras aproximaciones [a este problema], por el camino del ejemplo, debemos demostrar primero para Venus, las máximas elongaciones de la mañana y de la tarde (definida anteriormente) cuando el planeta esta en el equinoccio de primavera, [a saber] en el comienzo de Aries.
Sea ABGDE [Fig. 12.13] la línea a través de A, el apogeo de la Excéntrica, sobre la cual B es tomado como centro del movimiento uniforme, G como el centro de la excéntrica transportando el Epiciclo, y D como el centro de la eclíptica. Dibujar GZ como radio de la excéntrica, describir el epiciclo HΘ alrededor de Z, y desde D dibujar DΘ como tangente sobre el lado del epiciclo que representa [la visibilidad del planeta] por la mañana y esta hacia adelante de [su centro]. Unir BZH y ZΘ, y eliminar las perpendiculares GK, GL y BM.
Entonces, dado que DA apunta hacia ♉︎ 25º y DΘ hacia el comienzo de Aries,
el ^ ADΘ = 55º donde 4 ángulos rectos = 360º
el ^ ADΘ = 110º donde 2 ángulos rectos = 360ºº;
y el ^ DGK = 70ºº (complementario).

Por lo tanto, en el círculo alrededor del triángulo rectángulo GDK,
arco GK = 110º
y GK = 98;18p donde la hipotenusa GD = 120p.
Por lo tanto donde GD = 1;15p y el radio del epiciclo, ZΘ = 43;10p
GK = (= LΘ) = 1;1p,
y, por sustracción [de LΘ desde ZΘ], ZL = 42;9p,
donde GZ, el radio de la excéntrica, esta tomada como 60p.
Por lo tanto donde la hipotenusa GZ = 120p, ZL = 84;18p,
y, en el círculo alrededor del triángulo rectángulo GZL,
arco ZL = 89;16º.
En consecuencia el ^ ZGL = 89;16ºº donde 2 ángulos rectos = 360ºº.
Pero el ^ DGK = 70ºº en las mismas unidades, y el ^ LGK es recto.
En consecuencia, por suma, el ^ ZGD es encontrado ser de [89;16 + 70 + 180] = 339;16ºº,
y, por sustracción [desde 2 ángulos rectos], el ^ AGZ = 20;44ºº.
Por lo tanto, en el círculo alrededor del triángulo BGM,
arco BM = 20;44º
y arco GM = 159;16º (suplementario).
Por lo tanto las cuerdas correspondientes
BM = 21;35p donde la hipotenusa BG = 120p
y GM = 118;2p donde la hipotenusa BG = 120p.
Por lo tanto donde BG = 1;15p, y GZ, el radio de la excéntrica, es de 60p,
BM = 0;13p,
GM = 1;14p,
y, por sustracción [de GM desde GZ], MZ = 58;46p.
Por lo tanto la hipotenusa BZ [= (BM² + MZ²) ^ 0,5] = 58;46p en las mismas unidades.
Por consiguiente, donde BZ = 120p, BM = 0;27p,
y, en el círculo alrededor del triángulo rectángulo BZM,
arco BM = 0;26º.
En consecuencia el ^ BZG = 0;26ºº donde 2 ángulos rectos = 360ºº.
Y demostramos que el ^ AGZ = 20;44ºº en las mismas unidades.
Por lo tanto, por suma, el ^ ABZ, que representa el movimiento medio en longitud,
es 21;10ºº donde 2 ángulos rectos = 360ºº
es 10;35º donde 4 ángulos rectos = 360º.
En consecuencia la posición media del Sol será de 10;35º hacia adelante del apogeo en A, y, obviamente, estará en ♉︎ 14;25º.
Y la posición verdadera del Sol estará en ♉︎ 15;14º.
Por lo tanto, cuando el planeta esta al comienzo de Aries, por la mañana tendrá una máxima elongación de 45;14º desde el Sol verdadero.

Nuevamente, a continuación sea dibujado el diagrama [Fig. 12.14] con la tangente a un lado del epiciclo que representa [la visibilidad] de la tarde y esta hacia atrás del [centro del] epiciclo, mientras el planeta, como antes, se toma estando al comienzo de Aries.
Por lo que se demuestra arriba, el ^ ADΘ seguirá siendo el mismo,
y el ^ DGK = 70ºº donde 2 ángulos rectos = 360ºº,
y GK = LΘ = 1;1p
Donde GZ, el radio de la excéntrica, es de 60p,
y ZΘ, el radio del epiciclo, es de 43;10p.
Por lo tanto, por suma, ZL [= ZΘ + LΘ] = 44;11p en las mismas unidades.
Y es obvio que, donde la hipotenusa [del triángulo GZL] GZ = 120p,
ZL = 88;22p,
y, en el círculo alrededor del triángulo rectángulo GZL,
arco ZL = 94;51º.
En consecuencia el ^ ZGL = 94;51ºº donde 2 ángulos rectos = 360ºº,
y ^ ZGK = 85;9ºº (complementario).
Entonces, por suma, el ^ ZGD (= ^ BGM) [= ^ DGK + ^ ZGK] = 155;9ºº en las mismas unidades.
Por consiguiente, en el círculo alrededor del triángulo rectángulo BGM,
arco BM = 155;9º
y arco GM = 24;51º (suplementario).
Por lo tanto las cuerdas correspondientes
BM = 117;11p donde la hipotenusa BG = 120p
y GM = 25;49p donde la hipotenusa BG = 120p.
Por lo tanto, donde BG = 1;15p,
BM = 1;13p,
MG = 0;16p,
y, por suma, MZ = 60;16p.
Por lo tanto la hipotenusa BZ [= (BM² + MZ²) ^ 0,5] = 60;17p en las mismas unidades.
Por lo tanto, donde BZ = 120p, BM = 2;25p,
Y, en el círculo alrededor del triángulo rectángulo BZM,
arco BM = 2;19º.
En consecuencia el ^ BZM = 2;19ºº donde 2 ángulos rectos = 360ºº.
Y el ^ BGZ = 204;51ºº en las mismas unidades,
dado que el ^ DGZ fue demostrado ser de 155;9ºº en esas unidades.
Por lo tanto, por adición, el ^ ABZ, que representa el movimiento medio en longitud [2],
viene a ser de 207;10ºº donde 2 ángulos rectos = 360ºº
viene a ser de 103;35º donde 4 ángulos rectos = 360º.
Por lo tanto la posición media del Sol estará en (♉︎ 25º - 103;35º =) ♒︎ 11;25º y su posición verdadera en ♒︎ 13;38º.
En consecuencia, por la tarde la máxima elongación del planeta será de 46;22º desde el Sol verdadero, cuando, como antes, [el planeta] esta al comienzo de Aries.
En el caso del planeta Mercurio, con el fin de tener un enfoque más práctico para las demostraciones que faltan de sus fases, las cuáles daremos más adelante [3], establezcamos nosotros mismos la tarea de encontrar la máxima elongación del planeta desde la posición verdadera del Sol, como estrella de la tarde cuando [Mercurio] esta al comienzo de Scorpius, y como estrella de la mañana cuando esta al comienzo de Taurus.
Ahora, de acuerdo con nuestras hipótesis para Mercurio, cuando la posición aparente del planeta esta dada, la posición media en longitud no puede ser hallada, dado que la línea GZ no conserva la misma longitud constante [4], siempre igual al radio de la excéntrica (como esta lo hace en la hipótesis de los otros [planetas]). Pero si la posición media en longitud esta dada, la posición aparente puede ser demostrada. Entonces asumimos, para cada signo [zodiacal], dos posiciones en longitud [media] las cuales puede llevar al planeta [a la máxima elongación] cerca del comienzo del signo en cuestión, la primera hacia adelante [del comienzo del signo], y la segunda hacia atrás [de él]; calculamos las máximas elongaciones en las posiciones elegidas, y desde allí [5] encontramos la máxima elongación que ocurre en el actual comienzo del signo. Esto será fácilmente comprensible a partir de los problemas [en particular] que hemos establecido nosotros mismos para resolver: y primero para la máxima elongación de la tarde al comienzo de Scorpius.
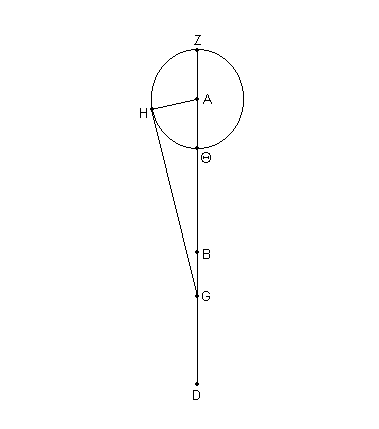
Sea ABGD [Fig. 12.15] el diámetro a través del apogeo A, sobre el que G es tomado como centro del epiciclo, y B como el centro del movimiento uniforme del epiciclo. Primero sea el centro del epiciclo imaginado precisamente como en el apogeo, entonces la posición media en longitud del Sol estará en ♎︎ 10º, y su longitud verdadera en ♎︎ 8º. Sobre el centro A describir el epiciclo ZH, dibujar GH como tangente al lado de él representando la tarde, y eliminar la perpendicular AH.
Entonces, dado que en nuestro tratamiento previo (Libro IX Capítulo 9, Fig. 9.8) donde se demostró que GA, la máxima distancia, es [igual a] 69p, [y] AH, el radio del epiciclo, es de 22 ½p,
donde la hipotenusa [del triángulo rectángulo AGH] AG = 120p,
AH = 39;8p,
y, en el círculo alrededor del triángulo rectángulo AGH,
arco AH = 38;4º,
y el ^ AGH = 38;4ºº donde 2 ángulos rectos = 360ºº
y el ^ AGH = 19;2º donde 4 ángulos rectos = 360º.
Y GA esta en ♎︎ 10º.
Por lo tanto el planeta tendrá una posición de ♎︎ 29;2º, [y] su máxima elongación desde la posición verdadera del Sol siendo de 21;2º.
el ^ AGE = 2;52º,
y la distancia del epiciclo en esta ubicación [7],
EG ≈ 68;58p donde EH, el radio del epiciclo, es de 22;30p.
Por lo tanto, donde la hipotenusa EG = 120p, EH = 39;9p.

Por lo tanto, en el círculo alrededor del triángulo rectángulo GEH,
arco EH = 38;5º,
y el ^ EGH = 38;5ºº donde 2 ángulos rectos = 360ºº
y el ^ EGH = 19;3º, aproximadamente, donde 4 ángulos rectos = 360º.
Por consiguiente, por suma, el ^ AGH = 21;55º en las mismas unidades.
Entonces cuando el planeta esta en ♏︎ 1;55º, su máxima elongación desde la posición verdadera del Sol será de (♏︎ 1;55º - ♎︎ 11;4º =) 20;51º.
Y demostramos que cuando [el planeta] esta en ♎︎ 29;2º, su máxima elongación desde la posición verdadera del Sol será de 21;2º.
Así la diferencia entre las longitudes es de 2;53º, y la diferencia entre las máximas elongaciones es 11', y entonces para los 0;58º desde la primera posición hasta el comienzo de Scorpius corresponde [una disminución en la máxima elongación por] alrededor de 4', los cuáles restamos de los 21;2º para obtener la máxima elongación por la tarde de 20;58º desde la posición verdadera del Sol, [cuando el planeta esta] precisamente al comienzo de Scorpius.
Seguidamente, para encontrar la máxima elongación de la mañana al comienzo de Taurus, supongamos primero que la posición media en longitud es de 39º hacia atrás desde el perigeo. Por lo tanto la posición media del Sol esta en ♉︎ 19º, y el Sol verdadero en ♉︎ 19;38º. Sea allí dibujada una figura [Fig. 12.17] similar [a la precedente], en la que el epiciclo esta descrito hacia atrás del perigeo, y la tangente es dibujada hacia el lado de la mañana del epiciclo.

Entonces en la posición en cuestión, por ej. con el ^ DBZ tomado como de 39º, uno puede demostrar por el método anteriormente descrito que
el ^ DGE = 40;57º [8],
Y que la distancia en ese momento,
GE = 55;59p donde el radio del epiciclo, EH = 22;30p.
Por lo tanto donde la hipotenusa [del triángulo rectángulo GEH] GE = 120p,
EH = 48;14p
y, el círculo alrededor del triángulo rectángulo GEH,
arco EH = 47;24º.
En consecuencia el ^ EGH = 47;24ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ EGH = 23;42º donde 4 ángulos rectos = 360º.
Y, por sustracción [desde el ^ DGE], el ^ HGD = 17;15º en las mismas unidades.
Por lo tanto cuando el planeta Mercurio tiene una longitud de ♈︎ 27;15º, su máxima elongación por la mañana desde la posición verdadera del Sol sería de (♉︎ 19;38º - ♈︎ 27;15º =) 22;23º.
Nuevamente, suponer que se tiene una distancia en longitud media de 42º desde el perigeo, sobre el mismo lado. Así el Sol tendrá una longitud media de ♉︎ 22º y una longitud verdadera de ♉︎ 22;31º.
Entonces en esta posición, por ej. con el ^ DBZ tomado como de 42º, uno puede demostrar que
el ^ DGE = 44;4º,
y que la distancia en este momento,
GE = 55;53p [9] donde el radio del epiciclo, EH = 22;30p.
Por lo tanto, donde la hipotenusa EG = 120p, EH = 48;19p,
y, en el círculo alrededor del triángulo rectángulo EGH,
arco EH = 47;30º.
En consecuencia el ^ EGH = 47;30ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ EGH = 23;45º donde 4 ángulos rectos = 360º,
y, por sustracción [desde el ^ DGE], el ^ HGD = 20;19º en las mismas unidades.
Por lo tanto cuando el planeta Mercurio tiene una longitud de ♉︎ 0;19º [10], su máxima elongación de la mañana desde la posición verdadera del Sol sería de (♉︎ 22;31º - ♉︎ 0;19º =) 22;12º. Y demostramos que cuando [el planeta] tiene una longitud de ♈︎ 27;15º, su máxima elongación (definida similarmente) será de 22;23º.
Entonces, nuevamente, dado que la diferencia entre las longitudes es de 3;4º, y la diferencia entre las máximas elongaciones es de 11', para los 2;45º desde la longitud en la primera posición hasta el comienzo de Taurus, le corresponde aproximadamente 10'. Por ende, restando lo último desde los 22;23º, obtenemos la máxima elongación por la mañana de 22;13º desde la posición verdadera del Sol [cuando el planeta esta] al comienzo de Taurus.
Lo que se ha requerido para examinar.
Por el mismo camino calculamos las máximas elongaciones de la mañana y de la tarde para ambos planetas por [medio del] cálculo [al comienzo de] los otros signos, y construimos una pequeña tabla para ellos, con 12 líneas (iguales en número [para los signos]) y con 5 columnas. Al comienzo colocamos, en la primera columna, los primeros puntos de los signos, comenzando con Aries. En las siguientes 4 columnas ponemos las máximas elongaciones correspondientes calculadas desde la posición verdadera del Sol: la segunda contiene las elongaciones por la mañana del planeta Venus, la tercera su elongación por la tarde, la cuarta las elongaciones por la mañana de Mercurio, y la quinta sus elongaciones por la tarde. La tabla es la siguiente.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro XII |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Ver HAMA 230-4, Pedersen 351-4.
- ↑ Leer (en los manuscritos D¹, G y Ar) en H513,15-16 para el absurdo . Corregido por Manitius.
- ↑ La referencia es a Libro XIII Capítulo 8, Fig. 13.23.
- ↑ Para los otros planetas (por ej. para Venus, Fig. 12.14) se denota la distancia desde el centro de la excéntrica hasta el centro del epiciclo, pero para Mercurio Ptolomeo parece referirse a una figura tal como la Fig. 9.9, donde esta denota la distancia desde el punto de la Ecuante al centro del epiciclo. Incluso esas dos cantidades son trigonométricamente comparables. Ptolomeo esta en lo correcto en establecer que, para Mercurio, uno no puede encontrar la posición media desde la verdadera, al menos por la Geometría Euclidiana.
- ↑ Por interpolación lineal.
Método de Interpolación por Lagrange. Click en la imagen para ampliar
Fórmula de interpolación solamente entre 2 pares de valores o puntos (X;Y), (i = 0 y 1 en Fórmula Polinómica de Lagrange).
α es el argumento a "entrar" en la columna de las X y el "Valor Interpolado" resulta de la columna de las Y.
Para una interpolación con más de 2 pares de valores (X;Y) verː Método de Interpolación por Lagrange, aunque para los valores que interpola Ptolomeo, con esta fórmula sencilla y reemplazándola con los 4 valores de una tabla, da el mismo resultado que el del astrónomo.
Nota del traductor al español. - ↑ Si aquí el texto es confiable, debe ser el significado de . Pero la referencia normal de tal expresión podría ser por sí misma para la Ecuación (del centro), no para el ángulo corregido por la ecuación. Tengo la firme sospecha que la frase esta interpolada (esta en toda la tradición del manuscrito).
- ↑ Por cálculos trigonométricos, EG = 68;58,25p, el ^ AGE = 2;52,10º.
- ↑ Para seg. κ = 219º, ρ = 55;59,1p, y κ = 220;55,57º, por consiguiente el ^ DGE ≈ 40;56º.
- ↑ Leer seg. seg. en H519,13 cambiando por seg. seg. ν (55;50p). Cálculos (para seg. κ = 222º) da ρ = 55;52,58p. Aunque Ptolomeo es capaz de [cometer] un error de cálculo por esta cantidad, de hecho no lo hizo, dado que para los siguientes cálculos son consistentes con 55;53p y no con 55;50p (en consecuencia 22;30 * 120 / 55;50 = 48;21 ½), mientras [que los] 55;53 [los] deriva a 48;19, como [se lee en] el texto). El error, a pesar de escritura, es [muy] antiguo, dado que es compartido en todos los manuscritos.
- ↑ Literalmente "de 19' del primer grado de Taurus".