Almagesto: Libro V - Capítulo 12
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre la construcción de un Instrumento Paraláctico}
Contrariamente, para que evitemos adquirir factores inciertos en nuestro examen sobre este tema, construimos un instrumento que nos permita observar tan precisamente como sea posible, la cantidad de la Paralaje Lunar, y su Distancia Cenital, a lo largo del gran círculo a través de los polos del Horizonte y de la Luna.
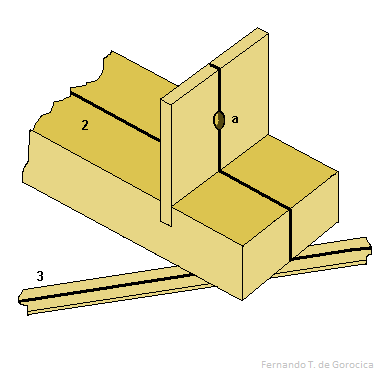
Fabricamos dos listones [Fig. G,1,2], rectangulares [en su sección transversal], no menor que 4 Codos de largo, tal que admitan una graduación más precisa, y con una sección transversal de tamaño suficiente [de modo] que no fuesen doblados debido a su longitud, sino que cada lado conformados estrictamente en una línea recta. Luego dibujamos una línea recta a lo largo del medio del lado más ancho de cada listón, y fijamos en uno de ellos [Fig. G,2], en cada extremo, centrado sobre la línea, y perpendicular [a él], dos planchuelas rectangulares, de igual tamaño y paralelas una con la otra [Fig. G,a,b]; cada planchuela tiene un agujero [circular] exactamente en el centro, siendo el orificio [inferior] el más pequeño para el ojo, y aquel [que apunta] hacia la Luna el mayor [(el superior)], de tal manera que cuando un ojo se coloque en la planchuela de menor apertura, toda la Luna pudiese ser visible a través de la apertura en la otra planchuela, la cual fue alineada [con el primer orificio de la planchuela inferior]. Hacemos una perforación de igual tamaño a través de ambos listones al final [parte superior] de la línea media cerca de la planchuela con el orificio mayor, y fijamos una clavija [Fig. G,c] a través de ambas perforaciones de tal modo que los lados de los listones inscriptos con sus líneas [2] fuesen ajustados conjuntamente alrededor de la clavija como centro, aunque el listón con las planchuelas pueda girar libremente en todas las direcciones sin doblarse [(moverse)]. Calzamos el listón sin las planchuelas [el vertical: Fig. G,1] dentro de una base [Fig. G,4]. Sobre la línea media de cada listón, al final por la base, tomamos un punto tan lejos como fuera posible desde el centro de la clavija (la misma distancia desde ella [en ambos listones]), y, sobre el listón con la base, dividimos la línea marcándola dentro de 60 secciones, subdividiendo cada sección dentro de tantas divisiones como fuera posible. También fijamos en la parte trasera del mismo listón [fijo], en los extremos, [dos] planchuelas [Fig. G,d,d] teniendo sus caras correspondientes alineadas [(paralelas)] una con la otra [3], y cada una equidistante en todos los aspectos de esa misma línea media, entonces cuando una línea a plomo [(Plomada)] es suspendida entre ellas, el listón [fijo] puede estar emplazado exactamente perpendicular al plano del horizonte.
También ya tenemos la línea (Meridiana) [Fig. G,e] dibujada en el plano paralelo aquel del horizonte en un lugar sin sombra. Colocamos el instrumento en posición vertical de tal manera que los lados de los listones estuviesen mantenidos al ras uno con el otro por [medio de] la clavija ubicándose en el meridiano, siendo paralelo a la línea meridiana, y el listón con su base fijado exactamente [en forma] perpendicular, en una posición firme e inamovible, mientras el otro listón pueda moverse en el plano del meridiano [girando] alrededor de la clavija, respondiendo al empuje [del usuario] [4].
También agregamos otro listón, recto y delgado, [Fig. G,3] fijado por una pequeña clavija [Fig. G,f] en la base al final de la línea graduada, donde también pueda ser girado, y lo suficientemente largo para alcanzar el fin de la línea sobre el otro listón equidistante [desde la clavija] cuando este [último] girase hasta su máxima distancia [desde la base] [5]; por lo tanto girándolo en el mismo instante como el último, uno pueda utilizarlo para mostrar la distancia sobre la línea recta [que une] los extremos [de las líneas centrales de los dos listones].

Realizamos nuestras observaciones de la Luna del siguiente modo. La Luna ha sido localizada en el meridiano [del lugar], y cerca de [alguno de] los Solsticios sobre la Eclíptica, dado que en tales situaciones el gran círculo a través de los polos del horizonte y el centro de la Luna coincide próximamente con el gran círculo a través de los polos de la eclíptica, a lo largo del cual es tomada la latitud de la Luna. Además la distancia verdadera [de la Luna] desde el Cenit también puede ser determinada convenientemente desde la misma ubicación [observación]. Cuando la Luna se ubica precisamente en el meridiano, movimos el listón con las planchuelas [de observación] "alrededor" [(desde arriba hacia abajo y viceversa)] hasta una posición en la que el centro de la Luna, cuando es observado a través de ambos orificios, se situó en el centro del orificio más grande. Marcamos sobre el listón más delgado la distancia entre los extremos de las líneas sobre los [dos] listones, [(distancia medida sobre tal listón delgado desde su extremo inferior, desde la clavija que coincide con la línea graduada del listón vertical fijo, hasta la coincidencia con la otra línea sobre el listón giratorio)], luego aplicamos la distancia [marcada sobre el listón más delgado] hasta la línea graduada dentro de 60 secciones del listón en posición vertical. Por lo tanto encontramos la cantidad de esa distancia en aquellas unidades en las que el radio del círculo descrito por la rotación [del listón con las planchuelas de observación] en el plano del meridiano, contiene 60 [(de estas unidades)]. Calculando el arco correspondiente a aquella cuerda, encontramos la distancia angular del centro aparente de la Luna desde el cenit, medido a lo largo del gran círculo a través de los polos del horizonte y del centro de la Luna, que coincide en aquel instante con el [gran círculo] a través de los polos del Ecuador y de la Eclíptica, [por ej. con] el meridiano.
Primero, con el fin de determinar la cantidad precisa de la Máxima Desviación Lunar en Latitud, hicimos unas observaciones cuando la Luna se ubicó simultáneamente cerca del solsticio de verano y cerca del límite Norte de su círculo inclinado [6]. Dado que en la región de aquellos puntos la latitud de la Luna se mantiene sensiblemente igual durante un intervalo considerable, y además, dado que entonces la Luna esta muy cerca del Cenit en el paralelo a través de Alejandría (ciudad en la que hicimos las observaciones), su posición aparente es aproximadamente la misma como su posición verdadera. En tales situaciones se encontró que la distancia desde el centro de la Luna desde el cenit fue siempre hallada alrededor de los 2 ⅛º. Por lo tanto también por este método la mayor latitud de la Luna a ambos lados de la eclíptica es demostrada ser de 5º. La distancia cenital desde el Ecuador en Alejandría ha sido demostrada ser de 30;58º [(siendo la latitud Norte terrestre)]; si sustraemos desde esta los 2 ⅛º (que es la distancia aparente [del centro de la Luna desde el cenit]), el resultado [28;50 ½º] es alrededor de 5º mayor que la distancia desde el Ecuador hasta el solsticio de verano que fue demostrada ser de 23;51º [(Oblicuidad de la Eclíptica)].
Entonces, con el fin de atacar el problema de las paralajes, observamos la Luna del mismo modo, pero en un instante cuando esta estuvo cerca del solsticio de invierno, ambas [situaciones] por la razón [arriba] ya mencionada y porque su distancia desde el cenit en aquella ubicación es la mayor de todas esas posiciones meridianas, y por consiguiente nos brindan una mayor y más fácil determinación de la paralaje. Plantearemos una de un número de observaciones de las paralajes que hicimos en tales situaciones [de la Luna]. Por este medio vamos a demostrar el método de cálculo y al mismo tiempo proveer una demostración del resto de lo que sigue en el orden apropiado.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro V |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 |
Notas de referencia
- ↑ Sobre el instrumento descrito en este capítulo (conocido en la edad media como un "Triquetrum") ver Price, "Instrumentos de Precisión" 589-90 con la Fig. 344. Mi Fig. G esta basada sobre el texto del Almagesto más que sobre la figura dada por Papo de Alejandría en su comentario (Rome [1] I p. 71, con una moderna reconstrucción; ver también las notas de Rome en pp. 70-5).
- ↑ Las caras inscritas de los listones 1 y 2 no pueden estar al ras (coincidentes) una con la otra, como es claro desde la Fig. G. Ptolomeo parece dar a entender que uno solamente ve las caras inscriptas de los dos listones como el radio de un círculo con centro en la clavija c.
- ↑ Eliminando las palabras en H404,17-18. Esto podría significar "cada una teniendo aquella cara que se encuentra en el mismo lado de la línea [graduada] alineada con la otra". Pero es imposible, dado que las planchuelas no se encuentran en el lado de la cara con las graduaciones, sino "en la [cara] de atrás", por ej. sobre la cara opuesta de la línea graduada. Esto también esta claro en la descripción detallada de Papo de Alejandría (Rome p. 75). es un comentario estúpido sobre , que he traducido "correspondiente", aunque significa literalmente "en la misma dirección". La interpolación es antigua, dado que esta es encontrada en la tradición Árabe.
- ↑ Por ej. la clavija mantiene los listones suficientemente juntos y apretados tal que el listón 2 no puede moverse bajo su propio peso, sino lo suficientemente suelto como para que pueda ser girado por el usuario.
- ↑ Este listón de hecho tiene que ser "delgado", ya que tiene que pasar entre los dos listones 1 y 2, y las caras de los mismos están supuestamente al ras (parejas). Papo de Alejandría supera esta dificultad diciendo que el listón 2 tiene que estar ahuecado a lo largo de su longitud hasta la profundidad del grosor del listón 3 (Rome p. 73). Hay una futura dificultad que concuerda con las instrucciones de Ptolomeo de que el listón 3 tiene que ser lo suficientemente largo para alcanzar el final del listón 2 en su máxima rotación, posiblemente hasta los 90º: por lo tanto su longitud debería ser igual a (la √2 * la longitud de la línea graduada). Pero dado que uno mide la cuerda de la distancia cenital, no directamente sobre el listón 3, sino marcándolo sobre el listón 3 y luego midiéndolo en la escala sobre el listón 1, la distancia cenital que puede ser medida no es mayor que 60º (cuya cuerda es de 60p). Por lo tanto, probablemente, Papo (p. 73) dice que el listón 3 debería ser menor que la longitud de la línea graduada. Rome (p. 73 n.0) sugiere que Ptolomeo cambia deliberadamente este límite para evitar las complicaciones de la refracción cercana al horizonte. Parece más probable que, simplemente, sea una parte construida por Ptolomeo, y que el acortamiento del listón de Papo fue hecho para evitar las dificultades que podrían resultar de tratar de aplicar el listón 3 a la línea graduada si esta fuera de 60p o más.
- ↑ Dado que la revolución del nodo [lunar] toma lugar cada 18 ⅔ años, esta ubicación ocurre 9 ⅓ años más temprano o más tarde que de una ubicación similar de la Luna cerca del solsticio de invierno, observada por Ptolomeo (Libro V Capítulo 13) en Octubre del año 135 (d. C.). Por lo tanto estas observaciones fueron hechas tanto en el verano del año 126 (d. C.), como en la primavera del año 145 (d. C.). Esta es la única conclusión útil que puede ser esbozada desde el confuso argumento de Newton, 184-6.