Almagesto: Libro X - Capítulo 07
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Demostración de la Excentricidad y [la posición del] Apogeo de Marte}
En el caso de la Luna tomamos las posiciones y las horas de tres eclipses lunares, y demostramos geométricamente la proporción de la anomalía y la posición del apogeo. Entonces, aquí también, del mismo modo, para cada uno de estos [3] planetas [exteriores], observamos las posiciones de tres Oposiciones para [la posición] media del Sol, tan precisamente [como] sea posible, utilizando los instrumentos Astrolabios, calculados, también, la hora y la posición de los 180º de Elongación [2] a partir de la posición media del Sol en [cada una] de las observaciones, y por consiguiente demostrar la razón de la excentricidad y [la posición del] apogeo.
Entonces, primero para Marte, tomamos las tres oposiciones que observamos del siguiente modo [3].
[1] La primera en el decimoquinto año de Adriano, 26/27 de Tybi [V] en el calendario Egipcio [14/15 de Diciembre de 130], 1 hora equinoccial después de la medianoche, [Marte se encontraba] alrededor de ♊︎ 21º [4].
[2] La segunda en el decimonoveno año de Adriano, 6/7 de Pharmouthi [VIII] en el calendario Egipcio [21/22 de Febrero de 135], 3 horas antes de la medianoche, [Marte se encontraba] alrededor de ♌︎ 28;50º [5].
[3] La tercera en el segundo año de Antonino Pío, 12/13 de Epiphi [XI] en el calendario Egipcio [27/28 de Mayo de 139], 2 horas equinocciales antes la medianoche, [Marte se encontraba] alrededor de ♐︎ 2;34º [6].
Los intervalos entre lo anteriormente [descrito] son los siguientes:
| Desde la oposición [1] hasta la [2] [hay] | 4 años Egipcios 69 días y 20 horas equinocciales |
| Desde la [2] hasta la [3] [hay] | 4 años Egipcios 96 días y 1 hora equinoccial |
Para el primer intervalo, calculamos un movimiento [medio] en longitud de 81;44º, mas allá de revoluciones completas,
y para el segundo intervalo, 95;28º.
Incluso si utilizamos los habituales períodos [(no precisos)] de una vuelta, que listamos anteriormente para calcular los movimientos medios, no habría ninguna diferencia significativa en un intervalo tan corto [7].
Es obvio que el movimiento aparente del planeta, mas allá de revoluciones completas, es de
| para el primer intervalo | 67;50º |
| y para el segundo intervalo | 93;44º |
Luego [ver la Fig. 10.7], sean dibujados allí, en el plano de la Eclíptica, tres círculos iguales: sea ABG el círculo transportando el centro del Epiciclo de Marte con centro en D, EZH la Excéntrica de movimiento uniforme con centro en Θ, y KLM el círculo concéntrico con la Eclíptica con centro en N, y XOPR sea el diámetro a través de los [tres] centros. Sea A el punto en el cual el centro del epiciclo estuvo en la primera oposición, B el punto donde este estuvo en la segunda oposición, y G el punto donde estuvo en la tercera oposición. Unir ΘAE, ΘBZ, ΘHG, NKA, NLB y NGM. Entonces el arco EZ de la excéntrica (Ecuante) es de 81;44º, [siendo] la cantidad del movimiento medio del primer intervalo, y el arco ZH es 95,28º, la cantidad del segundo intervalo.
Además el arco KL de la Eclíptica es de 67;50º, [que es] la cantidad del primer intervalo del movimiento aparente, mientras el arco LM es de 93;44º, [siendo también] la cantidad del segundo intervalo.
Ahora si los arcos EZ y ZH de la excéntrica [ecuante] estuvieron subtendidos por los arcos KL y LM de la eclíptica, esto sería todo lo que necesitaríamos con el fin de demostrar la excentricidad. [8]. Sin embargo, con todo esto, estos [9] [el arco KL y el arco LM] subtienden los arcos AB y BG de la excéntrica media, que no son dados; y si unimos NSE, NTZ, NHY, nuevamente encontramos que los arcos EZ y ZH de la excéntrica [ecuante] son subtendidos por los arcos ST y TY de la eclíptica, que, obviamente, ambos no son dados. Por consiguiente los arcos de las diferencias [10], KS, LT y MY, primero deben ser dados, con el fin de llevar a cabo una demostración rigurosa de la proporción de la excentricidad comenzando desde los arcos correspondientes, EZ, ZH, y ST, TY. Pero estos últimos [los arcos ST y TY] no pueden ser determinados precisamente hasta que hayamos hallado la proporción de la excentricidad y [la posición del] apogeo; no obstante, incluso sin la previa determinación precisa de la excentricidad y del apogeo, los arcos son aproximadamente dados, ya que los arcos de las diferencias no son mayores. Por lo tanto primero llevaremos a cabo los cálculos como si los [11] arcos ST, TY no difieren significativamente de los arcos KL, LM.
Para ello [Ver Fig. 10.8] sea ABG la excéntrica del movimiento medio de Marte, sobre la cual A es tomado como el punto de la primera oposición, B de la segunda, y G de la tercera. Dentro [de tal] excéntrica tomar D como centro de la eclíptica, que es nuestro punto de vista, dibujar en cada caso [donde uno tenga que llevar a cabo este tipo de cálculo] las líneas uniendo los puntos de las tres oposiciones hasta el observador (aquí entonces AD, BD y GD), y, como regla universal, prolongar una de las tres líneas dibujada [de tal manera] para encontrarse con la circunferencia de la excéntrica sobre el otro lado (aquí como GDE), y dibujar la línea uniendo los otros dos puntos opuestos (como en este caso AB). Entonces, desde el punto donde la línea recta prolongada interseca la excéntrica (en E), dibujar las líneas uniéndolas a los otros dos puntos opuestos (aquí como las [líneas] EA y EB), y eliminar las perpendiculares [desde el punto correspondiente a E] hasta las líneas uniendo los dos puntos arriba mencionados hasta el centro de la eclíptica (en este caso, eliminar EZ hasta AD, y EH hasta BD). También, eliminar una perpendicular desde uno de esos dos puntos hasta la línea uniendo el otro con un punto extra generado [(creado)] sobre la excéntrica (como aquí, la perpendicular AΘ hasta la línea BE). Si siempre observamos las reglas anteriores cuando dibujamos este tipo de figura, encontraremos que resultan las mismas proporciones numéricas, sin embargo, decidimos dibujarla [12]. El resto de la demostración se pondrá de manifiesto de la siguiente manera, sobre la base de los arcos anteriores para Marte.
Dado que el arco BG de la excéntrica esta dado subtendiendo 93;44º de la eclíptica, el ángulo en el centro de la eclíptica,
^ BDG = 93;44º donde 4 ángulos rectos = 360º
^ BDG = 187;28º donde 2 ángulos rectos = 360ºº,
y su ángulo suplementario, el ^ EDH = 172;32ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DEH,
arco EH = 172;32º
y EH = 119;45p donde la hipotenusa DE = 120p.
Similarmente, dado que el arco BG = 95;28º
El ángulo en la circunferencia, el ^ BEG = 95;28ºº donde 2 ángulos rectos = 360ºº.
Pero encontramos que el ^ BDE = 172;32ºº en las mismas unidades.
Por lo tanto el ángulo restante [en el triángulo BDE],
el ^ EBH = 92ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo BEH,
arco EH = 92º
y EH = 86;19p donde la hipotenusa BE = 120p.
Por lo tanto donde EH, como demostramos, es de 119;45p, y ED = 120p,
BE = 166;29p.
Nuevamente, dado que todo el arco ABG de la excéntrica esta dado como subtendiendo [93;44º + 67;50º =] 161;34º de la eclíptica (la suma de ambos intervalos),
el ^ ADG = 161;34º donde 4 ángulos rectos = 360º,
y, por sustracción [de 180º],
el ^ ADE = 18;26º donde 4 ángulos rectos = 360º
el ^ ADE = 36;52ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DEZ,
arco EZ = 36;52º
y EZ = 37;57p donde la hipotenusa DE = 120p.
Similarmente, dado que el arco ABG de la excéntrica, por adición [de 81;44º a 95;28º], 177;12º.
el ^ AEG = 177;12ºº donde 2 ángulos rectos = 360ºº.
Pero encontramos que el ^ ADE = 36;52ºº en las mismas unidades.
Por consiguiente el ángulo restante [en el triángulo ADE],
el ^ DAE = 145;56ºº en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AEZ,
arco EZ = 145;56º
y EZ = 114;44p donde la hipotenusa AE = 120p.
Por lo tanto, donde EZ, fue demostrado = 37;57p, y ED = 120p,
AE = 39;42p.
Nuevamente, dado que el arco AB de la excéntrica = 81;44º,
el ^ AEB = 81;44ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo AEΘ,
arco AΘ = 81;44º
y arco EΘ = 98;16º (suplementario).
Por lo tanto las cuerdas correspondientes
AΘ = 78;31p donde la hipotenusa AE = 120p
y EΘ = 90;45p donde la hipotenusa AE = 120p.
Por lo tanto donde AE, fue demostrado, ser de 39;42p, y DE esta dado como de 120p,
ΘA = 25;58p
y EΘ = 30;2p.
Pero la línea total EB fue mostrada ser de 166;29p en las mismas unidades.
Por lo tanto, por sustracción, ΘB = 136;27p donde ΘA = 25;58p.
Y ΘB² = 18615;16 [13],
ΘA² = 674;16,
entonces AB² = ΘB² + ΘA² = 19289;32.
En consecuencia AB = 138;53p donde ED = 120p y AE = 39;42p.
Pero, donde el diámetro de la Excéntrica es de 120p, AB = 78;31p,
dado que este subtiende un arco de 81;44º.
Por lo tanto donde AB = 78;31p, y el diámetro de la excéntrica es de 120p,
ED = 67;50p
y AE = 22;44p.
Por lo tanto el arco AE de la excéntrica es de 21;41º [14].
Y, por adición, el arco EABG = [177;12º + 21;41º =] 198;53°. Por lo tanto el arco restante GE = 161;7º y la cuerda correspondiente GE = 118;22p donde el diámetro de la excéntrica es de 120p.
Ahora si GE ha sido encontrado [ser] igual al diámetro de la excéntrica, es obvio que el centro podría ubicarse en GE, y la proporción de la Excentricidad inmediatamente podría ser aparente. Pero, dado que no es igual [al diámetro], sino hace que el segmento EABG [sea] mayor que un semicírculo, esta claro que el centro de la excéntrica caerá [(se ubicará)] dentro [15] de este último. Sea este en K [Fig. 10.9], y dibujar a través de D y K el diámetro a través de ambos centros, LKDM, y eliminar la perpendicular KNX desde K hasta GE.
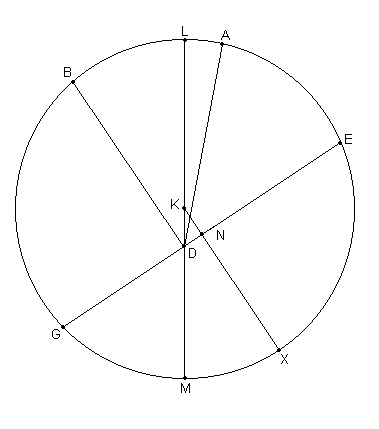
Entonces, ya que, como demostramos, EG = 118;22p donde el diámetro LM = 120p,
y DE = 67;50p en las mismas unidades,
por sustracción, GD = 50;32p en las mismas unidades.
Entonces, dado que ED * DG = LD * DM [16],
LD * DM = [67;50 * 50;32 =] 3427;51.
Pero (LD * DM) + DK² es igual al cuadrado de la mitad de toda la línea [LD + DM] [17],
por ej. (LD * DM) + DK² = LK².
Ahora el cuadrado de la mitad es de 3600, y (LD * DM) = 3427;51,
entonces DK² = 3600 - 3427;51 = 172;9,
y la distancia entre los centros,
DK ≈ 13;7p donde el radio de la excéntrica, KL = 60p [18].
Además, dado que
GN = ½ * GE = 59;11p donde el diámetro LM = 120p,
y, como demostramos, GD = 50;32p en las mismas unidades,
por sustracción, DN = 8;39p donde DK fue calculado como de 13;7p.
Por lo tanto en el círculo en el triángulo rectángulo DKN,
DN = 79;8p donde la hipotenusa DK = 120p,
y arco DN = 82;30º.
En consecuencia ^ DKN = 82;30º donde 2 ángulos rectos = 360ºº
En consecuencia ^ DKN = 41;15º donde 4 ángulos rectos = 360º.
Y dado que el ^ DKN es un ángulo [con vértice] en el centro de la excéntrica,
el arco MX = 41;15º [lo está] también.
Pero todo el arco GMX = ½ * arco GXE [= ½ * 161;7º] = 80;34º.
Por lo tanto, por sustracción, el arco a partir de la tercera oposición hasta el perigeo,
arco GM = 39;19º [19].
Y es obvio que, dado que el arco BG esta dado como de 95;28º,
por sustracción, el arco desde el apogeo hasta la segunda oposición,
arco LB [= 180º - (95;28º + 39;19º)] = 45;13º,
así que, ya que el arco AB esta dado como de 81;44º,
por sustracción, el arco desde la primera oposición al apogeo,
arco AL [= arco AB - arco LB] = 36;31º.
Tomando las cantidades de arriba como dadas, investiguemos las diferencias que se pueden derivar desde ellas en los arcos eclípticos que buscamos determinar en cada una de las oposiciones [a su vez]. Nuestra investigación procede de la siguiente manera.
[Ver fig. 10.10] En la figura previa [10.7], para las tres oposiciones, dibujemos separadamente la parte representando la primera oposición, dibujar la línea adicional AD, y eliminar la perpendicular DF y la NQ desde los puntos D y N hasta prolongación de AΘ.
Entonces, dado que arco XE = 36;31º,
^ EΘX = 36;31º donde 4 ángulos rectos = 360º
^ EΘX = 73;2ºº donde 2 ángulos rectos = 360ºº.
Y el ángulo verticalmente opuesto DΘF = 73;2ºº también en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DΘF,
arco DF = 73;2º
y arco ΘF = 106;58º (suplementario).
Por lo tanto las cuerdas correspondientes
DF = 71;25p donde la hipotenusa DΘ = 120p
y FΘ = 96;27p donde la hipotenusa DΘ = 120p.
Por lo tanto donde DΘ = 6;33 ½p y el radio de la excéntrica, DA = 60p,
DF = 3;54p
y FΘ = 5;16p.
Y ya que DA² - DF² = FA²,
AF = 59;52p,
y, dado que QF = FΘ,
por adición [de QF a FA], QA = 65;8p
donde NQ = 2 * DF = 7;48p.
Por lo tanto la hipotenusa [del triángulo rectángulo NAQ]
NA = 65;36p en las mismas unidades.
Por lo tanto, donde NA = 120p, NQ = 14;16p,
y, en el círculo alrededor del triángulo rectángulo ANQ,
arco NQ = 13;40º
en consecuencia el ^ NAQ = 13;40ºº donde 2 ángulos rectos = 360ºº.
Nuevamente, dado que QN fue demostrada ser de 7;48p y QΘ [= 2 * FΘ] ser de 10;32p,
donde el radio de la Excéntrica, ΘE = 60p,
por adición, QΘE = 70;32p en las mismas unidades,
y por lo tanto la hipotenusa [del triángulo rectángulo QNE]
NE ≈ 71p en las mismas unidades.
Por lo tanto, donde NE = 120p, QN = 13;10p, [20]
y, en el círculo alrededor del triángulo rectángulo ENQ,
arco QN = 12;36º.
En consecuencia el ^ NEQ = 12;36ºº donde 2 ángulos rectángulos = 360°°.
Pero encontramos que el ^ NAQ = 13;40ºº en las mismas unidades.
Por lo tanto, por sustracción [del ^ NEQ al ^ NAQ],
^ ANE = 1;4ºº donde 2 ángulos rectos = 360ºº
^ ANE = 0;32º donde 4 ángulos rectos = 360º.
Este [0;32º], entonces, es la cantidad del arco KS de la eclíptica.
Seguidamente, dibujemos una figura similar conteniendo [parte] del diagrama para la segunda oposición [Fig. 10.11].
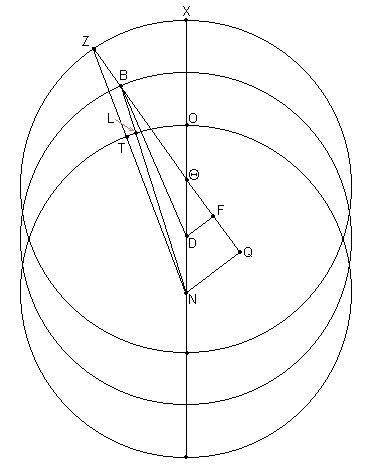
Entonces, dado que el arco XZ esta dado como de 45;13º [21],
el ^ XΘZ = 45;13º donde 4 ángulos rectos = 360º
el ^ XΘZ = 90;26ºº donde 2 ángulos rectos = 360ºº,
Y el ángulo verticalmente opuesto DΘF = 90;26ºº también en las mismas unidades.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DΘF,
arco DF = 90;26º
y arco FΘ = 89;34º (suplementario).
Por lo tanto las cuerdas correspondientes
DF = 85;10p donde la hipotenusa DΘ = 120p
y FΘ = 84;32p donde la hipotenusa DΘ = 120p.
Por lo tanto donde DΘ = 6;33 ½p y el radio de la excéntrica, DB = 60p,
DF = 4;39p
y FΘ = 4;38p.
Y dado que DB² - DF² = BF²,
FB = 59;49p,
y, dado que FQ = FΘ,
por adición, QB = 64;27p donde NQ (= 2 * DF) es calculado como de 9;18p.
Por lo tanto la hipotenusa [del triángulo rectángulo NQB]
NB = 65;6p [22] en las mismas unidades.
Por lo tanto, donde NB = 120p, NQ = 17;9p,
y, en el círculo alrededor del triángulo rectángulo BNQ,
arco NQ = 16;26º
en consecuencia el ^ NBQ = 16;26ºº donde 2 ángulos rectos = 360ºº.
Nuevamente, ya que NQ fue demostrado ser de 9;18p, y QΘ [= 2 * FΘ] = 9;16p,
donde el radio de la excéntrica, ZΘ = 60p,
por adición, QΘZ = 69;16p en las mismas unidades.
Por lo tanto la hipotenusa NZ [del triángulo rectángulo NQZ] = 69;52p. Por lo tanto, donde la hipotenusa NZ = 120p, NQ ≈ 16p, y, en el círculo alrededor del triángulo ZNQ,
arco NQ = 15;20º.
En consecuencia ^ NZQ = 15;20ºº donde 2 ángulos rectos = 360ºº.
Pero encontramos que el ^ NBQ = 16;26ºº en las mismas unidades.
Por lo tanto, por sustracción, el ^ BNZ = 1;6ºº en las mismas unidades. Por lo tanto, por sustracción, el ^ BNZ = 0;33º donde 4 ángulos rectos = 360º.
Estos [0;33º], entonces, es la cantidad del arco LT de la eclíptica.
Ahora, dado que encontramos el arco KS como 0;32º para la primera oposición, es claro que el primer intervalo, tomado con respecto a la excéntrica [23], será mayor respecto del intervalo del movimiento aparente por la suma de ambos arcos, [a saber] de 1;5º, y [por lo tanto] contendrá 68;55º.
Entonces, sea [parte] del diagrama para que la tercera oposición sea dibujada [Fig. 10.12]. Ahora, dado que el arco PH esta dado como 39;19º,
el ^ PΘH = 39;19º donde 4 ángulos rectos = 360º
el ^ PΘH = 78;38ºº donde 2 ángulos rectos = 360ºº.
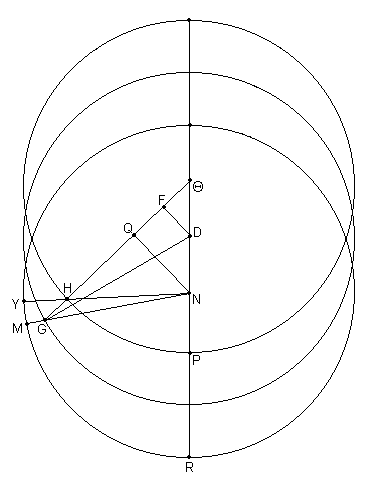
Por lo tanto, en el círculo alrededor del triángulo rectángulo DΘF,
arco DF = 78;38º
y arco ΘF = 101;22º (suplementario).
Por lo tanto las cuerdas correspondientes
DF = 76;2p donde la hipotenusa DΘ = 120p
y ΘF = 92;50p donde la hipotenusa DΘ = 120p.
Por lo tanto donde la distancia entre los centros, DΘ = 6;33 ½p, y el radio de la excéntrica, DG = 60p,
DF = 4;9p
y ΘF = 5;4p.
Y dado que GD² - DF² = GF²,
GF = 59;51p,
y, dado que ΘF = FQ,
por sustracción, GQ = 54;47p donde NQ (= 2 * DF) esta calculada como de 8;18p.
Por consiguiente la hipotenusa [del triángulo rectángulo NGQ]
NG = 55;25P en las mismas unidades.
Por lo tanto, donde NG = 120p, NQ = 17;59p,
y, en el círculo alrededor del triángulo rectángulo GNQ,
arco NQ = 17;14º
en consecuencia ^ NGQ = 17;14ºº donde 2 ángulos rectos = 360ºº.
Nuevamente, dado que NQ fue demostrado ser de 8;18p, y ΘQ [= 2 * FΘ] = 10;8p,
donde el radio de la excéntrica, ΘH = 60p,
por sustracción, QH = 49;52p en las mismas unidades,
y por lo tanto la hipotenusa NH [del triángulo rectángulo NHQ] = 50;33p.
Por lo tanto, donde NH = 120p, NQ = 19;42p,
y, en el círculo alrededor del triángulo rectángulo HNQ,
arco NQ = 18;54º.
En consecuencia el ^ NHQ = 18;54ºº donde 2 ángulos rectos = 360ºº.
Pero demostramos que el ^ NGQ = 17;14ºº en las misas unidades.
Por lo tanto por sustracción, el ^ GNH = 1;40ºº en las mismas unidades. Por lo tanto por sustracción, el ^ GNH = 0;50º donde 4 ángulos rectos = 360º.
Estos [0;50º], entonces, es la cantidad del arco MY de la eclíptica.
Ahora dado que hallamos el arco LT como de 0;33º para la segunda oposición, esta claro que el segundo intervalo, tomado con respecto a la excéntrica, será menor que el intervalo del movimiento aparente por la suma de ambos arcos, [a saber] 1;23º, y [de este modo] contendrá 92;21º.
Utilizando los arcos eclípticos así calculados para los dos intervalos, y, una vez más, los arcos originales asumidos para la excéntrica [ecuante], y siguiendo el teorema demostrado anteriormente [Figs. 10.8 a 10.9] para tales elementos, por medio de los cuales determinamos [la posición del] apogeo y la proporción de la excentricidad, hallamos (no para extender nuestras descripciones otra vez con la ayuda de los mismos cálculos en detalle),
la distancia entre los centros, DK = 11;50p donde el radio de la excéntrica es de 60p;
el arco de la excéntrica desde la tercera oposición hasta el perigeo, GM = 45;33º [24].
Por lo tanto arco LB = [180º - (95;28º + 45;33º)] = 38;59º
y arco AL = [81;44º - 38;59º] = 42;45º.
A continuación, empezando desde estos [arcos] como datos, encontramos desde nuestra demostración para cada una de las oposiciones [de manera separada] las siguientes cantidades para el tamaño verdadero de cada uno de los arcos en cuestión:
arco KS 0;28º
arco LT, alrededor de la misma [cantidad], 0;28º
y arco MY 0;40 [25].
Combinamos las [correcciones] para la primera y la segunda oposición, sumando el resultado de 0;56º al arco eclíptico del primer intervalo, 67;50º, y tomado el intervalo preciso con respecto a la excéntrica como de 68;46º. Nuevamente, combinando las [correcciones] para la segunda y la tercera oposición, y sustrayendo el resultado de 1;8º desde el movimiento aparente sobre la eclíptica sobre el segundo intervalo, 93;44º, tomamos el intervalo preciso con respecto a la excéntrica como de 92;36º.
Seguido, utilizando el mismo procedimiento [como el anterior], determinamos un valor más preciso para la razón de la excentricidad y [la posición del] apogeo; encontramos la distancia entre los centros, DK ≈ 12p donde el radio de la Excéntrica,
KL = 60p,
arco GM de la excéntrica = 44;21º [26],
por consiguiente, nuevamente, el arco LB = 40;11º
y arco AL = 41;33º.
A continuación, demostraremos por medio de las mismas [configuraciones] que los intervalos aparentes observados entre las tres oposiciones son encontrados estar de acuerdo con las cantidades de anteriores.
Sea allí dibujado [Fig. 10.13] el diagrama para la primera oposición, aunque solamente con la Excéntrica EZ, sobre la cual se dibuja el centro del Epiciclo [que] siempre es transportado.
Luego
el ^ AΘE = 41;33º donde 4 ángulos rectos = 360º,
entonces donde 2 ángulos rectos = 360ºº,
el ^ AΘE = 83;6ºº = ^ DΘF (verticalmente opuesto).
Por lo tanto, en el círculo alrededor del triángulo rectángulo DΘF,
arco DF = 83;6º
y arco FΘ = 96;54º (suplementario).
Por lo tanto las cuerdas correspondientes
DF = 79;35p donde la hipotenusa DΘ = 120p
y FΘ = 89;50p donde la hipotenusa DΘ = 120p.
Por lo tanto donde DΘ = 6p y la hipotenusa [del triángulo rectángulo DAF] DA = 60p,
DF = 3;58 ½p
y FΘ = 4;30p.
Y dado que DA² - DF² = FA²,
FA = 59;50p en las mismas unidades.
Además, dado que FΘ = FQ y NQ = 2 * DF,
por adición, AQ = 64;20p donde NQ = 7;57p.
Por lo tanto la hipotenusa [del triángulo rectángulo NAQ] NA = 64;52p en las mismas unidades.
Por lo tanto donde NA = 120p, NQ = 14;44p,
y, en el círculo alrededor del triángulo rectángulo ANQ,
arco NQ = 14;6º.
En consecuencia el ^ NAQ = 14;6ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ NAQ = 7;3º donde 4 ángulos rectos = 360º.
Pero el ^ AΘE = 41;33º en las mismas unidades.
Por lo tanto, por sustracción, el ángulo de la posición aparente, el ^ ANE = 34;30º. Esta es la cantidad por la cual el planeta [se ubicó] por delante del apogeo en la primera oposición.
Sea un diagrama similar [Fig. 10.14] dibujado nuevamente para la segunda oposición. Entonces el ángulo de la posición media del epiciclo,
el ^ BΘE = 40;11º donde 4 ángulos rectos = 360º,
entonces donde 2 ángulos rectos = 360ºº,
el ^ BΘE = 80;22ºº = ^ QΘN (verticalmente opuesto).
Por lo tanto, en el círculo alrededor del triángulo DΘF,
arco DF = 80;22º
y arco FΘ = 99;38º (suplementario).
Por lo tanto las cuerdas correspondientes
DF = 77;26p donde la hipotenusa DΘ = 120p
y FΘ = 91;41p donde la hipotenusa DΘ = 120p.
Por lo tanto donde DΘ = 6p y la hipotenusa [del triángulo rectángulo DBF] DB = 60p,
DF = 3;52p
y FΘ = 4;35p.
Y dado que DB² - DF² = BF²,
BF = 59;53p en las mismas unidades.
Y, por el mismo argumento [como el anterior] [27],
dado que FΘ = FQ, y NQ = 2 * DF,
por adición, BQ = 64;28p donde NQ = 7;44p.
Por lo tanto la hipotenusa [del triángulo rectángulo BNQ] BN = 64;56p en las mismas unidades. Por lo tanto, donde la hipotenusa BN = 120p, NQ = 14;19p [28], y, en el círculo alrededor del triángulo rectángulo BNQ,
arco NQ = 13;42º.
En consecuencia el ^ NBQ = 13;42ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ NBQ = 6;51º donde 4 ángulos rectos = 360º.
Pero el ^ BΘE = 40;11º en las mismas unidades.
Por lo tanto, por sustracción, el ángulo de la posición aparente,
^ ENB = 33;20º en las mismas unidades.
Estos [33;20º], entonces, es la cantidad por la que el planeta, en su movimiento aparente, estuvo hacia atrás del apogeo en la segunda oposición. Y demostramos que en la primera oposición este estuvo 34;30º hacia adelante del apogeo. Por lo tanto la distancia total [en el movimiento aparente] desde la primera hasta la segunda oposición llega a ser de 67;50º, de acuerdo con lo que derivamos de las observaciones [Fig. 10.7].
Sea el diagrama [Fig. 10.15] para la tercera oposición dibujado del mismo modo. En este caso el ángulo de la posición media del epiciclo,
el ^ GΘZ = 44;21º donde 4 ángulos rectos = 360º
el ^ GΘZ = 88;42ºº donde 2 ángulos rectos = 360ºº.
Por lo tanto, en el círculo alrededor del triángulo rectángulo DΘF,
arco DF = 88;42º
y arco FΘ = 91;18º (suplementario).
Por lo tanto las cuerdas correspondientes
DF = 83;53p donde la hipotenusa DΘ = 120p
y FΘ = 85;49p donde la hipotenusa DΘ = 120p.
Por lo tanto donde DΘ = 6p y el radio de la excéntrica, DG = 60p,
DF = 4;11 ½p
y FΘ = 4;17p.
Y dado que DG² - DF² = GF²,
encontramos que GF = 59;51p en las mismas unidades.
Además, dado que FΘ = FQ, y NQ = 2 * DF,
Encontramos por sustracción que QG = 55;34p donde NQ = 8;23p.
Por consiguiente encontramos que la hipotenusa [del triángulo rectángulo GNQ]
GN = 56;12p en las mismas unidades.
Por lo tanto, donde la hipotenusa GN = 120p, NQ = 17;55p, y, en el círculo alrededor del triángulo rectángulo GNQ,
arco NQ = 17;10º.
En consecuencia el ^ ΘGN = 17;10ºº donde 2 ángulos rectos = 360ºº
En consecuencia el ^ ΘGN = 8;35º donde 4 ángulos rectos = 360º.
Pero el ^ GΘZ = 44;21º en las mismas unidades.
Por lo tanto, por adición, el ^ GNZ = 52;56º en las mismas unidades.
Estos [52;56º], entonces, es la cantidad por la cuál el planeta estuvo por delante del perigeo en la tercera oposición. Pero también demostramos que en la segunda oposición este estuvo a 33;20º hacia atrás del apogeo. Así que hemos encontrado 93;44º entre la segunda y tercera oposición, calculado por sustracción [de la suma de 52;56º y 33;20º desde los 180º], de acuerdo con la cantidad observada en el segundo intervalo [Fig. 10.7].
Además, dado que el planeta, cuando es observado en la tercera oposición a lo largo de la línea GN, tuvo una longitud de ♐︎ 2;34º de acuerdo con nuestra observación [al comienzo de este capítulo], y el ángulo GNZ [ubicado] en el centro de la eclíptica fue demostrado ser de 52;56º, esta claro que el perigeo de la excéntrica, en el punto Z, tiene una longitud de (♐︎ 2;34º + 52;56º =] ♑︎ 25;30º, mientras el apogeo estuvo diametralmente opuesto a ♋︎ 25;30º.
Y si dibujamos [ver. Fig. 10.16] el epiciclo KLM de Marte sobre el centro G y prolongamos la línea ΘGM [29], tendremos, en el momento de la tercera oposición:
el movimiento medio del epiciclo contado desde el apogeo de la excéntrica: 135;39º (dado que su ángulo suplementario, el ^ GΘZ, fue demostrado ser de 44;21º);
el movimiento medio del planeta desde el apogeo del epiciclo M (por ej. el arco MK): 171;25º (dado que el ^ ΘGN fue demostrado [anteriormente] ser de 8;35º, y dado que este es un ángulo [con su vértice] en el centro del epiciclo, el arco KL desde el planeta en K hasta el perigeo en L es también de 8;35º, por consiguiente el arco suplementario desde el apogeo M hasta el planeta en K es, como ya esta establecido, de 171;25º).
Por consiguiente hemos demostrado, entre otras cosas, que en el momento de la tercera oposición; por ej. en el segundo año de Antonino Pío, 12/13 de Epiphi en el calendario Egipcio, 2 horas equinocciales antes de la medianoche, las posiciones medias del planeta Marte fueron:
En longitud (así llamada) desde el apogeo de la excéntrica: 135;39º
En anomalía desde el apogeo del epiciclo: 171;25º
Lo que se ha requerido para examinar.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro X |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Ver HAMA 172-7, Pedersen 273-83, sobre el método utilizado para hallar las excentricidades de los planetas exteriores.
- ↑ Leer (en los manuscritos D, G y Ar) en cambio de "elongación" en H322,1.
- ↑ Se llegan a las horas por el cálculo de la posición media del Sol. Por consiguiente la posición media del Sol calculada en la hora establecida debería ser exactamente 180º diferente a las longitudes dadas. Encuentro, desde las tablas del movimiento solar medio, 260;58,55º (en cambio de 261º), 328;50,22º (en cambio de 328;50º) y 62;31,45º (en cambio de 62;34º). Estas últimas discrepancias representan alrededor de media hora en el movimiento solar. ¿Pudo Ptolomeo haber aplicado aquí la ecuación del tiempo (siendo alrededor de -25 ½ minutos comparados con el valor de la época)? Si esto fuera así, estuvo errado, ya que todos los cálculos son en términos de días solares medios.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Marte en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Marte Latitud de Marte Elongación Altura Azimut Magnitud Marte en Carta 15 de diciembre de 130 d. C. (130) 01:00 h ♐︎ 262° 27' 07" ♊︎ 81° 35' 21" +03° 26' 54" E 176° 26' 12" 75° 01' 27" 77° 14' 46" -1,4 Gemini 
Almagesto Observación 15.12.130 d. C. En ese instante, Marte se encontraba a: 3° 57' 21" (NNW) de Delta Gemini (Wasat, “el medio o centro del cielo”).
La oposición de Marte ocurrió el 14 de diciembre de 130 d. C. (130) a las 10:23:07 hora local. Ese mismo día pasaba por el meridiano del lugar a las 23:54:36, altura: 85° 38' y azimut: 0°. Distancia Tierra-Marte: 92.206.838,01 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Marte en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Marte Latitud de Marte Elongación Altura Azimut Magnitud Marte en Carta 21 de febrero de 135 d. C. (135) 21:00 ♓︎ 331° 54' 07" ♍︎ 150° 23' 33" +04° 15' 27" E 175° 29' 11" 42° 34' 35" 277° 43' 00" -1,3 Virgo 
Almagesto Observación 21.02.135 d. C. En ese instante, Marte se encontraba a: 3° 38' 49" (NNE) de Beta Virgo (Zavijava, “el rincón del perro que ladra”).
La oposición de Marte ocurrió el 20 de febrero de 135 d. C. (135) a las 18:54:22 hora local. Ese mismo día pasaba por el meridiano del lugar a las 00:26:59, altura: 73° 58' y azimut: 0°. Distancia Tierra-Marte: 96.795.967,65 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Fecha y horas calculadas con un programa de computación desde la observación realizada por Ptolomeo (actual Alejandría) de la siguiente:
Oposición de Marte en el día de la observación de Ptolomeo Fecha Hora Longitud del Sol Longitud de Marte Latitud de Marte Elongación Altura Azimut Magnitud Marte en Carta 27 de mayo de 139 d. C. (139) 22:00 ♉︎ 63° 53' 45" ♐︎ 243° 05' 25" -03° 01' 21" E 176° 52' 56" 29° 11' 27" 331° 51' 10" -2,6 Sagittarius 
Almagesto Observación 27.05.139 d. C. En ese instante, Marte se encontraba a: 4° 25' 55" (NNW) de Gama Sagittarius (Al Nasl, “la punta de la flecha”), a 06° 22' 19" (NW) de Delta Sagittarius (Kaus Meridionalis, "la del centro del Arco") y a 07° 21' 07" (W) de Lambda Sagittarius (Kaus Borealis, "la parte Norte del arco").
La oposición de Marte ocurrió el 27 de mayo de 139 d. C. (139) a las 07:20:23 hora local. Ese mismo día pasaba por el meridiano del lugar a las 23:46:46, altura: 34° 50' y azimut: 0°. Distancia Tierra-Marte: 63.549.047,05 kms.
Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Ptolomeo se esta refiriendo a los períodos poco exactos en el Libro IX Capítulo 3. Por consiguiente para Marte (cf. en la tabla "Vueltas en Anomalía") en 79 años solares ocurrieron 37 vueltas en anomalía y 42 vueltas en longitud. Asumiendo la longitud del año de Ptolomeo de 365;14,48 días, uno encuentra desde este [valor], para 4 años 69 días 20 horas, un incremento longitudinal de 81;39º, y, para 4 años 96 días 1 hora, 95;23º. Utilizando el procedimiento de Ptolomeo, y llevando a cabo las tres iteraciones, encuentro desde los datos anteriores: 2 * e ≈ 11;57p, distancia de la 3 er. oposición desde el perigeo ≈ 44º. Comparando los resultados de Ptolomeo con datos más precisos, de 12p y 44;21º, demuestran que las diferencias son incluso insignificantes.
- ↑ La situación podría ser idéntica con aquella de la hipótesis de la Luna (Libro IV Capítulo 6).
- ↑ Leer (en los manuscritos A y B (no reportada por Heiberg) y Ar) en cambio de en H324,8.
- ↑ Los arcos que forman las diferencias entre el arco KL y el arco TS, y entre el arco LM y el arco TY.
- ↑ Leer παρά , en H324,22, en cambio de παρά ("como si los arcos no difieren significativamente de [los arcos] KLM y STY", lo cuál no tiene sentido). Mi texto es la lectura en todos los manuscritos, Griegos y Arábigos. Heiberg omitió a través de un desliz o un error de impresión. Dado que Manitius no se dio cuenta de ello, su traducción aquí tiene graves deficiencias.
- ↑ Por ej. cualquiera de las líneas AD, BD, GD que decidimos prolongar.
- ↑ El cuadrado de 136;27 es 18618;36 al minuto más cercano. El error no tiene un efecto significativo sobre el tamaño posterior de AB.
- ↑ Aquí hay algunos serios errores. Dado que para la cuerda AE uno debería encontrar, desde las figuras de Ptolomeo, 22;27p, y este [valor] es incluso la lectura en el manuscrito de Gerardo de Cremona (aunque no el resto de la tradición Árabe) en H329,6. Sin embargo, el arco de esta última [cuerda AE], no es de 21;41º, sino de 21;34º. El resultado de Ptolomeo [de] 21;41º (confirmado por sus cálculos posteriores), es el arco de 22;34p. Parece como si los errores son propios de Ptolomeo (por consiguiente la lectura del manuscrito de Gerardo de Cremona es una enmienda equivocada). ¿Ptolomeo calculó 22;27p → 21;34º, y entonces, mal interpretó sus propias notas, 22;34p → 21;41º?.
- ↑ Leer (en los manuscritos D y G) en H329,17 en cambio de ("en el último"). Corregido por Manitius.
- ↑ Euclides III 35.
- ↑ Euclides II 5.
- ↑ Un cálculo preciso a partir de los datos originales de Ptolomeo da alrededor de 13;2 ½p.
- ↑ Un cálculo preciso a partir de los datos de Ptolomeo da 39;10º.
- ↑ Aquí los redondeos son particularmente imprecisos: uno encuentra a partir de los números inmediatamente anteriores que NE = 70;57,48p, por consiguiente QN = 13;11,24p. Incluso NE = 71p nos lleva a QN = 13;10,59p.
- ↑ Cf. arco LB en la Fig. 10.10.
- ↑ Leer seg. ξε (en los manuscritos D y Ar) en cambio de seg. ξθ (69;6) en H335,9. La corrección es validada por los cálculos precedentes y posteriores.
- ↑ Por ej. la ecuante: esto esta realizado explícitamente en Libro XI Capítulo 1, nota de referencia nro. 10 (cálculos siguientes a la Fig. 11.15).
- ↑ A partir de los elementos de Ptolomeo, ∆ seg. λ1 = 81;44°, ∆ seg. λ2 = 95;28º, ∆ λ1 = 68;55º, ∆ λ2 = 92;21º, yo calculo 2 * e = 11;50p, GM = 45;28º.
- ↑ A partir de una doble Excentricidad de 11;50p y los valores de Ptolomeo para los arcos GM, LB y AL, encuentro: el arco KS = 0;2,49º, arco LT = 0;26,51º , arco = MY 0;39,31º.
- ↑ Encuentro desde los elementos de Ptolomeo: DK = 11;59,50p ≈ 12p, arco GM = 44;18,45º ≈ 44;19º. Ptolomeo esta completamente en lo correcto para terminar aquí con sus cálculos, dado que una iteración posterior prolonga un cambio en la Excentricidad de menos de 0;0,30p y en la línea de los ápsides menos de 5'.
- ↑ Leer (en el manuscrito D, , Ar) en cambio de ("de acuerdo a esto") en H342,23.
- ↑ 7;44 * 120 / 64;56 = 14;17,30, aunque si uno lleva los cálculos anteriores a dos lugares fraccionarios sexagesimales, encuentra NQ = 14;18,41p. A menudo, Ptolomeo calcula con mayor precisión de lo que el texto implica.
- ↑ Leer ΘGM (en el manuscrito de Al-Ḥajjāj ibn Yūsuf ibn Maṭar) en cambio de ΘG (ΘG) en H345,22.
