Almagesto: Libro X - Capítulo 06
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Preliminares para las demostraciones concernientes a los otros [3] Planetas [Exteriores]}
Tales fueron, entonces, los métodos que utilizamos acertadamente para esos dos planetas, Mercurio y Venus, [y] para establecer las hipótesis y demostrar [los valores de] las anomalías. Dado que para los otros tres [planetas], Marte, Júpiter y Saturno, la hipótesis que hemos hallado para sus movimientos es la misma [que para todos ellos] e igual a aquella establecida para el planeta Venus, a saber, una en la que la Excéntrica sobre la cual el centro del Epiciclo siempre es transportado esta descripta sobre un centro que es el punto bisecando (dividiendo en dos) la línea que une el centro de la Eclíptica y el punto alrededor del cual el epiciclo tiene su movimiento uniforme; ya que también en el caso de cada uno de esos planetas, la excentricidad que uno encuentra desde la máxima ecuación de la anomalía eclíptica utilizando una estimación aproximada [(bastante tosca)], resulta ser aproximadamente el doble de aquella derivada del tamaño de los arcos retrógrados en las máximas y en las mínimas distancias del epiciclo. Sin embargo, las demostraciones por las cuales calculamos las cantidades tanto de las anomalías y [de las posiciones de] los apogeos no se puede proceder a lo largo de las mismas líneas para esos planetas como [(se lo hizo con)] los dos anteriores, dado que ellos alcanzan cada [una de las] elongaciones posibles desde el Sol, y esto no es obvio desde las observaciones, como lo fue en las Máximas Elongaciones de Mercurio y de Venus, [es decir] cuando el planeta se encuentra en el punto donde la línea de nuestra visión es tangente al epiciclo. Entonces, dado que esta aproximación no esta disponible, hemos utilizado observaciones desde sus oposiciones para la posición media del Sol para demostrar, primero de todo, las proporciones de sus excentricidades y [las posiciones de] sus apogeos. Porque solamente en tales posiciones [del planeta] [1], consideradas desde un punto de vista teórico, hallamos por separado la anomalía de la eclíptica, no con un efecto de la anomalía relacionada con el Sol.
Para ello sea ABG [Fig. 10.5] la excéntrica del planeta, sobre la cual el centro del epiciclo, el centro D, es transportado y sea AG el diámetro a través del apogeo, en el cuál el punto E es el centro de la eclíptica, y Z el centro de esa excéntrica con respecto al cual es tomado el movimiento medio en longitud del epiciclo. Dibujar el epiciclo HΘKL en el centro B, y unir ZLBΘ y HBKEM.
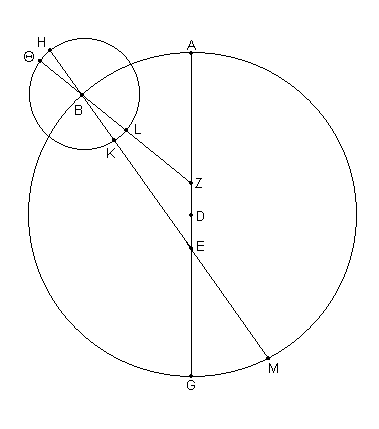
Y digo, primero, que cuando el planeta es visto a lo largo de la línea EH a través del centro del epiciclo B, entonces, también, la posición media del Sol estará sobre una misma línea, y que cuando el Sol esta en H este [(planeta)] estará en conjunción [2] con [la longitud media del] Sol (que también será visto, en teoría, hacia H), y cuando el planeta esta en K estará en oposición con [la posición] media del Sol (que será visto, en teoría, hacia M).
[Demostrar:] Para cada uno de esos planetas [exteriores], la suma de los movimientos medios en longitud y en anomalía, contados desde el apogeo [de la excéntrica y del epiciclo respectivamente], es igual al movimiento medio del Sol contado desde el mismo punto de partida. Y la diferencia entre el ángulo [(vértice ubicado)] en el centro Z (que comprende el movimiento medio del planeta en longitud) [3], y el ángulo en E (que comprende el movimiento aparente en longitud) [3], es siempre el ángulo [con vértice] en B (que comprende el movimiento medio sobre el epiciclo).
Por consiguiente esta claro que cuando el planeta esta en H, este llega a poco menos de una vuelta con el ^ HBΘ hasta el apogeo Θ; pero el ^ HBΘ sumado al ^ AZB produce el ángulo comprendiendo el movimiento medio del Sol, a saber el ^ AEH, que es el mismo como el movimiento aparente del planeta [4]. Y cuando el planeta esta en K, su movimiento sobre el epiciclo, nuevamente, será el ^ ΘBK, y el ^ ΘBK + el ^ AZB es igual al movimiento medio del Sol contado desde el apogeo A.

Así esto último comprende 180º + (^ AZB - ^ LBK) = 180º + ^ GEM, por ej. la posición media del Sol será opuesta a la posición aparente del planeta.
Por lo tanto, además, en tales configuraciones [por ej. en las conjunciones medias y en las oposiciones], la línea uniendo el centro B del epiciclo hasta el planeta, y la línea desde E, nuestro punto de vista, hasta [la posición media] del Sol, coincidirá en una línea recta, pero en todas las otras elongaciones [Sol - Planeta, estos vectores] siempre serán paralelos unos con otros, aunque variará la dirección en la que ellos apuntan.

[Demostrar:] En la figura de arriba [ver Fig. 10.6], si dibujamos la línea BN desde B hasta el planeta [ubicado] en cualquiera posición, y la línea EX desde E hasta [la posición media del] Sol, por las razones anteriormente establecidas
^ AEX = ^ AZΘ + ^ NBΘ [5],
y ^ AZΘ = ^ AEH + ^ HBΘ.
[en consecuencia ^ AEX = ^ AEH + ^ NBΘ + ^ HBΘ].
Si sustraemos ^ AEH desde ambos lados,
^ HEX = ^ HBN.
Por lo tanto la línea EX es paralela a la línea BN.
En consecuencia hallamos que en las configuraciones de las conjunciones y de las oposiciones anteriores con respecto a [la posición media del] Sol, el planeta es visto, en teoría, [a lo largo de la línea] a través del centro del epiciclo, justamente como si su movimiento sobre el epiciclo no existiera, pero en cambio como si estuviera en sí ubicado sobre el círculo ABG y transportado con un movimiento uniforme por la línea ZB, del mismo modo como lo hace el centro epiciclo. Por consiguiente esta claro que es posible separar y demostrar la proporción de la excentricidad de la eclíptica [tanto por ambos de] estos tipos de posiciones [planetarias], pero dado que las conjunciones no son visibles, nos quedan las oposiciones [6] sobre las cuales construimos nuestras demostraciones.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro X |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 |
Notas de referencia
- ↑ Ver HAMA 172. Un análisis ingenioso del camino por el cual Ptolomeo llega a la noción de Ecuante para los planetas exteriores, fue realizado por Swerdlow, "El Origen de la Teoría Planetaria Ptolemaica".
- ↑ Leer (en el manuscrito G, y posiblemente el Ar, pero las traducciones son ambiguas) en cambio de ("esta en conjunción") en H318,18.
- ↑ 3,0 3,1 Por esta expresión () Ptolomeo da a entender, no la posición verdadera del planeta, sino la posición del centro del epiciclo visto desde la Tierra. Comparar la expresión en Libro XII Capítulo 2 Fig. 12.7 (H470,11) para denotar la "anomalía verdadera" (por ej. contada desde el perigeo verdadero y no desde el perigeo medio del epiciclo).
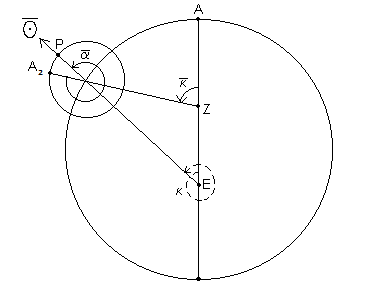
- ↑ De hecho ^ AZB - ^ HBQ = ^ AEH. Pero lo que Ptolomeo da a entender esta ilustrado en las Figs. P1 y P2: en la Fig. P1 el planeta y el [la posición media del] Sol están en conjunción. En Fig. P2 (= Fig. 10.5) están nuevamente en conjunción. El epiciclo ha recorrido [el arco] a lo largo del ángulo seg. κ (^ AZB), el planeta sobre el epiciclo ha recorrido [el arco] a lo largo del seg. α, y [la posición media del] Sol a lo largo de κ + 360º. Entonces (desde la figura) κ = seg. κ - (360º - seg. α) = seg. κ - seg. α - 360º. Por lo tanto el movimiento medio del Sol κ + 360º = seg. κ + seg. α. Al no entender esto, un "interpolador" ha insertado en H319,8, produciendo el extraño resultado: "el ^ HBΘ sumado al ^ AZB, por ej. restado de él".
- ↑ Por ej. el movimiento medio del Sol es igual al movimiento longitudinal medio del planeta más la anomalía media del planeta.
- ↑ , literalmente "configuraciones [en las que el planeta sale y se pone] al comienzo y al final de la noche".