Almagesto: Libro VI - Capítulo 05
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
{Sobre los límites Eclípticos del Sol y de la Luna}
Ahora que hemos explicado los métodos de arriba, sería apropiado seguir con las consideraciones pertinentes a los límites de la Eclíptica para ambos eclipses solares y lunares. El propósito de esto es que si decidimos calcular [en un año dado], no todas las Sizigias Medias, sino justamente aquellas que podrían caer dentro de la categoría concerniente a los pronósticos de los eclipses [2], es posible que tengamos un método práctico para decidir cuáles de esas son de las entradas para la Posición Media en Latitud de la Luna en cada sizigia media.
Ahora en el libro precedente (Libro V al final del capítulo 14) hemos demostrado que el diámetro de la Luna subtiende un arco que es de 0;31,20º del gran círculo dibujado alrededor del centro de la eclíptica en la Máxima Distancia de la Luna. Calculamos esto por medio de los dos eclipses que ocurren cerca del apogeo del Epiciclo de la Luna. Entonces ahora también, cuando nos proponemos determinar los límites máximos de las sizigias de la eclíptica (cuyos límites están determinados por la posición de la Luna en el perigeo del epiciclo) demostraremos, también en esta situación, por el mismo camino, el tamaño del arco subtendido por el diámetro de la Luna [en ese instante], por medio de dos eclipses [de esta época] de entre aquellos que han sido observados cerca del perigeo [del Epiciclo]. Para ello es más seguro demostrar este tipo de parámetro desde el presente fenómeno.
[El primero]. En el séptimo año de Filometor, que es el 574 to. año desde [el comienzo de la era de] Nabonassar, en el 27/28 de Phamenoth [VII] en el calendario Egipcio [30 de Abril / 1 de Mayo de -173], desde el comienzo de la octava hora hasta el final de la décima en Alejandría, ocurrió un eclipse de Luna que alcanzó un Máximo Oscurecimiento de 7 Dígitos desde el [limbo] Norte. Entonces el eclipse medio ocurrió 2 ½ horas de estación después de la medianoche, que corresponden a 2 ⅓ horas equinocciales, dado que la posición verdadera del Sol estuvo en ♉︎ 6 ¼º [3]. Y el tiempo desde la época [de Nabonassar] hasta el eclipse medio es de
573 años Egipcios 206 días 14 ⅓ horas equinocciales recontados simplemente
573 años Egipcios 206 días 14 horas equinocciales recontados en días solares medios.
En este momento la posición del centro de la Luna estuvo según lo siguiente:
en longitud media: ♏︎ 7;49º
en longitud media: ♏︎ 6;16º [4]
la distancia [en anomalía] desde el apogeo del epiciclo: 163;40º
la distancia desde el límite Norte sobre el círculo inclinado: 98;20º.
Por lo tanto esta claro que cuando el centro de la Luna esta a 8;20º desde el nodo (medido a lo largo del círculo inclinado), mientras la Luna esta cerca de su mínima distancia [en la sizigia], y el centro de la sombra esta sobre el gran círculo dibujado a través del centro de la Luna a ángulos rectos al círculo inclinado (que es la posición [donde ocurre] el mayor oscurecimiento), (½ + 1/12) ma. parte del diámetro de la Luna esta inmersa en la sombra [5].
[El segundo] Nuevamente, en el trigésimo séptimo año del Tercer Ciclo Calípico, que es el 607 mo. año desde [el comienzo de la era] Nabonassar, 2/3 de Tybi [V] en el calendario Egipcio [27/28 de Enero del -140], en el comienzo de la quinta hora [de la noche] en Rodas, la Luna comienza a ser eclipsada; el máximo oscurecimiento fue de 3 Dígitos desde el [limbo] Sur.
Aquí, entonces, el comienzo del eclipse fue 2 horas de estación antes de la medianoche, que corresponde a 2 ⅓ horas equinocciales en Rodas y en Alejandría, dado que la posición verdadera del Sol estuvo en ♒︎ 5;8º. Y el eclipse medio, en el cual ocurrió el máximo oscurecimiento, fue alrededor de 1 ⅚ horas equinocciales antes de la medianoche. El [período de] tiempo desde la época [de Nabonassar] hasta el eclipse medio es de
606 años Egipcios 121 días 10 ⅙ horas equinocciales, si son recontados simplemente o en Días Solares Medios.
En este momento la posición del centro de la Luna estuvo según lo siguiente:
en longitud media: ♌︎ 5;16º
en longitud verdadera: ♌︎ 5;8º [6]
la distancia [en anomalía] desde el apogeo del epiciclo: 178;46º
la distancia desde el límite Norte sobre el círculo inclinado: 280;36º.
Por lo tanto es claro que cuando el centro de la Luna esta a 10;36º desde el nodo (medido a lo largo del círculo inclinado), mientras la Luna esta (como anteriormente [explicado]) cerca de la mínima distancia, y el centro de la sombra esta en la intersección de la eclíptica con el gran círculo dibujado a través del centro de la Luna en ángulos rectos al círculo inclinado [de la Luna], entonces un cuarto del diámetro de la Luna estará inmerso en la sombra [7].
Pero [8] cuando el centro de la Luna esta a 8 ⅓º desde el nodo sobre su círculo inclinado, este (Radio de la Sombra) es de 43 1/20', medidos a lo largo del gran círculo dibujado a través de los polos del círculo inclinado, desde la eclíptica; y cuando este esta a 10 ⅗º desde el nodo sobre su círculo inclinado, es de 54 ⅚', medidos a lo largo del gran círculo dibujado a través de los polos del círculo inclinado, desde la eclíptica. Ahora la diferencia [en magnitud] entre los dos eclipses comprende ⅓ del diámetro de la Luna, y la diferencia en las dos distancias anteriores desde su centro, medida a lo largo del mismo gran círculo, desde el mismo punto de la eclíptica (por ej. desde el centro de la sombra) es de 0;11,47º. Entonces esta claro que todo el diámetro de la Luna subtiende un arco alrededor de 0;35,20º del gran círculo dibujado sobre el centro de la eclíptica en la mínima distancia de la Luna [en la sizigia].
Además, en el segundo eclipse, en el que ¼ del diámetro de la Luna fue oscurecido, el centro de la Luna estuvo a 54 ⅚' desde el centro de la sombra y ¼ del diámetro de la Luna (por ej. 8 ⅚') desde el punto en el cuál la línea uniendo los centros [de la Luna y de la sombra] interseca el perímetro de la sombra. Por lo tanto es inmediatamente obvio que, por sustracción, el radio de la sombra en la mínima distancia de la Luna es de 46'. Este es insignificantemente mayor que 2 ⅗ veces el radio de la Luna, que es de 17 ⅔'. Además, el radio del Sol subtiende 0;15,40º del gran círculo dibujado a través del Sol alrededor del centro de la eclíptica. Ya que, como demostramos (en el Libro V Capítulo 14), el Sol cubre la misma cantidad de su círculo [por ej. subtiende el mismo ángulo] como la Luna lo hace cuando esta en su mayor distancia en la sizigia. Por lo tanto, cuando el centro aparente de la Luna esta a [0;17,40 + 0;15,40 =] 0;33,20º desde el centro del Sol, [medido ortogonalmente hasta la órbita de la Luna] sobre ambos lados de la eclíptica, que es la posición límite en la que la Luna puede estar justamente en contacto aparente con el Sol.
Por ejemplo [ver Fig. 6.1] imaginemos AB como un arco de la eclíptica y GD como un arco del círculo inclinado de la Luna. Estos son sensiblemente paralelos uno con el otro, al menos tan lejos como conciernan las posiciones [de los cuerpos] en el momento de los eclipses.
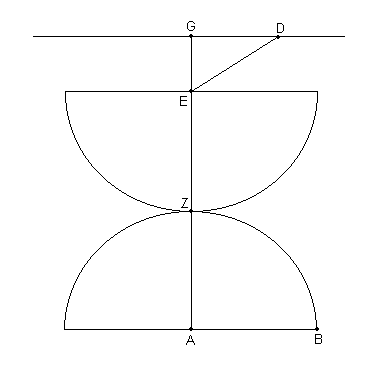
Dibujamos el arco AEG del gran círculo a través de los polos del círculo inclinado [de la Luna], e imaginar el semicírculo del Sol sobre el centro A, y el semicírculo aparente de la Luna sobre el centro E, en tal posición que este esté justamente tocando el Sol en el punto Z. Entonces el arco AE, que es la distancia de E, el centro aparente de la Luna, desde A, el centro del Sol, puede a veces ser tanto como de 0;33,20º, como lo [hemos] establecido anteriormente. Pero en las regiones extensas desde Meroe, donde el día más largo es de 13 horas equinocciales, por encima de las bocas del Borysthenes, donde el día más largo es de 16 horas equinocciales, el efecto máximo hacia el Norte de la Paralaje lunar para la Luna en su mínima distancia en las sizigias (si substraemos la paralaje solar) es de alrededor de 0;8º, y el efecto máximo hacia el Sur, bajo las mismas condiciones, es de 0;58º. Cuando su paralaje [latitudinal] es de 0;8º hacia el Norte, esta tiene una máxima paralaje longitudinal cerca de 0;30º, alrededor de Leo y de Gemini; y cuando su paralaje [latitudinal] es de 0;58º hacia el Sur, esta tiene una máxima paralaje longitudinal de alrededor de 0;15º, alrededor de Scorpius y de Pisces [9]. Entonces si suponemos que el centro verdadero de la Luna esta en D, y dibujar una línea DE, que representa la paralaje total, DG (representará) aproximadamente la paralaje en longitud, y GE la paralaje en latitud.
Por lo tanto, cuando la Luna esta al Norte del Sol y tiene una máxima paralaje hacia el Sur,
el arco DG será de 0;15º, y arco AEG [0;33,20° + 0;58° =] cerca de 1;31°.
Ahora la razón entre el arco desde el nodo G con el arco GA es de alrededor de (11 ½) / 1 para las distancias entre los límites de los eclipses: fácilmente esto puede ser visto desde nuestra previa demostración de la inclinación de la órbita lunar [10]. Entonces la distancia desde el nodo hasta G será de 17;26º, y GD sumada a esto da 17;41º.
Y cuando la Luna esta al Sur del Sol y tiene su máxima paralaje hacia el Norte, el arco DG será de 0;30º, y todo el arco AEG, [0;33,20º + 0;8º ≈] 0;41º. Por el mismo tipo de cálculo como el de antes, la distancia desde el nodo hasta G será de 7;52º, y la distancia total, incluyendo el arco GD, de 8,22º.
Por lo tanto, las posiciones límites, en las que la Luna puede estar justamente en contacto aparente con el Sol, para las regiones de nuestro mundo habitado anteriormente [mencionadas], ocurren cuando la distancia verdadera del centro de la Luna desde ambos de los nodos sobre su círculo inclinado esta a 17;41º hacia el Norte, o a 8;22º hacia el Sur.
Además, dado que, como demostramos, la Máxima Ecuación de la Anomalía es de 2;23º para el Sol y de 5;1º para la Luna cerca de las sizigias, a veces le será posible que la distancia verdadera de la Luna desde el Sol en las sizigias medias llegue a los 7;24º. Pero, en el tiempo en que la Luna le toma atravesar la distancia [de 7;24º], el Sol atravesará una distancia extra por alrededor de 1/13 ra. parte de esa cantidad, por ej. 0;34º; y nuevamente, mientras la Luna esta atravesando aquellos 0;34º extras, el Sol atravesará 1/13 ra. parte extra de esta [última cantidad], o cerca de 0;3º (una 1/13 ra. parte de este último [valor] es insignificante). Entonces si adicionamos la suma, 0;37º (que es 12 avas. partes del original 7;24º) [11] a los 2;23º de la [ecuación de la] anomalía solar, tomamos 3º, que es, aproximadamente, la máxima diferencia en longitud y [el argumento] en latitud entre la posición media [de los cuerpos] en la sizigia media y su posición verdadera [en la sizigia verdadera]. Entonces las posiciones límites en las cuales la Luna puede estar justamente en contacto aparente con el Sol, en las regiones arriba [mencionadas], ocurren cuando la distancia media del centro de la Luna desde ambos nodos sobre su circulo inclinado esta a 20;41º hacia el Norte, o 11;22º hacia el Sur. Y por el mismo argumento, el efecto anterior puede tomar lugar en las regiones en cuestión solo cuando la cantidad de la distancia de la Luna desde el límite Norte correspondiente (a la quinta columna de la (Tabla del Libro VI Capítulo 3) hasta la sizigia media, cae entre los 69;19º y los 101;22º, o entre los 258;38º y los 290;41º.
Seguidamente, para obtener los Límites Eclípticos de la Luna: tal como demostramos [más arriba], el radio de la Luna en su mínima distancia [en la sizigia] subtiende 0;17,40º, y el radio de la sombra, siendo alrededor de 2 ⅗ veces aquel [valor], llega a los 0;45,56º [12], esta claro que cuando la distancia verdadera del centro de la Luna es de 1;3,36º desde el centro de la sombra sobre ambos lados de la eclíptica (medido a lo largo del gran círculo dibujado a través de los polos de la órbita inclinada de la Luna), o es alrededor de 12;12º desde ambos nodos sobre su círculo inclinado (de acuerdo a la razón 1 / 11 ½), esa es la posición límite en la que la Luna justamente puede tocar la sombra. Y por el mismo argumento de la anomalía como fue deducido [más] arriba, la posición límite de la Luna para tocar la sombra ocurrirá cuando la distancia del centro medio de la Luna desde el nodo sobre su círculo inclinado sea de 15;12º. Por lo tanto la [posición media de la Luna], en la distancia desde el límite Norte, debe caer dentro de los límites [que van] desde los 74;48º hasta los 105;12º, o desde los 254;48º hasta los 285;12º.
Entonces, incluiremos en la precedente Tabla de las Sizigias estos números para [el argumento de] la latitud de la Luna en los Límites del Eclipse Solar y Lunar, con el propósito de proveer un método conveniente para determinar si [una sizigia dada] puede caer dentro de la categoría de un eclipse.
| Capítulo Anterior | Contenidos | Capítulo Siguiente |
| Libro VI |
| 01 | 02 | 03 |
| 04 | 05 | 06 |
| 07 | 08 | 09 |
| 10 | 11 | 12 |
| 13 |
Notas de referencia
- ↑ Ver HAMA 125-9, Pedersen 227-30.
- ↑ La palabra aquí utilizada, , significa "pronóstico [concerniente al clima]" o "significado del pronóstico" en HII 204, y HI 536,21; 537,8; 540,7. Es un significado tradicional (por ej. Ptolomeo en su Phaseis, Op. Min. 11,4:20,5), aplicando también al verbo (ibid. 31,10; cf. Apotelsmatica II 14, ed. Boll-Boer 100,17). Por lo tanto asumo este significado por donde este ocurra en el Almagesto, excepto en la frase , HI 188,3, donde significa meramente "nota de reconocimiento". Hay una buena discusión sobre y términos relacionados en Erwin Pfeiffer, Studien zum antiken Sternglauben 84-93.
- ↑ Leer seg. ' en cambio de seg. seg. (6;4º) en H477,10. La lectura esta confirmada por el cálculo ( ☉ = ♉︎ 16;13,25º) y por la posición verdadera de la Luna justamente más abajo. Los 6 ¼ se leen en los manuscritos A y D, en el Ar y probablemente en todos los manuscritos (por ej. el error es propio de Heiberg). Corregido por Manitius.
- ↑ Esto implica una ecuación de -1;33º, que esta muy bien de acuerdo con aquello derivado de una anomalía de 163;40º (abajo: un resultado preciso podría ser -1;32º), si uno utiliza la hipótesis lunar simple. No obstante, si uno calcula con una máxima precisión en las tablas Libro V Capítulo 9, uno encuentra ☽︎ = 216;23º (en una sizigia verdadera 2 seg. ≈ 5 ½º, que produce un cambio en de +50', y en consecuencia una disminución de 4' en la ecuación (precisamente la cantidad máxima por la cuál, de acuerdo con Ptolomeo al final del Libro V Capítulo 10, la hipótesis completa puede diferir de la simple en la sizigia). Esto también afecta a la posición de la Luna en su órbita, que debería ser de 8;22º (más bien que de 8;20º) desde el nodo.
- ↑ Oppolzer no. 1587: el eclipse medio [ocurrió] a las 23;44 hs. (≈ 01:45 hs. en Alejandría, estando más cerca del tiempo de la conjunción verdadera que uno encuentra en las tablas de Ptolomeo), magnitud de 7,4 dígitos.
Fecha y horas calculadas con un programa de computación desde la observación realizada por los griegos, quizás por maestros de Hiparco.
En ese tiempo el director de la biblioteca de Alejandría fue Apolonio Eidógrafo:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 1 de Mayo de 174 a. C. (-174) Parcial 00:09:47 hs. 01:28:12 hs. 02:46:37 hs. ------ 02:36:49 hs. 60,71 % - 0,6148 - 7,37 dígitos Scorpius 
Almagesto Observación 01.05.174 a. C. Nota del traductor al español: el cálculo de los dígitos es la fracción sombreada o eclipsada del diámetro lunar siendo igual a la Magnitud actual -menor o igual a 1- multiplicada por 12 dígitos (100% eclipsada). La carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Nuevamente (cf. más arriba en nota de referencia nro. 4) la ecuación implicada, [es de] -0;8º, suficientemente bien de acuerdo con aquella derivada de la anomalía de 178;46º coincidente con la hipótesis simple, pero la aplicación de la hipótesis completa produce una diferencia significante en la longitud verdadera de la Luna (♌︎ 5;13º) y su posición sobre la órbita (de 10;42º desde el nodo en cambio de 10;36º).
- ↑ Este eclipse fue observado por Hiparco, como uno podría esperar según la fecha y el lugar, confirmado casi al final del Libro VI Capítulo 9. En Pedersen no. 1638: tiempo 20;1 hs. (≈ 22:00 hs. en Alejandría), magnitud 3,2 dígitos, duración media: 58 minutos. Ptolomeo asume 30 minutos, que esta solamente cerca de la mitad de lo que él podría derivar desde sus propias tablas de eclipses, Libro VI Capítulo 8. Las dificultades asociadas con la observación y la reducción de este eclipse ha sido muy discutido: ver Fotheringham [3] 579, con referencias a una literatura más antigua, y a Britton [I] 94.
Fecha y horas calculadas con un programa de computación desde la observación realizada por Hiparco en la actual Rodas del siguiente:Eclipse lunar Fecha Tipo Eclipse 1° Contacto con la Umbra Eclipse Medio Último Contacto con la Umbra Duración de la Totalidad Tiempo Total del Eclipse % Oscurecimiento - Magnitud - Dígitos Luna en Carta 27 de Enero de 141 a. C. (-141) Parcial 20:52:14 hs. 21:45:11 hs. 22:38:08 hs. ------ 01:45:54 hs. 17,75 % - 0,2541 - 3,04 dígitos Leo 
Almagesto Observación 27.01.141 a. C. Nota del traductor al español: carta y datos elaborados con mi software de aplicación "M1 Sistema Astronómico"©.
- ↑ Ver HAMA 105-8, y cf. Libro V Capítulo 14 nota de referencia nro. 12 para los subsiguientes cálculos.
- ↑ Ptolomeo calcula el máximo efecto de la paralaje en los límites de la eclíptica para la región que abarca la "Clímata 7" standard (ver. Introducción "(ii) Astronomía Esférica"). Aquí hay algunos serios problemas en sus declaraciones (sin fundamentos), para ello ver HAMA 127-9.
- ↑ Por ej. tomando la inclinación de 5º (Libro V al final del capítulo 12), y tomando el pequeño triángulo esférico formado por la latitud, la eclíptica y la órbita de la Luna como plano, calculamos / = Cuerda 110° / Cuerda 10° = 119;32,37 / 10;27,32 = 11,43 / 1 ≈ (11 ½) / 1.
- ↑ Cf. Libro VI Capítulo 4 nota de referencia nro. 4.
- ↑ Notar que Ptolomeo toma precisamente 2 ⅗ veces el radio de la Luna, en cambio del valor 0;46º que actualmente ha derivado desde las observaciones.
