La teoría de la relatividad de Einstein/VII

VII

LA TEORIA GENERAL DE LA RELATIVIDAD DE EINSTEIN.

1.Relatividad en movimientos cualesquiera.

Al explicar la mecánica clásica hemos hablado detenidamente de los motivos que tuyo Newton para establecer los conceptos del espacio absoluto y del tiempo absoluto; pero al mismo tiempo hemos subrayado las objeciones que pueden hacerse a esas conceptuaciones desde el punto de vista de la crítica del conocimiento.

Newton apoya la hipótesis del espacio absoluto sobre la existencia de resistencias de inercia y fuerzas centrífugas. Estas no pueden evidentemente provenir de acciones recíprocas de los cuerpos, porque hasta donde alcanza la observación se manifiestan de igual manera en el universo total, independientemente de la distribución local de las masas. Por lo cual Newton infiere que dependen de las aceleraciones absolutas. De esta suerte se emplea el espacio absoluto como causa ficticia de fenómenos físicos.

Por el ejemplo siguiente se verá cuán poco satisfactoria es esta teoría.

En el espacio cósmico supongamos dos cuerpos fluidos S₁ y S₂ de igual substancia y magnitud, a tal distancia uno de otro que las acciones corrientes de gravitación de uno de ellos sean imperceptibles en el otro (fig. 124); cada uno de los cuerpos estará en equilibrio bajo la acción de la gravitación de sus partes unas sobre otras y de las demás fuerzas físicas, de suerte que sus partes no verifiquen movimientos relativos unas con respecto a otras. Pero los dos cuerpos realizan un movimiento relativo de rotación, con velocidad de rotación constante, al rededor de la línea que une sus centros; esto significa que un observador, en uno de los cuerpos S₁ aprecia una rotación uniforme del otro cuerpo S₂, con respecto a su propio punto de vista en reposo, y recíprocamente. Cada uno de los cuerpos es medido por observadores, que relativamente a él están en reposo; resultará que S₁ es una esfera y S₂ un elipsoide de revolución aplastado.

fig124

La mecánica de Newton sacaría del distinto comportamiento de los dos cuerpos la conclusión de que S₁ está inmóvil en el espacio absoluto y que S₂ verifica una rotación absoluta; las fuerzas centrífugas son las que causan el aplastamiento de S₂.

Por este ejemplo se ve claramente que el espacio absoluto entra en la mecánica de Newton como causa (ficticia), pues S₁ no puede ser causante del aplastamiento de S₂, puesto que ambos cuerpos están relativamente uno a otro en las mismas condiciones y, por tanto, no pueden deformarse uno a otro por distinta manera.

Pero el espacio, considerado como causa, no satisface la exigencia de la causalidad. Pues no conocemos ninguna otra manifestación de su existencia que las fuerzas centrífugas; no es, pues, posible justificar la hipótesis del espacio absoluto sino por los hechos mismos para cuya explicación se establece. Una sana crítica del conocimiento rechaza tales hipótesis construidas ad hoc; son harto fáciles y rompen todas las barreras que una investigación concienzuda tiende a levantar entre sus propios resultados y los engendros de la fantasía. Si la hoja de papel sobre la cual escribo se echase a volar de pronto, seria yo libre de formular la hipótesis de que el espíritu de Newton, fallecido hace siglos, ha venido a llevársela; pero como soy hombre razonable, no formulo tal hipótesis y pienso solamente en que la ventana está abierta, que mi mujer ha entrado en mi despacho y que se ha establecido una corriente de aire. Y aunque yo mismo no haya sentido la corriente, mi hipótesis no deja por ello de ser razonable, porque refiere el proceso, que tengo que explicar, a otro proceso observable. Esta selección crítica de las causas admisibles distingue la concepción racional, causal, del universo—a la cual desea pertenecer la investigación física—de toda otra concepción mística, espiritista y demás manifestaciones de la fantasía desbocada.

El espacio absoluto tiene, empero, un carácter realmente espiritista. A la pregunta: «¿Cuál es la causa de las fuerzas centrifugas?», se contesta: «El espacio absoluto.» Pero si se pregunta: «¿Qué es el espacio absoluto y en qué se manifiesta?», no da nadie otra contestación que la de decir: «El espacio absoluto es la causa de las fuerzas centrífugas; no tiene ninguna otra propiedad.» Esta contraposición demuestra bien que el espacio, considerado como causa de procesos físicos, debe excluirse de la imagen del universo.

No estará de más observar que las referencias a fenómenos electromagnéticos no altera en nada este juicio del espacio absoluto. En esos fenómenos aparecen, en sistemas de coordenadas en rotación, efectos y acciones análogos a las fuerzas centrífugas de la mecánica; pero éstos no son naturalmente nuevos e independientes argumentos que puedan militar en favor de la existencia del espacio absoluto, pues ya sabemos que, por medio de la ley de la inercia de la energía, la mecánica y la electrodinámica se han reunido en una unidad. Pero para nosotros es más cómodo operar solamente con los conceptos de la mecánica.

Volvamos ahora a los dos cuerpos S₁ y S₂; si el espacio no debe considerarse como causa de su distinto comportamiento, hemos de buscar otras causas reales.

Si admitimos que, fuera de los cuerpos S₁ y S₂, no existe ningún otro cuerpo material, entonces no es posible, en efecto, explicar el distinto comportamiento de S₁ y S₂. Pero tal comportamiento ¿es un hecho empírico? No lo es, sin duda alguna. No se pueden en ningún caso recoger experiencias sobre dos cuerpos aislados en el espacio cósmico. Admitir que dos cuerpos reales S₁ y S₂ se comportan diferentemente en esas circunstancias es cosa que no se funda en nada. Hay que aspirar, más bien, a que una mecánica satisfactoria excluya tal suposición.

Pero si en dos cuerpos reales S₁ y S₂ observamos el descrito comportamiento diferente—y conocemos, en efecto, planetas más o menos aplastados—no podremos considerar como causa de ello sino masas lejanas. En el mundo real existen, efectivamente, esas masas lejanas, el ejército de los astros todos. Sea cual fuere el cuerpo celeste que elijamos, siempre le veremos rodeado de otros muchos que se hallan separados de él por enormes distancias y que se mueven relativamente unos a otros con lentitud tal que pueden considerarse como una masa firme hueca, en cuya oquedad reside el referido cuerpo.

Esas masas lejanas tienen que ser la causa de las fuerzas centrífugas. Todas las experiencias convienen con este aserto; pues el sistema de referencia de la astronomía, con respecto al cual se determinan las rotaciones de los cuerpos celestes, está elegido de tal manera, que los movimientos aparentes de las estrellas fijas, relativamente al sistema de referencia, son muy desordenados y carecen de una dirección privilegiada. El aplastamiento de un planeta es tanto mayor cuanto mayor sea su velocidad de rotación respecto de ese sistema de referencia fijo en las masas lejanas.

Por consiguiente, exigiremos que las leyes de la mecánica y las de la física en general no contengan mas que las posiciones relativas y los movimientos relativos de los cuerpos. No debe haber a priori un sistema privilegiado, como lo son los sistemas inerciales de la mecánica de Newton y de la teoría especial de la relatividad de Einstein, pues de otra suerte entrarían en las leyes naturales las aceleraciones absolutas con respecto a ese sistema de referencia privilegiado y no sólo los movimientos relativos de los cuerpos.

Llegamos así al postulado de que las verdaderas leyes de la física deben valer por igual manera para sistemas de referencia que se hallen en un movimiento cualquiera. Y esta es una considerable ampliación del principio de relatividad.

2. El principio de equivalencia.

El cumplimiento de ese postulado requiere una fórmula completamente nueva de la ley de inercia, pues ésta es el fundamento de la situación especial en que se colocan los sistemas inerciales. La inercia de un cuerpo no debe ya considerarse como efecto del espacio absoluto, sino de los demás cuerpos.

Ahora bien; sólo una acción recíproca conocemos entre todos los cuerpos materiales, y es ésta la gravitación; sabemos, ademas, que la experiencia nos ha ofrecido una notable conexión entre gravitación e inercia, la ley de la igualdad de la masa pesada y de la masa inerte (II, 12, pág. 52). Los dos fenómenos de la inercia y de la atracción, tan distintos en la fórmula de Newton, tendrán, pues, una raíz común.

Este es el gran descubrimiento de Einstein, por el cual el principio general de la relatividad ha dejado de ser un postulado de la critica del conocimiento para transformarse en una ley de las ciencias exactas.

Podemos caracterizar el objetivo de la investigación siguiente de este modo: en la mecánica corriente, el movimiento de un cuerpo pesado—sobre el cual no actúen fuerzas electromagnéticas u otras cualesquiera—queda definido por dos causas: 1.ª, su inercia en aceleraciones respecto del espacio absoluto; 2.ª, la gravitación de las restantes masas. Ahora hay que buscar una fórmula de la ley del movimiento en la cual la inercia y la gravitación se fundan en un concepto superior, de tal suerte que el movimiento esté determinado sólo por la distribución de las restantes masas en el mundo. Hasta llegar al establecimiento de la nueva ley, hemos de recorrer, empero, un largo camino y vencer algunas dificultades de concepto.

Ya hemos explicado antes detenidamente la ley de la igualdad entre la masa inerte y la masa pesada. Para los procesos terrestres dice esta ley: todos los cuerpos caen con igual rapidez; para los movimientos de los astros expresa que la aceleración es independiente de la masa del cuerpo en movimiento. También hemos dicho que esta ley ha sido experimentalmente comprobada por Eötvös con muy exactas mediciones, pero que, sin embargo, en la mecánica clásica no figura entre las leyes fundamentales, sino que es considerada casi como un obsequio casual de la naturaleza.

Ahora todo esto varía; la ley colócase en la cúspide, no sólo de la mecánica, sino de toda la física.

Debemos, pues, aclararla hasta que se vea bien su contenido fundamental. Aconsejamos al lector que haga el sencillo experimento siguiente: Tome dos cuerpos ligeros, pero de distinto peso, por ejemplo, una moneda y un pedazo de goma de borrar; colóquelos sobre la palma de su mano. Sentirá el peso de los dos cuerpos como presión sobre la mano y esta presión será diferente. Mueva luego la mano rápidamente hacia abajo; sentirá una disminución de la presión de los dos cuerpos. Si se repite cada vez con más rapidez el movimiento, llegará un momento en que los cuerpos se separen de la mano y se queden atrás durante el movimiento; ello sucederá evidentemente tan pronto como la mano, en su movimiento, sea más veloz que la caída de los dos cuerpos. Pero como estos dos, a pesar de su diferente peso, caen con igual rapidez, resulta que, al separarse de la mano, permanecen ambos a la misma altura, uno junto a otro.

Imaginemos ahora unos enanillos que vivan sobre la mano y no sepan nada del mundo exterior. ¿Cómo interpretarán el proceso? Es fácil introducirse en el alma de esos observadores, que efectúan el mismo movimiento, mientras se hace el experimento y se atiende a las varias presiones y movimientos de los cuerpos respecto de la mano. Estando la mano en reposo, los enanillos podrán comprobar el peso diferente de los dos cuerpos. Ahora la mano desciende y los enanillos observan una diminución en el peso de los cuerpos; buscarán la causa de ello y notarán que su residencia, la mano, desciende relativamente a los cuerpos circundantes, las paredes de la habitación. Pero podemos encerrar los enanillos, con los dos cuerpos de ensayo, en un cajón cerrado y mover éste hacia abajo con la mano. Entonces los observadores, dentro del cajón no verán nada que les permita conocer el movimiento del cajón. Sólo podrán comprobar el hecho de que el peso de todos los cuerpos en el cajón disminuye por igual. Si la mano mueve el cajón con rapidez tal que los objetos dentro de él se quedan atrás, los observadores en el cajón verán admiradísimos que esos objetos, de peso bastante notable, vuelan hacia arriba; adquieren un peso negativo o, mejor dicho, la fuerza de la gravedad no actúa ya hacia abajo, sino hacia arriba. Y los dos cuerpos, a pesar de su diferente peso, ascienden con igual rapidez. Los enanillos del cajón pueden explicar estas observaciones de dos maneras: o bien piensan que el campo de gravedad permanece inalterado, pero que el cajón recibe una aceleración en la dirección del campo, o admiten que las masas atractivas en el suelo del cajón han desaparecido y, en cambio, han aparecido otras en el techo, cambiando así la dirección de la gravedad. Nosotros preguntamos ahora: ¿Hay algún medio para decidir entre ambas posibilidades, haciendo experimentos dentro del cajón?

Debemos contestar que la física no conoce medio alguno. Efectivamente, la acción de la gravedad no se distingue en nada de la acción de la aceleración; ambas son enteramente equivalentes. Ello obedece esencialmente a que todos los cuerpos caen con igual rapidez; si no fuese así, podría distinguirse al punto si un movimiento acelerado de cuerpos con diferente peso es producido por la atracción de masas extrañas, o sólo es la resultante aparente de una aceleración de la residencia del observador. Pues en el primer caso los cuerpos de diferente peso moveríanse con diferente rapidez, y en el segundo la aceleración de todos los cuerpos libremente movibles con respecto al observador sería igual en todos y, a pesar del distinto peso, caerían todos con igual rapidez.

Este principio de la equivalencia, establecido por Einstein, pertenece, pues, al número de los que en este libro ocupan un lugar preferente, esto es, a los que afirman la imposibilidad de establecer una afirmación física, la imposibilidad de distinguir entre dos conceptos; la física rechaza tales conceptos y tales afirmaciones, pues sólo poseen realidad física los hechos comprobables.

La mecánica clásica dintingue entre el movimiento de un cuerpo abandonado a si mismo, no sometido a fuerza alguna, movimiento de inercia y el movimiento de un cuerpo bajo la acción de la gravitación. El primero es rectilíneo y uniforme en un sistema inercial; el segundo verifícase en trayectorias curvas y no uniformemente. Según el principio de equivalencia debemos prescindir de esa distinción, pues con sólo trasladarse a un sistema de referencia acelerado puede transformarse el movimiento de inercia rectilíneo y uniforme en un movimiento curvilíneo acelerado, el cual ya no es discernible de un movimiento producido por gravitación; y la inversa es válida también, por lo menos para trozos limitados del movimiento, como luego explicaremos en detalle. A partir de ahora, llamaremos movimiento de inercia a todo movimiento de un cuerpo sobre el cual no actúe ninguna fuerza eléctrica o magnética, o de cualquier otro origen y que se halle sólo bajo la influencia de masas gravitantes; las palabras movimiento de inercia tienen, pues, ahora una significación más general que antes. La ley que dice que el movimiento de inercia es rectilíneo y uniforme relativamente a un sistema inercial, la ley corriente de la inercia, cesa, pues, de ser válida. Y nuestro problema es justamente el de formular la ley del movimiento de inercia en el sentido generalizado.

La solución de este problema nos libra del espacio absoluto y proporciona una teoría de la gravitación que se halla en más profunda relación con los principios de la mecánica que en la teoría de Newton.

Vamos a completar estas explicaciones en el aspecto cuantitativo. Ya hemos demostrado (III, 8, pág. 92) que las ecuaciones del movimiento, en la mecánica, referidas a un sistema S que tiene la aceleración constante k con respecto a los sistemas inerciales, pueden escribirse en la forma:

$mb=K'$,

significando K' la suma de la fuerza real K y de la fuerza de inercia -mk:

$K'=K-mk$

Ahora bien; si la fuerza K es la gravedad, tendremos K = mg, y, por tanto,

$K'=m(g-k)$.

Eligiendo convenientemente la aceleración k del sistema de referencia S, puede darse a la diferencia g - k un valor cualquiera positivo o negativo, y también hacerla igual a cero. Si, por analogía con la electrodinámica, se llama a la fuerza por la unidad de masa campo de fuerza de la gravedad, y al espacio donde ésta actúa campo de gravedad, puede decirse: eligiendo convenientemente el sistema de referencia acelerado puede crearse un campo de gravedad constante, puede debilitarse, aniquilarse, fortificarse, invertirse, un campo de gravedad actual.

Todo campo de gravedad puede considerarse como aproximadamente constante dentro de una parte suficientemente pequeña de espacio y durante un tiempo corto; por lo cual es siempre posible hallar un sistema de referencia acelerado con relación al cual no haya ningún campo de gravedad en la esfera limitada del tiempo y del espacio.

Se preguntará ahora si, por simple elección del sistema de referencia, no sería posible suprimir todo campo gravitatorio en su extensión total y para todo tiempo; es decir, si, en cierto modo, no podría concebirse toda gravitación como «aparente». Pero tal no es el caso, evidentemente. El campo de la esfera terrestre, por ejemplo, no puede suprimirse por completo, pues está dirigido hacia el centro y la aceleración debería, por tanto, partir del centro; pero esto no es posible. Y aunque se admitiese—y tendremos que hacerlo—que el sistema de referencia no fuese rígido, sino que se extendiera aceleradamente alrededor del centro de la tierra, aun este movimiento no seria posible sino por tiempo limitado; el centro le pondría límite. Haciendo girar alrededor de un eje el sistema de referencia, obtiénese una fuerza de inercia, dirigida en dirección que se aleja del eje (III, 9, pág. 97, fórmula [27]), y que es la fuerza centrífuga

$mk={\frac {1\pi ^{2}r}{T^{2}}}$

Esta compensa el campo de gravedad de la tierra sólo en cierta distancia r, a saber: el radio de la trayectoria lunar, pensada como un círculo, con el tiempo T de revolución.

Existen, pues, campos gravitatorios «verdaderos»; pero el sentido de esta palabra es distinto en la teoría general de la relatividad que en la mecánica clásica, pues eligiendo convenientemente el sistema de referencia es siempre posible suprimir una parte cualquiera, suficientemente pequeña, del campo. Más tarde estableceremos con más exactitud el concepto de campo gravitatorio.

Naturalmente, hay ciertos campos gravitatorios que pueden ser suprimidos en toda su extensión por medio de una elección conveniente del sistema de referencia. Para encontrarlos, basta partir de un sistema de referencia en el cual una parte del espacio no tenga campo e introducir un sistema de referencia acelerado de un modo cualquiera; entonces, con relación a éste, existe un campo gravitatorio. Este desaparece tan pronto como volvemos al primitivo sistema de referencia. El campo centrífugo

$k={\frac {4\pi ^{2}r}{T^{2}}}$

es de esta especie. La cuestión de cuándo un campo gravitatorio pueda desaparecer en toda su extensión, por elección del sistema de referencia, no puede ser contestada, como es natural, sino por la teoría ya completa y terminada.

3. La geometría euclidiana es inaplicable.

Pero antes de proseguir, debemos vencer una dificultad que exige considerables esfuerzos.

Estamos acostumbrados a representar los movimientos como líneas universales en el universo de Minkowski. El andamiaje de esta geometría cuatridimensional fué dado por las lineas universales de los rayos luminosos y las trayectorias de las masas inertes, movidas sin que sobre ellas actúen fuerzas; estas líneas universales son en la antigua teoría unas lineas rectas relativamente a los sistemas inerciales. Pero si se da validez a la relatividad general, resultan entonces los sistemas acelerados igualmente válidos, y en éstos las líneas universales, que antes eran rectas, son ahora curvas (III, 1, pág. 68, figura 31). En cambio, otras líneas universales se hacen rectas. Por lo demás, esto rige también para las trayectorias de espacio. Los conceptos de recta y curva son relativizados, en cuanto que son referidos a las trayectorias de los rayos luminosos y de los cuerpos libremente móviles.

De esta suerte tambaléase todo el edificio de la geometría euclidiana del espacio cósmico. Pues ésta descansa esencialmente (véase III, 1, pág. 67) en la ley clásica de la inercia que establece las líneas rectas.

Podría pensarse que esta dificultad es obviable empleando solamente medidas rígidas para la definición de los elementos geométricos, tales como recta, plano, etc.. Pero tampoco es esto posible, como demuestra Einstein, de la siguiente manera:

Partimos de un espacio en el cual, durante cierto tiempo, no existe ningún campo gravitatorio relativamente a un sistema de referencia S₁, convenientemente elegido.

Luego consideramos un cuerpo que gira en ese espacio con la velocidad angular constante, por ejemplo, un disco circular plano y perpendicular al eje de rotación (fig. 125); introducimos un sistema de referencia S' fijo en ese disco. En S' domina, pues, un campo gravita torio dirigido hacia afuera dado por la aceleración centrifuga

$k={\frac {4\pi ^{2}r}{T^{2}}}$

fig125

Ahora un observador situado en S' quiere medir el disco circular. Para ello usa como unidad una vara de determinada longitud, la cual debe estar en reposo con relación a S'. Otro observador situado en el sistema de referencia S usa como unidad la misma vara, la cual en este caso debe hallarse en reposo relativamente a S.

Habremos de admitir que los resultados del principio especial de relatividad permanecen exactos, en cuanto que nos limitemos a partes de espacio y a tiempos en los cuales el movimiento pueda considerarse como uniforme. Para que ello sea posible, supongamos que la vara unidad es pequeña comparada con el radio del disco.

Si el observador situado en S' coloca la vara en la dirección del radio del disco, el observador situado en S establecerá que la longitud de la vara en movimiento relativamente a S permanece igual a 1, pues el movimiento de la vara es perpendicular a su dirección longitudinal. Pero si el observador en S' coloca la vara en la periferia del disco, ésta parecerá más corta al observador situado en S, según la teoría especial de la relatividad. Si admitimos que hacen falta 100 varas para cubrir el diámetro del disco, necesitará el observador situado en S π veces 100, esto es, 3,14... × 100, o sean 314 varas para medir la circunferencia del disco, mientras que el observador situado en S' no podrá con ese mismo número de varas medir esa misma circunferencia; pues las varas inmóviles en S' aparecen, desde S, más cortas, y el número de 314 no basta para abarcar toda la periferia del disco.

Según esto, el observador situado en S' afirmaría que la relación de la circunferencia al diámetro no es π = 3,14..., sino mayor. Esto, empero, contradice a la geometría de Euclides.

Otro tanto sucede en la medición de los tiempos. Si ponemos dos relojes iguales, uno en el centro y el otro en la periferia del disco, en reposo relativamente a éste, el último, juzgado desde el sistema S, andará más despacio que el primero, porque está en movimiento con relación a S.

Un observador situado en el centro del disco comprobaría, evidentemente, lo mismo. Es, pues, imposible llegar a una definición racional del tiempo, por medio de relojes en reposo relativamente al sistema de referencia, si este sistema gira, se halla en movimiento acelerado, o, lo que, según el principio de equivalencia, es lo mismo, si existe en él un campo gravitatorio.

En el campo gravitatorio una vara es más o menos corta, un reloj anda más o menos despacio, según el sitio en que se encuentre el instrumento de medida.

Esto descompone por completo el fundamento del universo espacio-tiempo, sobre el cual descansaban todas nuestras reflexiones. Nos vemos precisados, una vez más, a generalizar los conceptos de espacio y tiempo; pero esta vez por tan radical manera que excede con mucho en importancia a todas las anteriores.

Es evidentemente absurdo definir las coordenadas y el tiempo x, y, z, t, del modo corriente y habitual, pues al hacerlo así considéranse como dados absolutamente los conceptos fundamentales de la geometría: recta, plano, círculo, etc... y se supone la validez de la geometría euclidiana en el espacio y, respectivamente, de la generalización de Minkowski en el universo espacio-tiempo.

Plantéase, pues, el problema de representar el universo cuatridimensional y sus leyes sin partir a priori de una geometría determinada.

Parece que ahora se abre el suelo bajo nuestras plantas; todo vacila; la curva es recta, la recta es curva. Pero la dificultad de la empresa no logró intimidar a Einstein}. La matemática había realizado importantes trabajos anteriores que abrían el camino a las nuevas concepciones; Gauss (1827) había bosquejado la teoría de las superficies curvas en la forma de una geometría general de dos dimensiones, y Riemann (1854) había fundado la teoría del espacio como continuo de múltiples dimensiones. No podemos hacer uso aquí de estos auxilios matemáticos; sin ellos, empero, no es posible entender profundamente la teoría general de la relatividad. No espere, pues, el lector que las siguientes explicaciones le den una noción completa de las teorías de Einstein; encontrará imágenes y analogías, que son siempre malos sustitutos de los conceptos exactos. Pero si mis insinuaciones le sirven de acicate para emprender estudios más profundos, habré cumplido mi objeto.

4. La geometría en superficies curvas.

El problema de constituir una geometría sin el andamiaje a priori de las líneas rectas y sus leyes euclidianas de relación no es empresa tan desacostumbrada como a primera vista parece. Imaginemos que un agrimensor tiene que medir un terreno ondulado, cubierto de espeso bosque, y establecer el mapa del mismo. Desde cualquier punto del terreno no puede abarcar mas que un contorno limitadísimo; los instrumentos para tender visuales (teodolitos) de poco le sirven; en lo esencial hállase atenido a la cinta métrica. Con ésta puede medir pequeños triángulos, cuadriláteros, cuyos vértices señalará con estacas, y añadiendo unas a otras esas figuras directamente mensurables irá progresando poco a poco por las partes más remotas del terreno que no son inmediatamente visibles.

Dicho abstractamente: el agrimensor puede aplicar los métodos de la geometría euclidiana a pequeñas porciones del terreno. Pero el conjunto del territorio no es accesible a esta geometría, y sólo paso a paso, progresando de un lugar a otro, puede llegar a estudiarse geométricamente. Pero hay más aún: la geometría euclidiana no es válida estrictamente en un terreno ondulado; no hay en él, en general, líneas rectas. Pequeños trozos de la longitud de la cinta métrica podrán considerarse como rectas; pero por valles y montes no hay recta que atraviese, si quiere ir pegada al suelo. La geometría euclidiana sirve, pues, en lo pequeño, en la esfera de lo infinitesimal; pero en lo grande rige una teoría más general del espacio o, mejor dicho, de las superficies.

Si el agrimensor quiere proceder sistemáticamente, empezará por cubrir el terreno de una red de lineas, que indicará con estacas o por medio de árboles señalados; necesitará dos grupos de líneas que se crucen (fig. 126). Las líneas serán lo más posible de curvatura regular y estarán numeradas sucesivamente en cada grupo; se emplea como signo para los números de un grupo la letra x, y para los del otro grupo, la letra y.

fig126

Cada intersección tiene, pues, dos números x, y; por ejemplo: x = 3, y = 5. Los puntos intermedios se caracterizan por medio de quebrados de x y de y.

Este método para determinar los puntos de una superficie ondulada lo empleó por primera vez Gauss; por eso se llaman coordenadas de Gauss estas x é y.

Lo esencial aquí es que los números x é y no significan longitudes, ni ángulos, ni otras magnitudes mensurables, sino nada más que números; ni más ni menos que el sistema americano de numerar calles y casas.

Compete al agrimensor introducir la medida en esa numeración de los puntos del terreno. Su cinta métrica alcanzará, por ejemplo, la extensión de una malla en la red de las coordenadas de Gauss.

El agrimensor empezará luego a medir malla por malla; cada una de éstas puede considerarse como un pequeño paralelogramo y queda determinada por dos longitudes y un ángulo. El agrimensor tiene que medirlos y apuntarlos en el mapa en cada malla. Una vez realizado este trabajo, domina la geometría del terreno completamente merced a su mapa.

En lugar de los tres datos por cada malla— dos lados y un ángulo—suele emplearse otro método que tiene la ventaja de una mayor simetría.

fig127

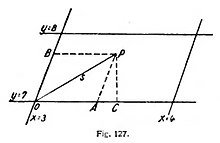
Consideremos una malla, un paralelogramo, cuyos lados corresponden a dos números enteros consecutivos—por ejemplo: x = 3, x = 4 é y = 7, y = 8 (fig. 127)—. Sea P un punto cualquiera en el interior; su distancia al vértice O, señalado con el número más pequeño, es s. Esta distancia se mide con la cinta métrica. Por P tracemos las paralelas a las líneas de la red, que encontrarán a éstas en A y B. Sea, además, C el pie de la perpendicular bajada de P a la línea coordenada x.

Los puntos A y B tienen también números o coordenadas de Gauss en la red; se determina A, por ejemplo, midiendo el lado del paralelogramo en que está A y la distancia AO, y entonces la relación de ambas longitudes se tomará como aumento de la coordenada x de A con respecto a O. Señalaremos este aumento mismo con la letra x, eligiendo O como punto cero de las coordenadas de Gauss. De igual manera determinamos la coordenada gaussiana y, de B, como la relación en que B divide al correspondiente lado del paralelogramo. Entonces x é y son, evidentemente, las coordenadas gaussianas del punto P.

Pero la verdadera longitud de OA no es x, naturalmente, sino, por ejemplo, ax, donde a es un número determinado que la medición nos proporcionará; de igual manera la verdadera longitud de OB no es y, sino by. Si el punto P se mueve, varían sus coordenadas gaussianas; pero los números a y b, que indican la relación de las coordenadas gaussianas con las longitudes verdaderas, permanecen inalterados.

Expresemos ahora la distancia OP = s merced al triángulo rectángulo OPC, según el teorema de Pitágoras:

$s^{2}=OP^{2}=OC^{2}+CP^{2}$.

Pero

$OC=OA+AC$;

luego

$s^{2}=OA^{2}+2OA\cdot AC+AC^{2}+CP^{2}$

Pero, por otra parte, en el triángulo rectángulo APC tenemos:

$AC^{2}+CP^{2}=AP^{2}$;

por lo cual,

$s^{2}=OA^{2}+2OA\cdot AC+AP^{2}$.

Aquí es OA = ax, AP = by; además AC es la proyección de AP, por lo cual se halla en relación con él; como AP = by, podemos escribir que AC = cy. Obtenemos asi:

$s^{2}=a^{2}x^{2}+2acxy+b^{2}y^{2}$

Pero a, b y c son números fijos de relación; estos tres factores de esta ecuación suelen designarse de otro modo, a saber:

$s^{2}=g_{11}x^{2}+2g_{12}xy+g_{22}y^{2}$[87]

Esta ecuación puede llamarse el teorema de Pitágoras generalizado para coordenadas de Gauss.

Las tres magnitudes g₁₁, g₁₂ y g₂₂ pueden servir tan bien como los lados y el ángulo para determinar las relaciones efectivas de magnitud del paralelogramo. Por eso llevan el nombre de factores determinativos de las medidas. De malla en malla cambian sus valores, que son apuntados en el mapa o tienen que ser indicados como «funciones» por medio de la matemática analítica. Pero una vez conocidos para cada malla, puede calcularse por la fórmula [87] la verdadera distancia de un punto cualquiera P, dentro de una malla cualquiera, al punto cero de la malla, si están dados los números o coordenadas gaussianas x é y de P.

Los factores determinativos de las medidas representan, pues, toda la geometría en la superficie.

Se objetará a esta afirmación que no puede ser exacta, porque la red de coordenadas gaussianas ha sido elegida a capricho, y ese capricho trasládase a las g₁₁, g₁₂ y g₂₂. Es verdad; podría elegirse otra red y se encontraría, para la distancia de los mismos puntos OP, una expresión igualmente construida que la [87], aunque con otros factores g'₁₁, g'₁₂ y g'₂₂. Pero, naturalmente, existen reglas para inferir éstos por cálculo de los g₁₁, g₁₂ y g₂₂; existen fórmulas de transformación de índole semejante a las que ya hemos conocido.

Todo hecho real geométrico en la superficie debe poder expresarse por fórmulas tales que permanezcan inalteradas en cualquier cambio de las coordenadas gaussianas, esto es, que sean invariantes. La geometría de las superficies se transforma así en una teoría de las invariantes de índole muy general, pues las líneas de la red de coordenadas son enteramente caprichosas, con tal de que se elijan de curvatura constante y cubran la superficie simplemente y sin dejar huecos.

¿Cuáles son ahora los problemas geométricos que el agrimensor habrá de resolver tan pronto como se haya proporcionado la determinación de las medidas?

Sobre la superficie curva no hay líneas rectas, pero hay líneas que son las más rectas; son también aquellas que establecen el enlace más corto entre dos puntos. Su nombre científico es líneas geodésicas. Caracterízanse matemáticamente por lo siguiente: divídase una línea cualquiera sobre la superficie en pequeñas secciones mensurables de la longitud s₁, s₂, s₃....; entonces la suma

$s_{2}+s_{2}+s_{3}+\dots$

fig128

es para la linea geodésica entre dos puntos P₁ y P₂ más pequenña que para otra cualquier línea entre ellos (fig. 128). Las s₁, s₂.... pueden determinarse por puro cálculo merced al teorema de Pitágoras generalizado [87], si g₁₁, g₁₂ y g₂₂ son conocidas.

Sobre la superficie de una esfera es sabido que las lineas más cortas son los «circulos máximos»; éstos están formados por los planos secantes que pasan por el centro de la esfera. En otras superficies son muchas veces curvas muy complicadas; y, sin embargo, son las más sencillas las que forman el andamiaje de la geometría en las superficies, justamente como son las líneas rectas las que forman el andamiaje de la geometría euclidiana del plano.

Las líneas geodésicas son, naturalmente, expuestas por fórmulas invariantes; son reales propiedades geométricas de las superficies. De esas invariantes pueden deducirse todas las superiores, pero no podemos detenernos en este punto.

Otra propiedad fundamental de las superficies es su curvatura. Comúnmente defínese merced a la tercera dimensión del espacio; la curvatura de una esfera se mide, por ejemplo, por medio del radio de la esfera, es decir, de una distancia que se halla fuera de la superficie de la esfera. Nuestro agrimensor, en la floresta montañosa, no podrá emplear ese medio; no puede salir de su superficie, y debe probar a establecer las relaciones de curvatura con sólo su cinta métrica. Y ello es realmente posible; Gauss lo ha demostrado sistemáticamente. Podemos comprenderlo por la siguiente sencilla reflexión.

El agrimensor, con su cinta métrica, mide 12 cuerdas de igual longitud y forma con ellas el hexágono reproducido en la figura 129. Según un conocidísimo teorema de la geometría plana corriente, es, efectivamente, posible mantener las 12 cuerdas al mismo tiempo tensas en ese orden sobre el plano; ello es, en verdad, muy admirable, pues estando ya en tensión cinco de los seis triángulos equiláteros, tiene el sexto que acomodarse perfectamente al espacio restante. En la escuela se aprende que coincide muy bien el sexto triángulo, y lo que se aprende en la escuela no es cosa sobre la cual más tarde se reflexione mucho. Y, sin embargo, es bien extraño y admirable que una cuerda de la misma longitud que las otras llene exactamente el hueco que queda.

fig129

Y, en efecto, ello no sucede nada más que en el plano; si se ensaya en una superficie curva, de suerte que el centro y los seis vértices estén en ella, no se cierra el hexágono; en el lomo de las montañas y en el fondo de los valles resulta la última cuerda demasiado larga; en los desfiladeros—partes de la superficie curvadas en forma de silla de montar—resulta la última cuerda demasiado corta.

Aconsejamos al lector que haga la prueba con doce trozos de hilo en un cojín.

Así se obtiene, empero, un criterio para hallar la curvatura de las superficies sin salir de éstas. Si el hexágono se construye bien, la superficie es plana; si no, es curva. No nos meteremos en deducir la medida de la curvatura; esta indicación bastará para hacer plausible el que, en efecto, pueda definirse estrictamente. Es evidente que la curvatura está en conexión con las variaciones que los factores determinativos de las medidas experimentan de lugar en lugar; la medida de la curvatura puede expresarse, como Gauss ha demostrado, por medio de las g₁₁, g₁₂ y g₂₂, y es una invariante de la superficie.

La teoría de la superficie establecida por Gauss es un modo de hacer geometría que podría caracterizarse, usando una expresión física, como teoría de acción próxima. No son las leyes de las superficies en lo grande las que primariamente se dan, sino sus propiedades diferenciales, los coeficientes determinativos de las medidas y las invariantes, que con ellos se forman, sobre todo la medida de la curvatura; la figura de la superficie y sus propiedades geométricas en conjunto podrán luego establecerse por medio de cálculos que se parecen mucho a la solución de las ecuaciones diferenciales en la física. En cambio, la geometría de Euclides es una teoría típica de acción a distancia. Por eso la física actual, que está toda construida sobre los conceptos de la acción próxima del campo, no se compadece bien con el esquema de Euclides y, siguiendo el ejemplo de Gauss, debe emprender nuevos derroteros.

5. El continuo de dos dimensiones.

Imaginemos que nuestro agrimensor maniobra con su hexágono para determinar la curvatura del terreno; pero no advierte que un rayo de sol, colándose por la enramada, viene a herir el centro del hexágono, el punto donde se reúnen las cuerdas. Estas, bajo la acción del calor, se dilatan un poco, y resulta que las seis cuerdas radiales son algo más largas que las seis periféricas, por lo cual estas últimas no coinciden ya en sus extremidades. El agrimensor entonces, aunque el terreno en realidad sea plano, creerá encontrarse en una loma (o una depresión) muy poco pronunciada. Si es concienzudo, repetirá la medición con cuerdas de otro material; éstas se dilatarán por el calor más o menos que las anteriores, y así el agrimensor se dará cuenta del error y lo rectificará.

Pero supongamos que la variación de longitud producida en las cuerdas por el calor sea igual para todos los materiales disponibles. En tal caso, el error no será nunca advertido. Las llanuras pasarán por lomas y las lomas por llanuras. O supongamos también que ciertas fuerzas naturales, que aun desconocemos, influyan en la longitud de metros y cuerdas por igual en todas. La geometría que el agrimensor establece con cintas métricas y polígonos será muy distinta de la verdadera geometría de la superficie; pero mientras opere en la superficie, sin posibilidad de adoptar un punto de vista más elevado, de emplear la tercera dimensión, seguirá firmemente persuadido de haber establecido la geometría exacta de la superficie.

Estas reflexiones nos muestran que el concepto de la geometría en una superficie o, como dice Gauss, de la geometría intrínseca, no tiene nada que ver con la forma de la superficie tal como aparece a un observador que dispone de la tercera dimensión espacial. Una vez dada la unidad de longitud por una cinta métrica o una vara de medir, queda plenamente determinada la geometría en la superficie, relativamente a esa determinación de las medidas, aunque el metro en realidad sufra, durante la medición, cuantas alteraciones se quiera. Para un ser recluído en la superficie no existen tales alteraciones, en cuanto que todas las substancias las sufren por igual manera. Y ese ser establecerá curvaturas donde en realidad no las hay, y recíprocamente. Pero esta expresión: «en realidad», carecerá de sentido para seres superficiales que no tengan representación alguna de una tercera dimensión, como nosotros los hombres no tenemos representación alguna de una cuarta dimensión espacial.

Es, pues, para esos seres también absurdo designar su universo con el nombre de «superficie», el cual indica un concepto que reside en un espacio de tres dimensiones; mejor será decir que es un «continuo de dos dimensiones». Este tiene una geometría determinada; tiene determinadas líneas geodésicas—o sea las más cortas—; tiene una determinada «medida de curvatura» en cada sitio; pero aquellos seres puramente superficiales, que hemos imaginado, no unirán a estas palabras las mismas representaciones que nosotros unimos al concepto intuitivo de curvatura de una superficie, sino que mentarán con ellas exclusivamente el hecho de que el hexágono de cuerdas encaja más o menos, y esto es todo.

Si el lector consigue reproducir en su ánimo las sensaciones de ese ser superficial y representarse el universo tal como a éste le aparece, es que está ya maduro para seguir caminando por la vía de la abstracción.

En efecto; pudiera ser que nos sucediera otro tanto a nosotros, hombres, en nuestro universo de tres dimensiones. Quizá este universo tridimensional resida en un espacio cuatridimensional, como la superficie reside en nuestro espacio tridimensional; quizá haya algunas fuerzas, desconocidas para nosotros, que en algunas partes del espacio alteren las longitudes, sin poderlo nosotros apreciar nunca directamente. Pero entonces sería posible que en esas partes del espacio un poliedro, construido como el hexágono, no encajase bien, debiendo, sin embargo, encajar según las leyes de la geometría corriente.

¿Hemos observado alguna vez algo parecido? Desde la antigüedad, la geometría de Euclides ha sido siempre considerada como exacta; sus teoremas fueron incluso declarados exactos a priori y como santificados por la filosofía crítica de Kant (1781). Pero los grandes matemáticos y físicos, sobre todo Gauss, Riemann y Helmholtz, no han compartido nunca esa creencia universal. Gauss mismo verificó una vez cierta grandiosa medición, para comprobar un teorema de la geometría euclidiana, a saber: el que dice que la suma de los ángulos de un triángulo es igual a dos rectos (180 °). Midió el triángulo formado por tres montañas: Brocken, Hohe Hagen e Inselberg, y el resultado fué que la suma de los ángulos tiene el valor exacto, dentro de los límites del error.

Gauss fué muy criticado por los filósofos a causa de ese experimento. Dijéronle, sobre todo, que aun cuando hubiese encontrado variaciones, habría demostrado a lo sumo que los rayos luminosos entre los telescopios son desviados por algunas causas físicas, acaso desconocidas, pero nunca nada sobre la validez o invalidez de la geometría euclidiana.

Einstein sostiene ahora, como ya hemos dicho antes (página 339), que la geometría del mundo real es, efectivamente, no euclidiana, y apoya su aserto en ejemplos muy concretos.

Para comprender la relación en que se halla su teoría con las anteriores discusiones sobre los fundamentos de la geometría, debemos hacer algunas consideraciones de principios, las cuales tocan bastante a la filosofía.

6. Matemática y realidad.

Se trata del objeto de los conceptos geométricos en general. El origen de la geometría es seguramente el arte práctico del agrimensor, esto es, una teoría puramente empírica. Los antiguos descubrieron que las proposiciones geométricas pueden demostrarse deductivamente, esto es, que con sólo admitir un pequeño número de principios o axiomas, derívase luego por pura lógica todo el sistema de las demás proposiciones. Este descubrimiento tuvo efectos muy importantes; la geometría llegó a ser el modelo de ciencia deductiva, y el término del pensar estricto pasó por ser la demostración «more geométrico». Mas ¿qué son los objetos de que se ocupa la geometría científica? Filósofos y matemáticos han discutido esta cuestión en todos los sentidos y han dado gran número de respuestas. Admitíase, en general, la certeza y exactitud inatacable de las proposiciones geométricas; el problema eran tan sólo el de cómo se llega a esas proposiciones ciertas y a qué cosas se refieren estas proposiciones.

No cabe duda de que si uno admite como ciertos los axiomas geométricos, tiene por fuerza que admitir también las demás proposiciones de la geometría. Pues la concatenación de las pruebas obliga a todo el que piense lógicamente. Queda, pues, la cuestión reducida al origen de los axiomas. Estos son una serie pequeña de proposiciones sobre punto, recta, plano y otros conceptos semejantes, las cuales deben valer con plena exactitud. Por tanto, no pueden proceder de la experiencia, como la mayor parte de los asertos que establece la ciencia y la vida diaria; la experiencia, en efecto, no da sino proposiciones aproximadamente exactas, más o menos verisímiles. Hay que buscar, pues, otras fuentes de conocimiento que garanticen una certeza absoluta de las proposiciones.

Según Kant (1781), el espacio y el tiempo son formas de la intuición, son a priori, preceden a toda experiencia, y son ellas las que hacen posible, en general, la experiencia. Los objetos de la geometría, según esto, serian formas preformadas de la intuición pura, las cuales sirven de base a los juicios que fallamos sobre los objetos reales en la intuición empírica. De esta suerte, el juicio siguiente, por ejemplo: «el filo de esta regla es recto», se produce porque el filo empíricamente intuído es comparado con la intuición pura de una recta, sin que, naturalmente, este proceso se manifieste a la conciencia. El objeto de la ciencia geométrica sería, pues, la recta dada en la intuición pura; es decir, ni un concepto lógico, ni una cosa física, sino un tercero, cuya esencia sólo puede indicarse señalando a lo que el espíritu vive y siente bajo la intuición de «recta».

No vamos a pretender dar un juicio acerca de esta teoría u otras doctrinas filosóficas semejantes. Refiérense, principalmente, a la intima vivencia del espacio, la cual reside fuera de los límites de este libro. Aquí tratamos del espacio y el tiempo de la física, es decir, de una ciencia que conscientemente y con claridad creciente se aparta de la intuición, como fuente de conocimiento, y aspira a criterios más estrictos.

fig122 y fig 131

Y en este sentido debemos afirmar que nunca un físico apoyará el juicio: «el filo de esta regla es recto», sobre la inmediata intuición del «ser recto». Le es completamente indiferente que haya o no haya eso que se llama una forma pura de la intuición de lo recto, con lo cual pueda compararse el filo de la regla. El físico hará más bien distintos experimentos para comprobar la rectitud, así como comprueba por experimentos cualquier otra afirmación acerca de los objetos. Tirará, por ejemplo, una visual a lo largo del filo de la regla, es decir, determinará si un rayo luminoso que toca los puntos inicial y terminal del filo toca también los demás puntos de ese filo (fig. 130). O dará la vuelta a la regla alrededor de los puntos extremos del filo, poniendo en contacto un punto intermedio cualquiera del filo con el extremo de un indicador; si al verificar la rotación se conserva el contacto, el filo de la regla es recto (fig. 131).

Si estos métodos, desde luego muy superiores a la intuición, los sometemos ahora a la critica, veremos que propiamente nada deciden tampoco acerca de la rectitud absoluta. En el primer método supónese ya que el rayo luminoso es rectilíneo; ¿cómo se demuestra que en efecto lo es? En el segundo método se supone que los puntos de rotación de la regla y el extremo del indicador se hallan en un enlace rígido y que la recta misma es rígida; si quisiéramos comprobar la rectitud de una vara de sección circular, colocada en posición horizontal y algo curvada por el propio peso, la curvatura seguirá siendo la misma cuando hagamos girar la vara y el método del contacto reconocerá rectitud donde en realidad existe curvatura. Y no se objete que éstos son errores que se producen en toda medición física y que un experimentador hábil sabe evitar. Lo que aquí nos importa es hacer ver que nunca puede comprobarse directamente, por experiencia, la rectitud absoluta ni ninguna otra propiedad absoluta geométrica, y si sólo en relación con determinadas propiedades geométricas de los medios empleados en la medición (rectitud del rayo luminoso, rigidez del aparato). Si desnudamos las operaciones realmente verificadas y les quitamos cuanto a ellas añade el pensamiento, el recuerdo, el saber, no queda más sino la comprobación siguiente: si dos puntos del filo de la regla tocan a un rayo luminoso, también toca a él este o aquel otro punto; si dos puntos de la regla coinciden con dos puntos de un cuerpo, otro tanto vale para este o aquel tercer punto. Lo realmente comprobado son, pues, coincidencias espaciales o, mejor dicho, espaciales-temporales; esto es, la conjunción en el mismo sitio al mismo tiempo de dos puntos materiales cognoscibles. Todo lo demás es especulación, incluso el aserto tan sencillo de que por medio de experimentos de coincidencia en la regla puede establecerse la rectitud de ésta.

Un examen crítico de las ciencias exactas demuestra que todas las determinaciones vienen a parar, en general, a esas coincidencias. Toda medición es, al fin y al cabo, la comprobación de que un indicador o una señal coincide con tal o cual grado de una escala en tal o cual tiempo. Refiérase la medición a longitudes, tiempos, fuerzas, masas, corrientes eléctricas, afinidades químicas, o lo que fuere, siempre lo comprobable en realidad son coincidencias espaciales-temporales. Son, en el lenguaje de Minkowski, puntos universales que, por conjunción con líneas universales materiales, son señalados en la multiplicidad espacio-tiempo. La física es la teoría de las relaciones entre esos puntos universales señalados.

La elaboración lógica de estas relaciones es la teoría matemática; por muy complicada que sea, su fin último es siempre representar las coincidencias efectivamente observadas, como necesarias consecuencias de algunos conceptos y principios fundamentales. Algunas afirmaciones acerca de coincidencias preséntanse en la forma de proposiciones geométricas; la geometría, como doctrina aplicable al mundo real, no ocupa, pues, una situación privilegiada sobre las otras ramas de las ciencias físicas. Sus conceptuaciones son en igual manera condicionadas por el comportamiento efectivo de los objetos naturales, como los conceptos de otras esferas de la física. No podemos conceder a la geometría una situación excepcional, privilegiada.

Si la geometría de Euclides ha valido hasta ahora ilimitadamente, ello obedece al hecho empírico de que existen rayos luminosos que se comportan con gran exactitud como las rectas del esquema conceptual de la geometría euclidiana y de que hay cuerpos casi completamente rígidos que satisfacen a los axiomas euclidianos de la congruencia. A la afirmación de que la geometría posee una validez absoluta no podemos darle, desde el punto de vista físico, ningún sentido aprehensible.

Los objetos de la geometría efectivamente aplicada al mundo de las cosas son, pues, estas cosas mismas consideradas desde un determinado punto de vista. La línea recta es, por definición, el rayo luminoso o la trayectoria de inercia, o la totalidad de los puntos de un cuerpo considerado como rígido, cuando no se mueven al girar alrededor de dos puntos fijos, o cualquier otro «algo» físico. La recta así definida ¿tiene las propiedades que afirma la geometría de Euclides? Sólo la experiencia puede decidirlo. Una propiedad de la geometría euclidiana es el teorema de la suma de los ángulos del triángulo, que Gauss ha examinado empíricamente; debemos reconocer que esos experimentos estaban justificados. Otra propiedad característica de la geometría de dos dimensiones fué dada en el encaje perfecto del hexágono de cuerdas (pág. 338). Sólo la experiencia puede enseñarnos si determinada especie de realización de la recta, de la unidad de longitud, etc., por determinadas cosas físicas tiene o no esa propiedad. En el primer caso es aplicable la geometría euclidiana relativamente a esas definiciones; en el segundo caso, no.

Einstein afirma que todas las definiciones dadas hasta ahora de los conceptos fundamentales del continuo espacio-tiempo, por medio de metros rígidos, relojes, rayos luminosos, trayectorias de inercia, satisfacen a las leyes de la geometría euclidiana y, respectivamente, del universo de Minkowski; pero sólo en limitadas, en pequeñas esferas, no en lo grande. Si los errores no han sido hasta ahora descubiertos, débese a lo pequeños, casi insignificantes, que son. Para acudir a remediarlos ofrécense dos caminos: o bien se deja ya de definir la recta por el rayo luminoso, la longitud por el cuerpo rígido, etc., y se buscan otras realizaciones de los conceptos euclidianos fundamentales, para poder atenerse al sistema euclidiano de sus conexiones lógicas, o se abandona la geometría euclidiana misma y se va al establecimiento de una nueva teoría general del espacio.

Pero el primer camino no puede seriamente aconsejarse; eso lo ve fácilmente cualquiera que no sea enteramente profano en la ciencia. Sin embargo, no puede tampoco demostrarse que sea imposible de seguir. No decide en este punto la lógica, sino el tacto científico. No hay un camino lógico que de los hechos conduzca a la teoría. La ocurrencia, la intuición, la fantasía, son aquí, como doquiera, las fuentes de la labor creadora, y el criterio de la exactitud es la predicción profética de procesos futuros o aun no investigados. Que el lector ensaye la hipótesis siguiente: «el rayo luminoso, en el espacio cósmico vacío, no es el más recto que hay», y luego reflexione sobre las consecuencias de tal hipótesis; comprenderá entonces que Einstein no haya seguido el primer camino.

Puesto que faltaba la geometría euclidiana, hubiera podido elegir otra geometría determinada no euclidiana. Existen tales sistemas de conceptos, construidos por Lobatschewski (1829), Bolyai (1832), Riemann (1854), Helmholtz (1866) y otros, que fueron inventados propiamente para ver si determinados axiomas de Euclides son necesarias consecuencias de los demás; si lo fueran, habría de llegarse a contradicciones lógicas al substituirlos por otros axiomas. Pero elegir alguna de esas geometrías especiales no euclidianas, para representar el universo físico, fuera remediar un daño con otro daño. Einstein retrocedió hasta el fenómeno humano de la física, la coincidencia espacial temporal, el suceso, el punto universal.

7. La métrica del continuo espacio-tiempo.

La totalidad de los puntos universales señalados es lo efectivamente determinable. El continuo espacio-tiempo de cuatro dimensiones carece de estructura en sí y por sí; las relaciones efectivas de los puntos universales en él, relaciones que el experimento descubre, son las que le imprimen una determinación de medidas y una geometría. Tenemos, pues, en el mundo real, ante nosotros, las mismas circunstancias que acabamos de ver al considerar la geometría de las superficies. El método para tratarlas matemáticamente habrá de ser el mismo.

Lo primero será introducir coordenadas gaussianas en el universo de cuatro dimensiones. Construímos una red de puntos universales señalados; esto significa que imaginamos el espacio lleno de materia en cualquier movimiento, de materia que puede revolverse y deformarse, pero que ha de conservar siempre su constante conexión, una especie de «molusco», como dice Einstein; en ella trazamos tres grupos de lineas que se entrecruzan y que numeramos, distinguiéndolas por medio de las letras x, y, z. En las esquinas de la red que así va formándose imaginemos relojes, con una marcha cualquiera, pero tales que la diferencia de los datos t de los relojes próximos sea pequeña. El conjunto es, pues, un sistema de referencia sin rigidez, un «molusco de referencia». En el universo de cuatro dimensiones le corresponde un sistema de coordenadas gaussianas consistente en una red de cuatro grupos de superficies numeradas x, y, z, t.

Todos los sistemas rígidos en movimiento son, naturalmente, especies particulares de esos sistemas que se deforman. Pero desde nuestro punto de vista general es absurdo introducir la rigidez como algo dado a priori. La separación de espacio y tiempo es también enteramente caprichosa; pues debiendo admitirse que la marcha de los relojes es enteramente caprichosa, aunque constantemente variable, resulta que el espacio, como totalidad de todos los puntos universales «simultáneos», no tiene realidad física. Si elegimos otras coordenadas gaussianas, otros serán los puntos universales simultáneos.

Pero las que no se alteran, al trasladarse de uno a otro sistema de coordenadas gaussianas, son las intersecciones de las líneas universales reales, los puntos universales señalados, las coincidencias espaciales temporales. Todos los hechos de la física, verdaderamente.comprobables, son relaciones cualitativas de situación entre esos puntos universales y, por tanto, permanecen intactas aun cuando cambien las coordenadas de Gauss.

Tal transformación de las coordenadas gaussianas, en el continuo espacio-tiempo, significa el tránsito de un sistema de referencia a otro deformado caprichosamente y en un movimiento cualquiera. La exigencia de no admitir en las leyes naturales nada más que lo que realmente sea determinable conduce, pues, a que las tales leyes deban ser invariantes con respecto a cualesquiera transformaciones de las coordenadas gaussianas x, y, z, t en otras x', y', z', t'. Este postulado contiene evidentemente el principio general de la relatividad, pues entre las transformaciones de x, y, z, t hállanse las que representan el paso de un sistema de referencia tridimensional a otro en movimiento cualquiera; pero formalmente va aún más allá, puesto que incluye deformaciones cualesquiera del espacio y del tiempo.

Así tenemos ya el fundamento de la teoría general del espacio; sólo en él es posible desenvolver la integral relatividad. Ahora se tratará de enlazar este método matemático con las reflexiones físicas que antes hemos hecho y que culminaron en el establecimiento del principio de la equivalencia.

Ahora estamos ya, con relación al mundo cuatridimensional, en la misma situación que el agrimensor en el monte, cuando ya ha establecido su red de coordenadas, pero aun no ha empezado a medir el terreno con su cinta métrica. Debemos ahora buscar una cinta métrica de cuatro dimensiones.

Puede servirnos el principio de la equivalencia. Sabemos que, eligiendo convenientemente el sistema de referencia, siempre es posible conseguir que, en un trozo bastante pequeño del universo, no haya campo gravitatorio. Hay infinitos sistemas de referencia tales que se mueven con movimiento rectilíneo y uniforme relativamente unos a otros y para los cuales son válidas las leyes de la teoría especial de la relatividad. Los metros y los relojes se conducen tal como dicen las transformaciones de Lorentz; los rayos luminosos y los movimientos de inercia (pág. 326) son líneas universales rectas. Dentro, pues, de ese pequeño trozo del universo, la magnitud

$G=s^{2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}$

es una invariante de significación física inmediata. Si, en efecto, la unión del punto cero O (que se admite en el interior del pequeño trozo del universo) con el punto universal P (x, y, z, t) es una línea universal de espacio, entonces es s la distancia OP, en el sistema de referencia en que los dos puntos sean simultáneos; si la línea universal OP es una línea de tiempo, entonces es s = ict, siendo t la diferencia de tiempo entre los sucesos OP, en el sistema de coordenadas en que ambos se verifiquen en el mismo lugar. Ya antes (VI, 10, pág. 317) hemos llamado a s la distancia cuatridimensional; es directamente mensurable con metros y relojes, y, además, si se introduce la coordenada imaginaria u = ict, tiene formalmente el carácter de una distancia euclidiana en el espacio de cuatro dimensiones:

$s={\sqrt {G}}={\sqrt {x^{2}+y^{2}+z^{2}+u^{2}}}$.

El hecho de que la teoría especial de la relatividad valga en lo pequeño, corresponde exactamente a la aplicabilidad de la geometría euclidiana a pedazos suficientemente pequeños de una superficie cualquiera. Pero no es preciso que la geometría euclidiana, y respectivamente la teoría especial de la relatividad valgan también en lo grande; no hace falta que haya líneas universales rectas, con tal de que haya lineas geodésicas.

fig132

El posterior tratamiento del universo cuatridimensional sigue paralelo a la teoría de las superficies. Lo primero es medir las mallas de una red cualquiera de coordenadas gaussianas por medio de la distancia cuatridimensional s. Interpretaremos el procedimiento en un plano xt de dos dimensiones (fig. 132). Una malla de la red de coordenadas es limitada por las lineas x = 3, x = 4 y t = 7, t = 8 (compárese figura 127 en la página 334). Los rayos luminosos que parten del punto intersección x = 3, t = 7 corresponden a dos lineas universales que se cruzan y que, dentro de un espacio pequeño, podemos dibujar como rectas cortadas a 90°. Entre esas líneas luminosas pasan las curvas hiperbólicas $G=\pm 1$; corresponden al círculo que, en la geometría corriente, contiene los puntos de igual distancia 1.

Si trasladamos aquí la fórmula [87] de la teoría de las superficies obtenemos, para la invariante s, la expresión

$s^{2}=g_{11}x^{2}+2g_{12}xu+g_{22}u^{2}$,

siendo x y u = ict las coordenadas gaussianas de un punto cualquiera P de la malla en cuestión.

Si ahora ponemos, en lugar de u, ict, tenemos

$s^{2}=g_{11}x^{2}+2icg_{12}xt-c^{2}g_{22}t^{2}$,

o con otra designación de los factores:

$s^{2}=g_{11}x^{2}+2g_{12}xt+g_{22}t^{2}$.

Los g₁₁, g₁₂ y g₂₂ llámanse factores determinativos de la medida y pueden interpretarse directamente en sentido físico. Así, por ejemplo, para t = 0, s es igual a ${\sqrt {g_{11}x}}$, es decir, ${\sqrt {g_{11}}}$ significa la longitud verdadera del lado espacial de la malla en el sistema de referencia en que esta inmóvil.

En el universo de cuatro dimensiones, la distancia invariante s entre dos puntos, cuyas coordenadas gaussianas relativas son x, y, z, t, quedará representada por una expresión de la forma:

${\begin{aligned}s^{2}&=g_{11}x^{2}+g_{22}y^{2}+g_{33}z^{2}+g_{44}t^{2}\\&+2g_{12}xy+2g_{13}xz+2g_{14}xt\\&+2g_{23}yz+2g_{24}yt+2g_{34}zt\end{aligned}}$.[88]

Podemos llamar a esta fórmula el teorema de Pitágoras generalizado para el universo de cuatro dimensiones. Las magnitudes g₁₁....g₃₄ son los factores determinativos de la medida; tendrán, en general, distintos valores de malla en malla en la red de coordenadas. También tendrán valores distintos si se eligen otras coordenadas gaussianas; pero estos valores están en relación con los primeros por medio de determinadas fórmulas de transformación.

8. Las leyes fundamentales de la nueva mecánica.

Según el principio general de la relatividad, las leyes naturales represéntanse por invariantes respecto de cualquier transformación de las coordenadas gaussianas, exactamente como las propiedades geométricas de una superficie son invariantes con respecto a cualesquiera transformaciones de las coordenadas curvas. La armazón de la teoría de las superficies constituíanla las lineas geodésicas. De igual modo, en el universo cuatridimensional, construiremos líneas geodésicas, es decir, líneas universales que forman la unión más corta entre dos puntos universales; en este caso la distancia entre dos puntos próximos ha de medirse por la invariante s.

¿Qué significan las líneas geodésicas? Es claro que en territorios tales que, merced a una conveniente elección del sistema de referencia, no tengan gravitación, esas líneas son rectas relativamente a ese sistema; las líneas universales rectas son, empero, ora de espacio (s² > 0), ora de tiempo (s² < 0) o lineas luminosas (s = 0). Si se introduce otro sistema de coordenadas gaussianas, esas mismas líneas universales tórnanse ahora curvas; pero siguen siendo, como es natural, líneas geodésicas.

De aquí se deriva que las líneas geodésicas han de representar precisamente los procesos físicos, que en la geometría y en la mecánica corriente son representados por líneas rectas: rayos luminosos y movimientos de inercia. Con esto hemos encontrado la formulación que buscábamos para la ley de inercia generalizada, que comprende los fenómenos de inercia y de gravitación en una sola expresión.

Si conocemos los factores determinativos de la medida g₁₁....g₃₄ relativamente a cualquier sistema de coordenadas gaussianas, para cada lugar de la red, podremos hallar las líneas geodésicas por puro cálculo. Si en un territorio no existe campo gravitativo relativamente al sistema de coordenadas considerado, entonces son

${\begin{aligned}g_{11}=g_{22}=g_{33}=1,\quad g_{44}=-c^{2},\\g_{12}=g_{13}=g_{14}=g_{23}=g_{24}=g_{34}=0,\end{aligned}}$[89]

pues en tal caso redúcese la expresión general de la distancia (88) a

$s^{2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}$

Si, pues, las g se apartan de esos valores, ello significa ese estado que en la mecánica corriente se caracteriza como campo gravitatorio; los movimientos de inercia son entonces no uniformes y curvos, para explicar lo cual la mecánica corriente de Newton acude a la fuerza de atracción como causa. Las diez magnitudes g tienen, pues, una función doble: 1.° definen la determinación de la medida, las unidades de longitudes y tiempos; 2.°, representan el campo gravitatorio de la mecánica ordinaria. Dicese: las g determinan el campo métrico o campo gravitatorio.

La teoría de Einstein es, pues, una mezcla extraña y admirable de geometría y física, una síntesis de las leyes de Pitágoras y de Newton. A tal punto llega por medio de una purificación fundamental de los conceptos espacio y tiempo, quitándoles los añadidos que proceden de la intuición subjetiva, merced a la más completa relativización y objetivación que cabe pensar. Esta es la importancia y significación de la doctrina nueva, para el desarrollo espiritual de la humanidad.

La nueva fórmula de la ley de inercia no es, empero, mas que el primer peso de la teoría. Hemos introducido conceptualmente las g; hemos reconocido en ellas el medio de describir matemáticamente el estado geométrico mecánico del universo relativamente a cualquier sistema de coordenadas gaussianas. Ahora es cuando se presenta el problema propio de la teoría.

Deben hallarse las leyes según las cuales pueda determinarse el campo métrico (las g), para cada lugar del continuo espacio-tiempo, relativamente a cualquier sistema de coordenadas gaussianas.

Sobre las leyes sabemos, por ahora, lo siguiente:

1.° Tienen que ser invariantes respecto de cualquier cambio de las coordenadas gaussianas.

2.° Tienen que estar integramente determinadas por la distribución de los cuerpos materiales.

Añádase a éstas una condición formal, que Einstein ha tomado de la teoría ordinaria de la gravitación establecida por Newton. Si esta teoría se representa por ecuaciones diferenciales, como teoría de seudoacción próxima, estas ecuaciones son, como todas las leyes físicas que a campos se refieren, del segundo orden; y habrá que pedir que las nuevas leyes de la gravitación, que son ecuaciones diferenciales para las g, sean igualmente, a lo sumo, del segundo orden.

Einstein ha conseguido derivar de estas exigencias las ecuaciones del campo métrico o campo gravita torio. Hilbert, Klein, Weyl y otros matemáticos han colaborado en ello y han investigado y establecido la estructura formal de las fórmulas de Einstein. Hemos de renunciar a comunicar aquí esas leyes y su funda mentación, pues no podría hacerse sin emplear la alta matemática. Basten algunas indicaciones.

Sabemos, por la teoría de las superficies, que la curvatura es una invariante, con respecto a cualquier cambio de las coordenadas gaussianas, la cual, por mediciones en la superficie misma, puede determinarse; recuerde el lector el hexágono de cuerdas.

Por modo análogo pueden hallarse para el universo de cuatro dimensiones invariantes que son directas generalizaciones de la invariante de curvatura en la teoría de las superficies. Pueden pensarse del siguiente modo, aproximadamente: de un punto P del mundo de cuatro dimensiones háganse partir todas las lineas geodésicas que toquen a una superficie de dos dimensiones que pase por P; estas líneas geodésicas llenan a su vez una superficie que podría llamarse superficie geodésica. Si en ésta se coloca un hexágono, cuyos lados y radios tengan la misma longitud cuatridimensional, este hexágono, en general, no encajará; la superficie geodésica es, pues, curva. Si por el punto P se orienta la superficie geodésica de distinto modo en el espacio cuatridimensional, variará la curvatura. La totalidad de las curvaturas de todas las superficies geodésicas por un punto proporciona un número de invariantes independientes. Si éstas son cero, las superficies geodésicas son planas y el espacio cuatridimensional es euclidiano.

Si las invariantes se apartan del cero, esos apartamientos determinan, pues, los campos gravitatorios y deben depender de la distribución de los cuerpos materiales. Pero la masa de un cuerpo puede concebirse, según la teoría especial de la relatividad (VI, 8, fórmula [83], pág. 299), como componente temporal de la impulsión, y es igual a la energía dividida por el cuadrado de la velocidad de la luz; la distribución de la materia está, pues, determinada por ciertas invariantes de energía-impulsión. Estas son las invariantes a las cuales hay que poner como proporcionales las invariantes de curvatura. El factor de proporcionalidad corresponde a la constante de gravitación (III, 3, pág. 78) de la teoría de Newton. Las fórmulas a que se llega así son las ecuaciones del campo métrico. Dada la distribución espacial-temporal de la energía y de la impulsión, pueden calcularse las g, y éstas, a su vez, el movimiento de los cuerpos materiales y la distribución de su energía. El conjunto es un sistema complicadísimo de ecuaciones diferenciales; pero esta complicación matemática está compensada por el enorme progreso conceptual, que consiste en su invariancia general. Pues ésta es la expresión de la integral relatividad de todos los procesos; el espacio absoluto queda definitivamente excluido de las leyes físicas.

Debemos aún ocuparnos de una forma de expresión que, por lo común, escandaliza a los que no son matemáticos. Las invariantes del espacio tridimensional o del universo cuatridimensional, análogas a la curvatura de las superficies, suelen designarse también con el nombre de medida de curvatura; dícese de terrenos espaciales-temporales, donde esa medida es diferente de cero, que son «curvos». Contra esto se alza indignado generalmente el ánimo del indocto: «puedo representarme muy bien que en el espacio haya algo que sea curvo, pero que el espacio mismo sea curvo es absurdo». Pero nadie pide que eso sea objeto de una representación; ¿puede nadie representarse luz invisible y sonidos inaudibles? Si se admite que en esto fallan los sentidos y siguen valiendo los métodos de la física, habrá que decidirse a admitir lo mismo para la teoría del espacio y del tiempo. La intuición no percibe sino lo que se produce y se da efectivamente como proceso espiritual, merced a la acción concertada de procesos físicos, fisiológicos y psíquicos; la física no niega que eso que nos es efectivamente dado pueda interpretarse con gran exactitud según las leyes clásicas de Euclides. Las desviaciones que la teoría de Einstein anuncia son tan nimias, que sólo la extraordinaria precisión de la física y de la astronomía actuales puede manifestarlas. Pero existen, y si la suma de las experiencias conduce al resultado de que el continuo espacio-tiempo es no euclidiano, o «curvo», debe la intuición inclinarse ante el juicio del conocimiento.

9. Consecuencias y comprobaciones mecánicas.

El primer cometido de la nueva física es demostrar que la mecánica y la física clásica es exacta con gran aproximación; pues de otro modo no podría comprenderse que dos siglos de incansable y cuidadosa investigación se hubieran satisfecho con ellas. El segundo problema es hallar desviaciones que sean características de la nueva teoría y puedan servir a comprobarla en la experiencia.

¿Por qué la mecánica clásica es bastante para exponer todos los procesos terrestres y casi todos los procesos cósmicos de movimiento? ¿Qué es lo que substituye a los conceptos del espacio absoluto y del tiempo absoluto, sin los cuales, según los principios de Newton, no pueden explicarse los más sencillos hechos, como el péndulo de Foucault, las fuerzas de inercia y centrífugas?

En el fondo, ya hemos contestado a estas preguntas al comienzo de nuestras explicaciones sobre el principio general de la relatividad. Allí (VII, 1, pág. 319) hemos establecido, como fundamento de la dinámica relativista, la afirmación de que en el lugar del espacio absoluto, como causa ficticia de procesos físicos, han de aparecer ahora masas lejanas como causas reales. El Cosmos en conjunto, el ejército de los astros, produce en todo lugar y en todo tiempo un determinado campo métrico o campo gravitatorio; su constitución no puede enseñárnosla mas que una especulación de índole cosmológica, como la que luego habremos de explicar (VII, 11, pág. 370). Pero, en pequeño, eligiendo convenientemente el sistema de referencia, el campo métrico debe ser «euclidiano», es decir, que las trayectorias de inercia y los rayos luminosos serán líneas universales rectas. Comparadas con el Cosmos, son, empero, las dimensiones de nuestro sistema planetario mismo harto pequeñas; y por eso, si las referimos a un sistema de referencia adecuado, valen en él las leyes de Newton hasta donde el Sol o las masas planetarias no producen perturbaciones locales, que corresponden a las atracciones de la teoría de Newton. La astronomía enseña que semejante sistema de referencia, en el cual la acción de las masas de las estrellas fijas dentro de los límites de nuestro sistema planetario conduce a la determinación euclidiana de las medidas, está justamente en reposo relativo (o en movimiento uniforme y rectilíneo) respecto a la totalidad de las masas cósmicas y que, por tanto, las estrellas fijas, con referencia a ese sistema, hacen movimientos relativamente pequeños que en el centro se suprimen; una explicación de este hecho astronómico sólo puede darse aplicando los nuevos principios dinámicos al conjunto del Cosmos, lo cual será objeto de nuestros últimos capítulos. Ahora debemos ocuparnos, ante todo, de la mecánica y la física dentro del sistema planetario. Y en tal caso, las teorías de la mecánica de Newton siguen casi intactas; pero hay que tener siempre en cuenta que el plano de oscilación del péndulo de Foucault no es fijo con respecto al espacio absoluto, sino con respecto al sistema de las masas lejanas y que las fuerzas centrífugas no se presentan en rotaciones absolutas, sino en rotaciones relativas a las masas lejanas. Además, es completamente lícito no referir las leyes de la física al habitual sistema de coordenadas, en el cual el campo métrico es euclidiano y no existe campo gravitatorio en el sentido corriente (hasta los campos locales de las masas planetarias), sino a un sistema que se halle en movimiento (o incluso que se deforme); pero en este caso manifiéstanse al punto campos gravitatorios, y la geometría pierde su carácter euclidiano. La forma general de las leyes naturales sigue siendo la misma siempre; pero los valores de las magnitudes g₁₁, g₁₂....g₃₄...., que determinan el campo métrico o campo gravitatorio, son distintos en cada sistema de referencia. En esta invariancia de las leyes consiste la diferencia que separa la nueva de la antigua dinámica; en la antigua era posible, naturalmente, pasar a cualesquiera sistemas de referencia movidos (o deformados); pero las leyes naturales no conservaban entonces su forma; había formas de las leyes naturales que eran «las más sencillas», las que se tomaban en sistemas de coordenadas inmóviles en determinado espacio, en el espacio absoluto. En la teoría general de la relatividad no hay tales formas privilegiadas, que sean «las más sencillas», de las leyes naturales; a lo sumo, pueden los valores numéricos de las magnitudes g₁₁....g₃₄, que aparecen en todas las leyes naturales, ser particularmente sencillos o alejarse poco de tales sencillos valores, dentro de limitados territorios. Así, la astronomía refiere sus fórmulas a un sistema de referencia que, dentro del pequeño espacio del sistema planetario, seria euclidiano si no existieran el Sol y los planetas, un sistema, pues, en que las g₁₁....g₃₄ tendrían los valores sencillos expresados en la fórmula [89] (pág. 352). Pero, en realidad, las g₁₁....g₃₄ no tienen esos valores, sino que en la proximidad de las masas planetarias aléjanse un poco de ellos, como luego explicaremos más detenidamente. Cualquier otro sistema de referencia (por ejemplo, uno en movimiento de rotación) en el cual las g₁₁....g₃₄, aun sin masas planetarias, no tuvieran los sencillos valores de la fórmula [89], es, pues, en principio, tan legítimo como el otro. Esto nos autoriza, si queremos, a volver al punto de vista ptolemaico de la Tierra inmóvil; ello significaría el empleo de un sistema de referencia fijo en la Tierra, en el cual las g₁₁....g₃₄ reciben valores tales que correspondan al campo centrífugo de rotación con respecto a las masas lejanas. Desde la cumbre alta donde ha llevado Einstein a la física aparécennos ahora Ptolomeo y Copérnico con igual derecho; los dos puntos de vista dan las mismas leyes naturales, sólo que con distintos valores numéricos de las g₁₁....g₃₂. La elección de tal o cual punto de vista no depende de principios; es cuestión de comodidad. Para la mecánica del sistema planetario, la concepción de Copérnico es, desde luego, la más cómoda. Pero es absurdo calificar de «ficticios», en oposición a otros producidos por masas próximas y calificadas de «reales», los campos gravitatorios que aparecen al elegir otro sistema de referencia; tan absurdo como es, en la teoría especial de la relatividad, la cuestión de la longitud «real» de una vara (VI, 5, pág. 278). Un campo gravitatorio no es en sí ni real ni ficticio; no tiene significación alguna independiente de la elección de las coordenadas, exactamente lo mismo que la longitud de una vara. Tampoco se distinguen los campos en que unos sean producidos por masas y otros no; lo que sucede es que en un caso son, sobre todo, las masas próximas, y en el otro, solamente las masas lejanas del Cosmos.

Contra esta teoría se han dado argumentos «de sentido común»; entre otros, el siguiente: Supongamos un tren que choca contra un obstáculo; en el tren se producen grandes trastornos y ruinas; el proceso puede describirse de dos maneras: o bien se toma la Tierra (que aquí es considerada como inmóvil relativamente a las masas cósmicas) como sistema de referencia y se hace responsable del desastre a la aceleración (negativa) del tren, o bien se elige un sistema de referencia fijo en el tren, y entonces, en el momento del choque, el universo entero da una sacudida y aparece un campo gravitatorio muy fuerte dirigido paralelamente al movimiento primitivo; y ese campo gravitatorio produce los desperfectos en el tren. Pero entonces ¿cómo es que no se derrumba igualmente la iglesia de la aldea vecina? ¿Por qué las consecuencias de la sacudida y del campo gravitatorio, unido a ella, no se hacen notar mas que en el tren, si, en efecto, son igualmente legitimas estas dos aserciones: 1.ª, el universo está en reposo y el tren experimenta un frenazo; 2.ª, el tren está en reposo y el universo experimenta un frenazo? La respuesta a la objeción es la siguiente: La iglesia no se derrumba porque, al frenar el universo su movimiento, la situación relativa de la iglesia respecto a las masas cósmicas lejanas no es alterada; la sacudida que, visto el caso desde el tren, experimenta el universo entero alcanza por igual a todos los cuerpos, hasta las más lejanas estrellas, incluyendo también a la iglesia; todos esos cuerpos caen libremente en el campo gravitatorio, que se presenta al frenar el universo su movimiento; sólo uno, el tren, es impedido en su caída libre por las fuerzas frenadoras. Pero los cuerpos que caen libremente compórtanse, con relación a los procesos interiores (como lo es el equilibrio de la iglesia sobre la tierra), exactamente igual que los cuerpos que van libremente, exentos de todo influjo exterior; no se presentan, pues, perturbaciones del equilibrio, y la iglesia no se derrumba. En cambio, el tren es impedido en su libre caída; de aquí nacen fuerzas y tensiones que dan lugar a las consecuencias destructoras.

Apelar al «sentido común» en estos difíciles problemas es muy arriesgado. Hay partidarios del éter substancial que se oponen a la teoría de la relatividad porque no es bastante intuitiva, imaginativa, para su gusto. Muchos de éstos han reconocido exclusivamente el principio especial de la relatividad, después que los experimentos, por modo unívoco, hubieron decidido en su favor; pero todavía se rebelan contra el principio general de la relatividad, porque les parece contrario al sentido común. A éstos dedica Einstein la reflexión siguiente: según la teoría especial de la relatividad, el tren que marcha con movimiento uniforme es un sistema de referencia tan legítimo como la Tierra. ¿Lo admitirá así el sentido común del maquinista? El maquinista objetará que él no calienta y engrasa mas que la locomotora y no la «comarca» por que atraviesa, y que, por tanto, la locomotora y no la Tierra debe ser la que, por su movimiento, patentiza el resultado de su trabajo. Semejante aplicación del «sentido común» llevada, en último término, a la negación de todo sentido científico; pues ¿de qué sirve—pregunta el sentido común del hombre ordinario—ocuparse de la relatividad o de los rayos catódicos, si tal actividad, evidentemente, no es propia para ganar dinero?

Continuemos ahora considerando la mecánica celeste desde el punto de vista de Einstein, y pasemos a los campos gravitatorios locales, que, a consecuencia de existir masas planetarias, se asientan en el campo cósmico.

No podemos extendernos mucho sobre estas investigaciones de Einstein, porque en ellas se trata principalmente de deducciones matemáticas inferidas de las ecuaciones de los campos.

El problema más sencillo es determinar el movimiento de un planeta alrededor del Sol. Lo más cómodo es partir del ya citado sistema de coordenadas gaussianas, en el cual, en la comarca del sistema solar y en ausencia del Sol y de los planetas, el campo métrico sería euclidiano y no existiría campo gravitatorio alguno en el sentido corriente; ese sistema se caracteriza porque, si no se considera la acción del Sol, las g₁₁....g₃₄ tendrían los valores de la fórmula [89] (pág. 352). Trátase, pues, de determinar cuánto las g₁₁....g₃₄ se alejan de esos valores por causa de la masa solar; sirven para esto muy bien las ecuaciones de los campos establecidas por Einstein, y se demuestra que admitiendo que la masa solar, y con ella también el campo, se propaga simétricamente en modo esférico, obtiénense expresiones muy determinadas y relativamente sencillas para las g₁₁....g₃₄. Luego pueden calcularse las trayectorias de los planetas como líneas geodésicas de esa determinación de las medidas. Su curvatura, que en la teoría de Newton es considerada como efecto de la fuerza atractiva, aparece en la teoría de Einstein como consecuencia de la curvatura del universo espacio-tiempo, cuyas líneas geodésicas son.

El cálculo da por resultado determinadas trayectorias planetarias, que son, muy aproximadamente, las mismas que en la teoría de Newton. Este resultado es admirable, si se recuerda cuán diferentes son los puntos de vista de que parten ambas doctrinas. Newton parte del espacio absoluto, engendro que no satisface a la crítica del conocimiento, y de una fuerza desviadora inventada ad hoc y provista de la extraña y notable propiedad de ser proporcional a la masa inerte. Einstein parte de un principio general que satisface las exigencias de la crítica del conocimiento, y no hace ninguna hipótesis especial. Aun cuando la teoría de Einstein no hiciera otra cosa que someter la mecánica de Newton al principio general de la relatividad, habrían de preferirla siempre quienes busquen en las leyes de la naturaleza la armonía de la sencillaz suprema.

Pero la teoría de Einstein hace más. Contiene, como ya hemos dicho, las leyes que Newton da de las trayectorias planetarias; pero las contiene aproximadamente; las leyes exactas son algo distintas, y la diferencia es tanto mayor cuanto más cercano al Sol se encuentra el planeta. Ya hemos visto, al estudiar la mecánica celeste de Newton (III, 4, pág. 78), que ésta falla justamente en el planeta más próximo al Sol, en Mercurio; queda sin explicar un movimiento del perihelio de Mercurio de 43 segundos de arco por siglo. Precisamente esta cantidad exige la teoría de Einstein, que de esta suerte está comprobada de antemano por los cálculos de Leverrier. Este resultado es de extraordinario peso, pues en la fórmula de Einstein no entra ninguna constante nueva, arbitraria, y la «anomalía» de Mercurio es una consecuencia tan necesaria de la teoría como lo es asimismo la validez de las leyes de Keplero para los planetas más lejanos del Sol.

10. Consecuencias y comprobaciones ópticas.

Además de estas consecuencias astronómicas, sólo se han encontrado hasta ahora algunos fenómenos ópticos que no eludan, por su pequeñez, la observación.:

Uno es el corrimiento hacia el rojo de las rayas espectrales de la luz procedente de astros de masa grande. En la superficie de éstos hay un campo gravitatorio muy fuerte, que altera la determinación de las medidas y es causa de que un reloj en él andaría más despacio que en la Tierra, donde el campo gravitatorio es menor. Pero disponemos de relojes tales en los átomos y moléculas de los gases; el mecanismo vibratorio en éstos es, de seguro, el mismo hállese la molécula donde se halle, y la duración de la vibración es, pues, igual en los sistemas de referencia que tengan el mismo campo gravitatorio; por ejemplo, un campo igual a cero.

Sea T la duración de la vibración en un espacio sin campo. Será entonces s = icT la distancia invariante que corresponda a los dos puntos universales constituidos por dos puntos consecutivos de retroceso de la vibración, relativamente al sistema de referencia en donde el átomo está en reposo. En un sistema de referencia relativamente acelerado, en el cual hay un campo gravitatorio, s = icT estará dado por la fórmula [88], donde x, y, z caracterizan la posición del átomo y t el tiempo de vibración medido en ese sistema. Podemos poner x = y = z = 0, situando el punto cero de las coordenadas espaciales en el átomo mismo; entonces,

$s^{2}=-c^{2}T^{2}=g_{44}t^{2}$

esto es,

$t=T{\frac {c}{\sqrt {-g_{44}}}}$

Ahora bien; en el espacio sin campo es g₄₄ = -c² (véase fórmula [89], pág. 352), y, por tanto, t = T. Pero en el campo gravitatorio es g₄₄ distinto de -c²; por ejemplo, g₄₄ = -c²(1 - γ); la duración de la vibración está, pues, cambiada, y es igual a

$t=T{\frac {1}{\sqrt {1-\gamma }}}$,

o, si la desviación γ es pequeña, aproximadamente (véase nota a la pág. 237):

$t=T\left(1+{\frac {\gamma }{2}}\right)$.[90]

Esta es la diferencia en la marcha de dos relojes que se encuentran en dos distintos lugares, para los cuales la diferencia del campo gravitatorio medido por g₄₄ tiene el valor relativo γ.

Puede saberse si γ es positivo o negativo considerando un caso sencillo en el que la cuestión pueda resolverse directamente merced al principio de equivalencia. Ello se consigue para un campo gravitatorio constante, como el que existe inmediatamente en la superficie de un cuerpo celeste. La acción de ese campo g puede substituirse por una aceleración del observador dirigida contra la atracción y de la misma cantidad g. Sea l la distancia entre el observador y la superficie del astro; una onda luminosa procedente del astro necesitará para llegar al observador el tiempo $t={\tfrac {l}{c}}$, y el observador percibirá la onda como si durante este tiempo él mismo hubiese realizado hacia afuera un movimiento acelerado con la aceleración g. Entonces, al llegar a él la onda luminosa tendrá él la velocidad $v=gt={\tfrac {gl}{c}}$ en la dirección del movimiento de la luz, por lo cual observará, según el principio de Doppler (fórmula [36], pág. 143), un número de vibraciones menor:

$\nu '=\nu \left(1-{\frac {v}{c}}\right)=\nu \left(1-{\frac {gl}{c^{2}}}\right)$.

Así, pues, la duración de la vibración $t={\tfrac {1}{\nu '}}$, observada en el campo gravitatorio, hállase, en relación con el $T={\tfrac {1}{\nu }}$, determinado en el espacio sin campo, por el modo siguiente:

$t=T{\frac {1}{1-{\frac {gl}{c^{2}}}}}$,

o aproximadamente:

$t=T\left(1+{\frac {gl}{c^{2}}}\right)$.[91]

Esta fórmula da, en general, la diferencia de marcha de dos relojes que se encuentran en un campo gravitatorio constante g a la distancia l.

En el campo gravitatorio constante es, según esto, positiva la magnitud γ, que aparece en la fórmula [90], y cuyo valor es, según la fórmula [91], $\gamma ={\tfrac {2gl}{c^{2}}}$. La duración de la vibración y, por tanto, la longitud de onda es, pues, aumentada por el campo, para una onda luminosa que marche contra la atracción del campo gravitatorio. Este resultado puede trasladarse a la luz procedente de los astros; la magnitud γ será positiva. Por donde resultará que todas las rayas del espectro estarán corridas hacia el rojo. Aun cuando este efecto es muy pequeño, su existencia se afirma hoy como muy verosímil tanto en el Sol como en las estrellas fijas.

Podemos en este momento llenar un vacío que dejamos en otro lugar anterior (VI, 5, pág. 280); esto es, explicar enteramente la llamada «paradoja de los relojes». Suponíamos dos observadores A y B, uno de los cuales permanece inmóvil en un sistema inercial (de la teoría especial de la relatividad), mientras el otro hace un viaje. Al regreso de B, el reloj de A, según la fórmula [69], anda adelantado respecto del de B en la cantidad ${\tfrac {\beta ^{2}}{2}}t$, siendo t el tiempo total del viaje, medido en el sistema A; esta fórmula desde luego es sólo aproximada; pero basta para nuestros fines, si hacemos todos los demás cálculos con la correspondiente aproximación.

Ahora bien; cabe considerar B como inmóvil; entonces A hace un viaje en la dirección opuesta. Pero no es lícito concluir simplemente que ahora el reloj de B debe adelantar sobre el de A la misma cantidad, pues B no descansa en un sistema inercial, sino que sufre aceleraciones.

Desde el punto de vista de la teoría general de la relatividad hay que atender a que, al variar de sistema de referencia, deben introducirse determinados campos gravitatorios durante los tiempos de aceleración.

En la primera consideración hállase inmóvil A en un espacio en el que domina la determinación euclidiana de las medidas y no existen campos gravitatorios; en la segunda consideración descansa B en un sistema de referencia en el cual al salir y al volver y al regresar A se producen campos gravitatorios de escasa duración, en los cuales A cae libremente, mientras que B es contenido por fuerzas exteriores. De estos tres campos gravitatorios, el primero y el último no tienen influencia alguna en la marcha relativa de los relojes de A y de B, pues éstos se encuentran en el mismo sitio al salir y al regresar, y una diferencia de marcha en el campo gravitatorio no se verifica, según la fórmula [91], mas que cuando los dos relojes están separados por una distancia l. Pero prodúcese, si, una diferencia de marcha cuando B da la media vuelta. Si τ es el tiempo que dura la media vuelta, y durante el cual, considerando B como inmóvil, existe un campo gravitatorio, entonces el reloj A que se encuentra en el campo g y a la distancia l del reloj B, adelantará sobre éste en una cantidad que, según la fórmula [91] (pág. 364), es muy aproximadamente ${\tfrac {gl}{c^{2}}}\tau$. Pero en los tiempos del movimiento uniforme de A, a los cuales hay que aplicar el principio especial de la relatividad, ocurre lo contrario, esto es, que el reloj de A retrasa sobre el de B en la cantidad ${\tfrac {\beta ^{2}}{2}}t$. Por tanto, en total, al regreso, el reloj de A tiene sobre el de B un adelanto de

${\frac {gl}{c^{2}}}\tau -{\frac {\beta ^{2}}{2}}t$.

Ahora bien; afirmamos que este valor coincide exactamente con el resultado de la primera consideración, cuando A era tenido por inmóvil; esto es, que es igual ${\frac {\beta ^{2}}{2}}t$.

Pues como el observador en movimiento, al dar la media vuelta, pasa de la velocidad v a la velocidad -v, resulta su variación de velocidad, en conjunto, igual a 2v; su aceleración obtendráse dividiendo por el tiempo empleado τ, siendo, pues, $g={\tfrac {2v}{\tau }}$. Por otra parte, en el momento de dar la media vuelta, ha transcurrido ya la mitad del tiempo del viaje; la distancia de los dos observadores es, pues, entonces $l=v{\tfrac {t}{2}}$.

De aquí se infiere que $gl=v^{2}{\tfrac {t}{\tau }}$, y

${\frac {gl}{c^{2}}}\tau -{\frac {\beta ^{2}}{2}}t={\frac {v^{2}}{c^{2}}}t-{\frac {\beta ^{2}}{2}}t={\frac {\beta ^{2}}{2}}t$,

que era lo que se quería demostrar.

La paradoja de los relojes descansa, pues, en una falsa aplicación de la teoría especial de la relatividad, cuando es, en verdad, la general la que debe ser aplicada.

Igual error comete la objeción siguiente, que sigue siempre haciéndose, aun cuando es trivial su explicación.

Según la teoría general de la relatividad, un sistema de coordenadas que se halle en rotación respecto de las estrellas fijas, esto es, por ejemplo, un sistema fijo en la tierra, es igualmente lícito que el sistema en reposo con respecto a las estrellas fijas. En aquel sistema, empero, las estrellas fijas adquirirán enormes velocidades; si r es la distancia de una estrella, su velocidad será $v={\tfrac {2\pi r}{T}}$, siendo T la duración de un día. Esta velocidad será igual a la velocidad de la luz c, cuando sea $r={\tfrac {cT}{2\pi }}$; si se mide r con la unidad astronómica de longitud, que es el año de luz ^[1], habrá que dividir ésta por c · 365, si se pone T = 1 día. Así, pues, tan pronto como la distancia supere ${\tfrac {1}{2\pi \cdot 365}}$ años de luz, será la velocidad mayor que c. Ahora bien; las más próximas estrellas fijas están a distancias del Sol que valen varios años de luz; por otra parte, la teoría de la relatividad afirma (VI, 6, pág. 283) que la velocidad de los cuerpos materiales tiene que ser más pequeña siempre que la velocidad de la luz. Aquí parece patente la contradicción.

Pero ésta proviene solamente de que la proposición v < c está limitada a la teoría especial de la relatividad. En la general adopta la siguiente forma estricta: es posible siempre, como sabemos, elegir un sistema de referencia tal que en la inmediata vecindad de un punto universal cualquiera valga la geometría universal de Minkowski y sea, pues, la geometría euclidiana y no exista campo gravitatorio, y tengan las g₁₁....g₃₄ los valores de la fórmula [89] (pág. 352); con referencia a este sistema y en ese estrecho espacio es la velocidad de la luz c = 3 · 10¹⁰ centímetros/sec, el límite máximo de todas las velocidades.

Pero si esas condiciones no se cumplen; si existen campos gravitatorios, naturalmente toda velocidad, tanto la de cuerpos materiales como la de la luz, puede tener un valor numérico cualquiera. Pues las líneas luminosas en el universo hállanse determinadas por G = s² = 0, esto es, limitándonos al plano xt, por

$s^{2}=g_{11}x^{2}+2g_{14}xt+g_{44}t^{2}=0$;

de esta ecuación puede calcularse ${\tfrac {x}{t}}$, y ésta es la velocidad de la luz. Si, por ejemplo, g₁₄ = 0, se saca de g₁₁x² + g₄₄t² = 0 el valor ${\tfrac {x}{t}}={\sqrt {-{\tfrac {g_{44}}{g_{11}}}}}$ como velocidad de la luz, la cual dependerá del valor que tengan g₁₁ y g₄₄.

Si tomamos de sistema de referencia la Tierra, existe el campo centrífugo (III, 9, pág. 96) ${\tfrac {4\pi ^{2}r}{T^{2}}}$, que, en grandes distancias, adopta valores inmensos; las g tienen entonces también valores que se alejan mucho de los euclidianos (fórmula [89]). Por tanto, la velocidad de la luz, para algunas direcciones del rayo luminoso, resulta mucho mayor que su valor ordinario c, y otros cuerpos pueden igualmente alcanzar velocidades mucho mayores.

En un sistema cualquiera de coordenadas gaussianas, no sólo será otra la velocidad de la luz, sino que los rayos luminosos tampoco siguen siendo rectos. Sobre esta curvatura de los rayos luminosos se funda una segunda comprobación óptica del principio general de la relatividad. Las líneas universales de la luz son líneas geodésicas, lo mismo que las trayectorias de inercia de los cuerpos materiales, y, por tanto, cúrvanse en los campos gravitatorios, lo mismo que éstas; sólo que la desviación de la luz es mucho más pequeña a causa de su enorme velocidad.

Compréndese esta desviación, sin teoría alguna, por el principio de equivalencia; pues en un sistema de referencia acelerado, todo movimiento rectilíneo uniforme aparece como curvado y no uniforme; debe, pues, suceder otro tanto para un campo gravitatorio cualquiera.

fig133

Un rayo luminoso que, procedente de una estrella fija, pasa cerca del Sol es, pues, atraído por éste y recorre una trayectoria algo cóncava hacia el Sol (figura 133); el observador sobre la Tierra sitúa la estrella en la prolongación del rayo incidente, por lo cual le aparece algo desviada hacia fuera. Este fenómeno no puede observarse sino durante la breve duración de un eclipse de Sol, pues en otro momento los rayos solares hacen invisibles las estrellas fijas que se encuentran en su proximidad.

El último eclipse de Sol tuvo lugar el 29 de mayo de 1919; los ingleses organizaron dos expediciones con el exclusivo objeto de determinar si se verifica o no el «efecto de Einstein». Una de ellas fué a las costas occidentales de Africa, y la otra al norte del Brasil, y trajeron una serie de fotografías de las estrellas que rodean al Sol. El resultado de la medición de las placas pudo conocerse el 6 de noviembre de 1919 y significó el triunfo de la teoría de Einstein; la desviación predicha por Einstein, que debe ser junto al Sol de 1,7 segundos de arco, existe en su pleno valor.

Desde este resultado grandioso del profetismo moderno, puede considerarse la teoría de Einstein como una conquista definitiva de la ciencia.

Nadie puede decir con seguridad si será o no posible encontrar otros fenómenos observables que comprueben la teoría. Pero es verosímil que el arte de experimentar de los próximos años o siglos supere al nuestro como el nuestro supera a los trabajos del tiempo de Newton; de suerte que es lícito esperar que la nueva teoría se encuentre cada día más en concordancia con la experiencia.

11. Macrocosmos y microcosmos.

Ya hemos visto que la noción consecuente de las fuerzas de inercia como acciones recíprocas conduce necesariamente a aplicar la teoría al Cosmos entero. Trátase de comprender por qué el sistema de referencia, para el cual vale la métrica euclidiana en el espacio del sistema solar, está justamente en reposo (o en movimiento de traslación) relativamente a la totalidad de las masas cósmicas. Pero, además, la observación de más remotos sistemas estelares, de estrellas dobles, enseña que allí ocurre lo mismo. Parece, según esto, como que el campo métrico determinado por la totalidad de las masas tuviese por doquiera el mismo carácter, salvo cuando le sobrevienen perturbaciones locales por masas próximas.

Siempre han sido las especulaciones sobre el universo un tema preferido de los ingenios fantásticos; pero también la astronomía científica se ha ocupado de tales problemas. Sobre todo, se ha tratado mucho la cuestión de si los cuerpos celestes son en número finito o infinito, y ha habido que decidirse en pro de lo primero; sólo podemos aquí dar una leve indicación de los fundamentos en que se apoya tal solución. Si los astros se hallasen repartidos en el espacio con bastante uniformidad, y si su número fuese infinito, entonces el cielo entero debería resplandecer en clara luz, porque entonces habría siempre una estrella en cualquier dirección que se mirase; a no ser que la luz, en su camino hasta nosotros, fuese debilitada y finalmente absorbida. Pero puede afirmarse, fundándose en muy fuertes razones, que no hay absorción de la luz en el espacio cósmico. Por tanto, habrá que pensar la totalidad de las estrellas como una gigantesca aglomeración de astros que, o acaba de pronto, o, por lo menos, va poco a poco rarificándose de dentro a fuera.

Pero esta representación plantea una grave dificultad, si partimos de la mecánica de Newton. ¿Cómo permanecen las estrellas juntas? ¿Cómo es que no se pierden en la nada? Es sabido que todas las estrellas tienen velocidades considerables; pero están repartidas irregularmente en todas las direcciones, y no se observa indicio alguno de que el conjunto tienda a deshacerse.

A esto se contestará: «la gravitación recíproca mantiene juntas a las estrellas».

Pero esta respuesta es falsa. Hace tiempo que se conocen los métodos adecuados para resolver estos problemas. Son los métodos de la teoría cinética de los gases; un gas consta de innumerables moléculas, que se mueven confusamente unas respecto de las otras y son conocidas las leyes de estos movimientos.

Ahora bien; es claro que un gas que no se halla encerrado entre paredes sólidas se deshace al punto; la experiencia y la teoría coinciden en enseñar que un sistema de cuerpos no permanece continuamente en cohesión, aun cuando los cuerpos se atraigan por fuerzas que actúen, según la ley de Newton, en proporción inversa del cuadrado de la distancia.

El sistema de todos los cuerpos celestes debiera comportarse lo mismo que un gas, y no se comprende, por tanto, cómo es que no muestra tendencia alguna a perderse en el espacio cósmico infinito.

Einstein ha dado a esto una muy extraña respuesta: «Porque el universo no es infinito.» Bien; pero ¿dónde están sus límites? ¿No es absurdo admitir que el universo esté «rodeado de una tapia»?

Pero limitado y finito no son términos idénticos. Imagínese la superficie de una esfera; ésta es, sin duda, finita, y, sin embargo, no tiene límites. Einstein afirma que el espacio tridimensional es lo mismo; puede, en efecto, afirmarlo, pues la teoría general de la relatividad admite una curvatura del espacio. Y llega así a la teoría siguiente del universo: si se prescinde de la distribución no uniforme de los astros y se substituye ésta por una distribución uniforme de las masas, puede preguntarse cuándo podrá tal distribución mantenerse permanentemente en reposo, según las ecuaciones de los campos gravitatorios. La respuesta dice así: «La medida de curvatura del espacio tridimensional tiene que tener por doquiera un valor positivo constante, como lo tiene la de una superficie esférica de dos dimensiones.» Es evidente que sobre una superficie esférica un número finito de puntos de masa, apartándose unos de otros por su velocidad, extiéndense uniformemente y forman una especie de equilibrio dinámico. Exactamente esto mismo debe acontecer en la distribución tridimensional de los astros. Einstein llega incluso a apreciar la magnitud que tiene la «curvatura del universo», merced a una hipótesis plausible sobre la masa total de los astros; pero, por desgracia, esa curvatura se manifiesta tan pequeña ^[2], que no hay esperanza, por ahora, de comprobar empíricamente este audaz pensamiento.

Si, pues, la curvatura del universo tiene por doquiera el mismo valor, síguese entonces que el campo métrico tiene por doquiera el mismo carácter en el universo y que es euclidiano precisamente en aquel sistema de referencia que se halla en reposo en la totalidad de las masas (o se mueve con respecto a ellas con movimiento rectilíneo uniforme). Esta proposición contiene el núcleo de los hechos que Newton quería exponer por medio de su doctrina del espacio absoluto.

Todo intento de representarse este universo «esférico» finito, pero ilimitado, es naturalmente vano y tan imposible como el de conseguir una intuición de las curvaturas locales del universo en la proximidad de masas gravitantes. Y, sin embargo, tiene esta teoría consecuencias muy concretas. Imaginemos un telescopio en el observatorio de Babelsberg dirigido hacia una determinada estrella fija; al mismo tiempo, en los antípodas, por ejemplo, en la ciudad australiana de Sidney, hay otro telescopio dirigido exactamente al lugar del cielo que está enfrente. Cabe pensar, según la cosmología de Einstein, que los observadores de los dos telescopios estén viendo una y la misma estrella, que es recognoscible acaso por un espectro característico. En realidad, así como puede emprenderse un viaje alrededor del mundo tanto hacia el Este como hacia el Oeste, y realizarlo en ambas direcciones siguiendo uno y el mismo círculo máximo, así también un rayo luminoso, en el universo esférico de Einstein podrá salir de la estrella, seguir una línea geodésica en ambas direcciones y llegar a la Tierra en direcciones opuestas.

Hoy, estas consideraciones podrán quizá llamarse engendros de una fantasía desbocada; ¿quién sabe si dentro de pocos siglos no llegarán a ser hechos empíricos, merced a un arte refinadísimo de observación? Seria temerario negar tal posibilidad. Ya hoy hay astrónomos muy serios que parten de la teoría del macrocosmos dada por Einstein para sus exactas investigaciones sobre las leyes de la distribución de las estrellas fijas.

Mas también en el microcosmos, en el universo de los átomos, penetran las ideas de Einstein. Ya hemos tocado antes (V, 15, página 245) la cuestión de las notables fuerzas que impiden que un electrón o un átomo se deshaga. Ahora bien; éstos son aglomeraciones inauditas de energía en mínimos espacios; por tanto, han de ocultar en su seno enormes curvaturas de espacio o, dicho de otro modo, campos gravitatorios. Ofrécese el pensamiento de que éstos son los que mantienen juntos las cargas eléctricas que tienden a separarse.

Pero esta teoría se halla en sus comienzos y es dudoso si tendrá o no buen éxito. Por numerosas experiencias sabemos que en el mundo de los átomos imperan leyes nuevas, extrañas, en las cuales se expresa una armonía de números enteros que entendemos aún imperfectamente: la teoría llamada de los quanta, elaborada por Planck (1900). Aquí tiene la palabra la investigación futura.

12. Conclusión.

Ya conocemos, aunque sólo a grandes rasgos, la teoría del espacio y del tiempo establecida por Einstein. Hemos visto cómo se origina en las teorías físicas de sus predecesores, cómo un proceso claramente perceptible de objetivación y relativización conduce a través de las inextricables sendas de la ciencia hasta las más altas cumbres de la abstracción, que caracteriza hoy los conceptos fundamentales de las ciencias naturales exactas. La fuerza de la doctrina nueva viene de su origen experimental; es hija del experimento, y ha engendrado a su vez nuevos experimentos que testimonian su valor. Pero lo que constituye su trascendencia allende los estrechos límites de la investigación particular es la grandeza, la audacia, la rectitud de los pensamientos. La teoría de Einstein representa una tendencia espiritual cuyo ideal es un sano equilibrio entre la libre fantasía creadora, la lógica critica y la paciente sumisión a los hechos. No es una concepción del universo, si universo significa algo más que no sólo la multiplicidad espacio-tiempo de Minkowski; pero a quien se sume amorosamente en su riqueza ideal le da indicios y le abre camino hacia una concepción del universo. Pues aun fuera de la ciencia es la consideración objetiva y relativa de las cosas una gran adquisición, una liberación de prejuicios, un gran salto que da la vida por encima de normas cuya pretensión de valer en absoluto desvanécese ante el juicio critico del relativista.

---

1. Un año de luz es la distancia que recorre la luz en un año (365 días); la velocidad de la luz es de 300.000 kilómetros por segundo.
2. Según una estimación de De Sitter, el «contorno del universo», esto es, la longitud de una línea universal geodésica que vuelve sobre si misma, es de unos cien millones de años de luz.