La teoría de la relatividad de Einstein/II
LAS LEYES FUNDAMENTALES DE LA MECANICA CLASICA
1. Equilibrio y concepto de fuerza.
La mecánica ha tenido su punto de partida históricamente en la teoría del equilibrio o estática; lógicamente también es esta estructura la más natural.
El concepto fundamental de la estática es la fuerza; procede del sentimiento subjetivo del esfuerzo al realizar un trabajo corporal. De dos hombres, es el más fuerte el que puede levantar la piedra más pesada, tender el arco más recio. En esta medida de la fuerza, con que Ulises demuestra a los pretendientes su derecho, y que en los viejos cantares heroicos juega un papel importantísimo, hállase el germen de la objetivación del sentimiento subjetivo del esfuerzo. El paso inmediato fué la elección de una unidad de fuerza y la medición de todas las fuerzas con respecto a esa unidad; esto es, la relativización del concepto de fuerza. El peso, o sea la fuerza que tira hacia abajo todas las cosas terrestres, ofrecía una unidad de fuerza en forma comodísima: un trozo de metal que, por un acto de la autoridad política o sacerdotal, quedase determinado como unidad de peso. Hoy son Congresos internacionales los que establecen las unidades. Como unidad de peso, vale en la técnica el peso de un determinado trozo de platino que se conserva en París; esta unidad, llamada gramo (g.), es la que usaremos en lo sucesivo. El instrumento que sirve para comparar los pesos de diferentes cuerpos es la balanza.
Dos cuerpos son de igual peso cuando, puestos en ambos platillos de la balanza, no deshacen el equilibrio de ésta. Si en uno de los platillos de la balanza se colocan dos cuerpos de igual peso y en el otro platillo un cuerpo que mantenga el equilibrio con los otros dos, entonces este cuerpo tiene doble peso que uno de los otros dos. Procediendo sucesivamente de esta manera, nos proporcionamos, partiendo de la unidad, una manera de determinar cómodamente el peso de cada cuerpo.

No es nuestro objeto explicar aquí cómo por esos medios se hallan y se interpretan las sencillas leyes de la estática de cuerpos fijos, por ejemplo, las leyes de la palanca. Nos ocuparemos solamente de aquellos conceptos que sean indispensables para entender la teoría de la relatividad.
Al hombre primitivo, además de las fuerzas que residen en su propio cuerpo, o en el de sus animales domésticos, manifiéstanse otras fuerzas, sobre todo en los procesos que llamamos hoy elásticos. Entre ellos se encuentra la fuerza que requiere un arco, una ballesta, para ponerlos en tensión. Esa fuerza puede compararse fácilmente con pesos. Si se quiere, por ejemplo, medir la fuerza necesaria para tender un alambre en espiral hasta una longitud determinada (fig. 6), bastará determinar el peso que hace falta colgarle para que, con dicha longitud, se conserve el equilibrio; en este caso, la fuerza del resorte es igual al peso, sólo que el peso será para abajo y el resorte para arriba. En este proceder empléase tácitamente el principio de que la acción y la reacción en el equilibrio son iguales.
Si se perturba el equilibrio debilitando o aumentando una de las fuerzas, se produce movimiento. Un peso levantado en la mano cae al suelo si la mano que lo sujeta y que desarrolla la fuerza contraria, abandona el peso; sale volando la flecha cuando el arquero suelta la cuerda del arco en tensión. La fuerza crea movimiento. Este es el punto de partida de la dinámica, la cual investiga las leyes de este proceso.
2. Teoría del movimiento. Movimiento rectilíneo.
Primeramente es necesario someter a un análisis el concepto del movimiento mismo. La descripción exacta, matemática, del movimiento de un punto consiste en ir indicando, de momento en momento, el lugar en que se encuentra el punto con relación al sistema de coordenadas previamente elegido. El matemático utiliza para ello fórmulas. Queremos evitar esta manera, no fácil para todos, de exponer leyes y conexiones, y por eso vamos a emplear, en su lugar, un método gráfico de exposición, que explicaremos sobre un ejemplo sencillísimo: el movimiento de un punto en línea recta. Sobre la recta elegimos un punto-cero, la unidad de longitud será el centímetro, como es corriente en la física. El punto móvil en el momento de comenzar esta consideración, momento del tiempo que designamos con la indicación t = 0, hállase a la distancia x = 1 cm. del punto-cero; en 1 sec, el punto se ha corrido hacia la derecha en 1/2 cm.; de suerte que, para t = 1, la distancia al punto-cero tiene el valor de x = 1,5 cm.; en el segundo siguiente se corre el punto otro tanto, de suerte que x = 2 cm., y así sucesivamente. El cuadrito siguiente indica las distancias x correspondientes a los tiempos t:
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | . | . | . | . | . |
| x | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | . | . | . | . | . |
Vemos la misma conexión en las sucesivas rectas de la figura 7, en la cual el punto móvil está indicado por un circulito en la escala de las distancias. Ahora bien; en lugar de dibujar pequeñas figuras una sobre otra, puede disponerse una figura única, en la que x y t se presentan como coordenadas (figura 8); la cual tiene, además, la ventaja de que representa el lugar del punto, no sólo en cada segundo transcurrido, sino también en todos los tiempos intermedios; basta para ello unir por una curva las posiciones señaladas en la primera figura. En nuestro caso es manifiestamente una recta; porque el punto recorre en tiempos iguales distancias iguales, y, por tanto, las coordenadas x, t varían en igual proporción, y resulta así evidente que la imagen de esa ley es una recta. Llámase a este movimiento un movimiento uniforme. La velocidad, v, del movimiento se señala por medio de la relación o razón entre el camino recorrido y el tiempo transcurrido, o sea en signos:

En nuestro ejemplo, el punto recorre 1/2 cm. por segundo la velocidad es, pues, siempre la misma: 1/2 cm. por segundo.
La unidad de velocidad queda establecida ya por esta definición; es la velocidad en la cual el punto móvil recorre 1 cm. en 1 segundo. Dícese que es una unidad derivada, y se designa, sin la introducción de un nuevo valor, por el término cm., por sec. o cm./sec. Para expresar que las medidas de velocidad se reducen, según la fórmula [1], a medidas de longitud y de tiempo, dícese que la velocidad divide la dimensión longitud por el tiempo; esto es, . De modo correspondiente coordínase una determinada dimensión a toda magnitud que se construya con las magnitudes fundamentales: longitud l, tiempo t y peso G. Sabido esto, puede expresarse en seguida la unidad de la magnitud por las de longitud, de tiempo y de peso, cm., sec. y g.
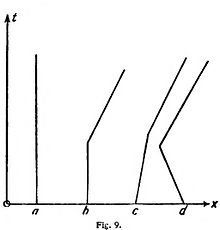
En las grandes velocidades, el camino x, recorrido en el tiempo t es grande; la recta que lo expresa en la figura correrá casi paralela al eje de las x; cuanto más pequeña sea la velocidad, tanto más se acercará la recta a la posición perpendicular al eje de las x. Un punto inmóvil tiene una velocidad igual a cero, y en nuestro diagrama será representado por una recta paralela al eje de las t, pues los puntos de esta recta tienen el mismo valor de x para todos los tiempos t (fig. 9, letra a).
Si un punto empieza estando inmóvil y luego de pronto, en un momento, recibe cierta velocidad y se mueve con esa velocidad, obtenemos la imagen de una quebrada, cuya parte primera es vertical (fig. 9, letra b). Si el punto se mueve primero hacia la derecha o hacia la izquierda con movimiento uniforme, y de pronto varia su velocidad, obtendremos igualmente líneas quebradas ({{#fig9|fig. 9]], letras c, d).
Si la velocidad anterior a la súbita variación es v1 (por ejemplo = 3 cm./sec.) y luego es v2 (por ejemplo = 5 cm./sec), entonces el aumento de la velocidad es v2 - v1 (es decir = 5-3 = 2 cm./sec). Si v2 es más pequeño que v1 (por ejemplo = 1 centímetro/sec), entonces v2 - v1 es negativo (a saber = 1 - 3 = -2 cm./sec.), y ello significa manifiestamente que el punto móvil de pronto retrasa su marcha.
Si un punto experimenta muchas variaciones sucesivas y momentáneas de velocidad, la representación de su movimiento será una linea muy quebrada o poligonal (fig. 10).

Si las variaciones de velocidad se siguen unas a otras con creciente rapidez y son, además, lo suficientemente pequeñas, pronto la línea poligonal llega a no distinguirse de una curva, que representa entonces un movimiento cuya velocidad varia continuamente y que, por tanto, no es uniforme, sino acelerado o retrasado (fig. 11).
Una medida exacta de la velocidad y su variación, la aceleración, no puede lograrse, en este caso, sino por los métodos del cálculo infinitesimal; bastará para nosotros que nos representemos la curva continua como un polígono cuyos lados rectos expresan movimientos uniformes con determinada velocidad. Supongamos que los vértices del polígono, esto es, las súbitas variaciones de velocidad, se siguen a intervalos de tiempo iguales; por ejemplo, . Si además son todos iguales, llámase el movimiento «uniformemente acelerado»; supongamos que cada variación de velocidad tiene la magnitud w, y que se verifican n en el segundo; será, pues, la total variación de velocidad para cada segundo (fig. 12):
Esta cantidad es la medida de la aceleración; su dimensión es manifiestamente , y su unidad es aquella aceleración en la cual, en la unidad de tiempo, la velocidad aumenta una unidad, o sea, refiriéndonos al sistema físico de medidas: cm./sec.2.

Si se quiere saber cuánto recorre un punto móvil, en movimiento uniformemente acelerado, durante un tiempo cualquiera t, represéntese el tiempo t dividido en n partes iguales (se entiende un tiempo cualquiera y no, como antes, un segundo dividido en n partes) y al término de cada espacio de tiempo sea dado al punto un súbito aumento de velocidad w; éste está en conexión con la aceleración b por la fórmula [2], si se substtituye el pequeño intervalo de tiempo t por ; tenemos, pues,
- Entonces la velocidad es:
Tras el primer espacio de tiempo Tras el segundo ídem id Tras el tercero ídem id , etc.
- El punto recorre:
Tras el primer espacio de tiempo, hasta Tras el segundo ídem id. id. Tras el tercero ídem id. id. , etc.
Tras el enésimo espacio de tiempo, esto es, al término del tiempo t, habrá llegado el punto a
pero
La suma de los números desde 1 hasta n puede calcularse simplemente sumando el primero y el último, el segundo y el penúltimo, etc.; resulta siempre n + 1 y hay de estas sumas. Si luego se substituye w por , se obtiene:
o sea:
Esto significa que las distancias recorridas en tiempos iguales son como los cuadrados de los tiempos. Si, por ejemplo, la aceleración b vale 10 m./sec, el punto recorrerá en el primer segundo 5 m.; en el segundo segundo, m.; en el tercer segundo, m., etc. Esta relación se representa por una línea curva en el plano xt, curva que se llama parábola (fig. 13). Si se compara esta figura con la figura 12, se ve cómo la linea poligonal representa aproximativamente la parábola de curvación constante; en ambas figuras se ha elegido la aceleración b=10, y ésta determina el aspecto de la curva, siendo inesenciales las unidades de longitud y de tiempo.

El concepto de aceleración puede aplicarse también a movimientos no uniformemente acelerados, tomando, en lugar de 1 sec, un tiempo tan breve de observación que, durante el mismo, el movimiento pueda considerarse como uniformemente acelerado. En este caso es la aceleración misma la que continuamente varia.
Todas estas definiciones son estrictas, y al mismo tiempo cómodas de obtener, cuando se estudia exactamente el proceso de subdivisión en pequeños trozos, para los cuales la cantidad considerada puede valer como constante; llégase entonces al concepto de valor límite, que constituye el punto de partida del cálculo diferencial. Históricamente fué, en efecto, la teoría del movimiento el problema para cuya solución descubrió Newton el cálculo diferencial y su inversa, el cálculo integral.
La teoría del movimiento—cinemática, foronomía—es la preparación para la mecánica propiamente dicha de las fuerzas, o sea la dinámica; es manifiestamente una especie de geometría del movimiento. En realidad, nuestras exposiciones gráficas representan cada movimiento como una formación geométrica en el plano, con las coordenadas x, t. Y en esto se trata de algo más que de una simple comparación; justamente en la teoría de la relatividad llega a tener una significación de principio la introducción del tiempo como coordenada junto a las medidas de espacio.
3. Movimiento en el plano.
Si queremos estudiar ahora el movimiento de un punto en un plano, bastará trasladar nuestro procedimiento de exposición. Se toma en el plano un sistema de coordenadas x, y, y se levanta perpendicularmente a él el eje de las t (fig. 14). Entonces, a un movimiento rectilíneo y uniforme en el plano xy corresponde una linea recta en el espacio xyt; pues si se proyectan en el plano xy los puntos de la recta que corresponden a las señales del tiempo t = 0, 1, 2, 3......, se advierte que la variación de lugar se verifica en linea recta y en intervalos uniformes.
Todo movimiento que no es rectilíneo y uniforme llámase acelerado; por, ejemplo, cuando una trayectoria curva es recorrida con velocidad constante; en este caso no varía la magnitud, pero sí la dirección de la velocidad. Un movimiento acelerado es representado en el espacio xyt por una curva cualquiera (fig. 15); la proyección de esa curva sobre el plano xy es la trayectoria plana. Compútase la velocidad y la aceleración pensando, en lugar de la curva, una línea poligonal inscrita en la curva y lo más pegada posible a ella; en cada vértice del polígono varia, no sólo la cantidad de la velocidad, sino también su dirección. Un análisis exacto del concepto de aceleración nos llevaría demasiado lejos; bastará decir que lo mejor es proyectar el punto móvil sobre los ejes coordenados x é y, y perseguir el movimiento rectilíneo de esos dos puntos proyectados, o, lo que es lo mismo, la variación temporal de las coordenadas x é y. Puede aplicarse entonces aquí la definición de la aceleración que dimos antes para los movimientos rectilíneos, y los dos componentes de aceleración que de ese modo se obtienen determinan el estado de aceleración del punto en movimiento. Es éste, como la velocidad, una magnitud dirigida.

4. Movimiento circular.
Sólo un caso vamos a considerar con algún detalle: el movimiento de un punto en una trayectoria circular con velocidad constante (fig. 16). Según lo dicho más arriba, es éste un movimiento acelerado, puesto que la dirección de la velocidad cambia continuamente. Si el movimiento no fuera acelerado, el punto móvil iría desde A en línea recta hacia adelante, con la velocidad v. Pero, en realidad, el punto debe permanecer en el círculo; tiene, pues, que experimentar un aumento de velocidad o aceleración, dirigida al centro M; llámase aceleración centrípeta. Ella es causa de que la velocidad en un punto próximo B, al que llega el móvil tras breve tiempo t, tenga otra dirección que la que tenia en el punto A. Ahora, en una figura lateral (fig. 16) dibujemos las velocidades en lo puntos A y B, partiendo de un punto cualquiera C, según su

dirección y cantidad; la cantidad v es la misma, pues el circulo ha de ser recorrido con velocidad constante; pero la dirección es diferente. Unamos los puntos extremos D y E de las dos flechas representativas de las velocidades; resultará que la distancia D E será manifiestamente el aumento de velocidad w que el segundo estado de velocidad recibe. Obtenemos así un triángulo isósceles C E D, cuya base es w y los lados v, y reconocemos en seguida que el ángulo α del vértice C es igual al ángulo A M B, correspondiente al arco de circulo A B recorrido por el punto en movimiento; pues las velocidades en A y en B son perpendiculares a los radios M A y M B, y forman, por tanto, el mismo ángulo. Por consiguiente, son semejantes los triángulos M A B y C D E, y se obtiene la proporción:
Ahora bien; , y, además, M A es igual al radio r y A B es igual al arco s con un pequeño error, que, eligiendo un pequeñísimo intervalo de tiempo t, puede reducirse cuanto se quiera.
Obtiénese, pues:
Dividamos por t' y observemos que
de donde resulta:
es decir: la aceleración centrípeta es igual al cuadrado de la velocidad de revolución dividido por el radio del círculo.
Sobre esta proporción descansa, como veremos, una de las primeras y más importantes demostraciones experimentales de la teoría newtoniana de la gravedad.
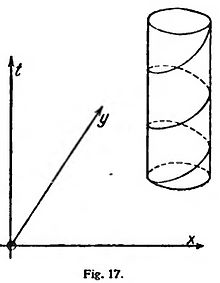
Acaso no sea superfino manifestar claramente cuál es el aspecto que el movimiento circular uniforme presenta en la exposición gráfica, como curva en el espacio xyt. Esta curva se produce manifiestamente haciendo que el punto móvil suba paralelamente al eje t y uniformemente, mientras se verifica el movimiento circular; obtiénese, pues, una línea helicoidal, o sea en forma de tornillo, que representa integramente la trayectoria y el curso temporal del movimiento. En la figura 17 está señalada en la superficie de un cilindro que tiene por base la trayectoria circular en el plano x y.
5. Movimiento en el espacio.
Para los movimientos en el espacio no sirve nuestra exposición gráfica, pues tenemos ya tres coordenadas para el espacio, x, y, z; y el tiempo t tendría que añadirse como cuarta coordenada. Por desgracia, nuestras facultades intuitivas limítanse al espacio tridimensional. Tiene que intervenir, pues, aquí el lenguaje matemático de las fórmulas; en efecto, los métodos de la geometría analítica permiten tratar por mero cálculo las propiedades y relaciones de las formaciones geométricas, sin que sea necesario acudir a la intuición ni dibujar figuras. Es más: este método es mucho más poderoso que la construcción. Principalmente, porque no está atenido a las tres dimensiones, sino que es aplicable a espacios de cuatro o más dimensiones. En el idioma de los matemáticos no significa el concepto de un espacio de más de tres dimensiones ningún objeto místico, sino que es simplemente una expresión abreviada para indicar que tenemos que habérnoslas con cosas que pueden determinarse íntegramente por más de tres datos numéricos. Así, la posición de un punto, en un determinado tiempo, ha de establecerse por medio de cuatro datos numéricos: las tres coordenadas espaciales x, y, z y el tiempo t. Si hemos aprendido ya a manejar el espacio xyt como imagen de movimientos planos, no nos será difícil considerar también los movimientos en el espacio tridimensional, con la imagen de curvas en el espacio xyzt. Esta concepción de la cinemática, como geometría en un espacio de cuatro dimensiones xyzt, tiene la ventaja de poder trasladar a la teoría del movimiento las conocidas leyes geométricas. Pero tiene, además, un sentido más profundo, que se ha de manifestar claramente en la teoría de Einstein. Se demostrará que los conceptos de espacio y tiempo, que son contenidos intuitivos de muy diferente cualidad, no pueden, como objetos de mediciones físicas, separarse uno de otro. Si la física quiere atenerse al principio fundamental de no admitir como real mas que lo físicamente determinable, tendrá que reunir los conceptos de espacio y tiempo en una unidad superior, que será precisamente el espacio cuatridimensional xyzt. Minkowski (1908) ha llamado a ese espacio el universo, queriendo manifestar así que el elemento de toda ordenación de las cosas reales no es el lugar y no es tampoco el momento, sino el suceso o el punto universal; es decir, un lugar en un tiempo determinado. La curva de un punto en movimiento la llamó curva universal, expresión que iremos usando en lo sucesivo. El movimiento rectilíneo uniforme corresponde, pues, a una recta universal; el movimiento acelerado, a una curva.
6. Dinámica. La ley de inercia.
Después de estas preparaciones, volvamos a la cuestión de donde hemos partido, a saber: ¿de qué manera producen las fuerzas movimientos?
El caso más sencillo es cuando no existe ninguna fuerza. Entonces un cuerpo inmóvil no entra seguramente en movimiento. Ya los antiguos hicieron esta determinación; pero creían, además, que la inversa era también cierta: donde hay movimiento tienen que actuar fuerzas que lo mantengan. Esta concepción trae en seguida dificultades; basta reflexionar sobre el por qué una piedra o un dardo lanzado a lo lejos sigue moviéndose cuando ha abandonado la mano que lo lanzó; esta mano es evidentemente la que lo puso en movimiento; pero su acción termina tan pronto como el movimiento comienza. Los pensadores de la antigüedad discurrieron mil maneras de explicar cuáles sean las fuerzas que mantienen a la piedra en movimiento. Pero Galileo fué el primero que descubrió el punto de vista exacto; advirtió que era un prejuicio admitir que dondequiera que hay movimiento tiene que haber también siempre fuerza. Más bien hay que preguntar qué propiedad cuantitativa del movimiento se halla en una conexión legal con la fuerza, si el lugar del cuerpo movido, o su velocidad, o su aceleración, o una magnitud combinada independiente de éstas. De este problema no es posible encontrar la solución por mera reflexión filosófica; hay que interrogar a la naturaleza, y la respuesta primera que ésta da, nos dice que las fuerzas tienen influencia sobre las variaciones de velocidad; pero que para la conservación de un movimiento, sin que varíen en nada la cantidad y dirección de la velocidad, no hace falta ninguna fuerza, y recíprocamente: si no hay fuerzas, permanece inalterada la cantidad y dirección de la velocidad; esto es: que un cuerpo en reposo permanece en reposo, y un cuerpo en movimiento rectilíneo uniforme permanece en movimiento rectilíneo uniforme.
Esta ley de la facultad de permanecer, o ley de la inercia, no se manifiesta, empero, tan claramente como su sencilla expresión verbal lo haría sospechar. Pues en nuestra experiencia no conocemos ningún cuerpo que esté realmente libre de toda acción, y si nos lo representamos en nuestra imaginación, surcando solitario en linea recta el espacio cósmico con velocidad constante, caemos al punto en el problema de la trayectoria absolutamente recta en el espacio absolutamente inmóvil, problema del que más tarde habremos de hablar detenidamente. Por eso, provisionalmente, entenderemos la ley de inercia en el sentido limitado que tenía para Galileo.
Nos representaremos una mesa lisa y perfectamente horizontal; sobre la mesa, una bola lisa también. El peso de la bola hace que ésta oprima la mesa; pero determinamos que no nos hace falta ninguna fuerza notable para mover la bola sobre la mesa muy lentamente. Sobre la bola no actúa evidentemente ninguna fuerza en dirección horizontal, pues de otro modo no permanecería en reposo por si misma. Démosle ahora a la bola una cierta velocidad; rodará en línea recto, y cada vez más despacio; pero este alentamiento es muy pequeño, y Galileo lo reconoció como un efecto secundario, que es de atribuir al roce con la mesa y con el aire, aun cuando las fuerzas actuantes en ese roce no puedan manifestarse por los métodos estáticos de que hemos partido. La visión exacta que distingue lo esencial, en un proceso, de los efectos laterales perturbadores, constituye precisamente el gran investigador.
Sobre la mesa confírmase, pues, en todo caso, la ley de inercia; queda establecido que, en ausencia de toda fuerza, la velocidad permanece constante en dirección y cantidad.
Por consiguiente, las fuerzas se relacionan con la variación de velocidad, con la aceleración. ¿Cómo? Sólo la experiencia puede decidirlo.
7. El choque o impulsión.
La aceleración de un movimiento no uniforme ha sido representada como el caso límite de súbitas variaciones de velocidad, en movimientos cortos uniformes. Por tanto, preguntaremos primero cómo una variación súbita de velocidad se produce por la entrada en acción de una fuerza. La fuerza tiene que actuar para ello tan sólo un breve instante; es lo que se llama un choque o impulsión La consecuencia de tal choque no depende solamente de la cantidad de la fuerza, sino también de la duración de su acción, aunque ésta sea muy breve. Defínese, pues, la cantidad de un choque de la manera siguiente:
Sean n impulsiones J, cada una de las cuales consiste en que, durante el tiempo de , actúa la fuerza K: si esas impulsiones se siguen rápidamente unas a otras, de manera que no haya pausas notables, la consecuencia será la misma que si la fuerza K se mantiene activa durante el segundo entero. Tendremos:
o bien:

Para representarse esto intuitivamente, piénsese, por ejemplo, una palanca de brazos iguales y un peso sobre una de las extremidades de la palanca. Sobre la otra extremidad, con un martillo, se dan golpes de igual fuerza y muy rápidos, de manera que la palanca permanezca en equilibrio (fig. 18). Es evidente que los golpes pueden ser más débiles y, en cambio, más frecuentes; o menos frecuentes y, en cambio, más fuertes; pero, en todo caso, la fuerza del choque J, multiplicada por el número n de choques, o dividida por el tiempo t que transcurre en cada choque, ha de ser siempre igual al peso K. Con esta «balanza de los choques» estamos en disposición de medir la fuerza de los mismos, aun cuando no podemos determinar la duración y la fuerza de cada uno; bastará determinar la fuerza K que hace equilibrio a n choques iguales en un segundo—hasta llegar a imperceptibles temblores de la balanza—y entonces la cantidad de cada choque será la enésima parte de K.
La dimensión del choque es y su unidad en el sistema usual de medida es sec. g.
8. La ley de la impulsión.
Consideremos nuevamente la bola sobre la mesa y estudiemos el efecto de los choques sobre ella. Para ello haremos uso de un martillo que pueda girar alrededor de un eje horizontal; dejaremos caer el martillo desde una altura determinada. Lo primero que haremos será estimar la fuerza del choque para cada altura de donde caiga el martillo. Luego le dejaremos caer sobre la bola que está inmóvil en la mesa: observemos la velocidad que recibe la bola por medio del choque, midiendo los centímetros que recorre en un segundo (fig. 19). El resultado es sencillísimo:
Cuanto más fuerte sea el choque, mayor es la velocidad, y a un choque doble corresponde una velocidad doble también; a un choque triple, una velocidad triple, y así sucesivamente. La velocidad y el choque hállanse en proporción constante; son proporcionales.

Esta es la ley fundamental de la dinámica, la ley de la impulsión, para el caso sencillo de que un cuerpo pase del reposo al movimiento. Si la bola tiene ya una velocidad, el choque la aumentará o la disminuirá, según alcance a la bola por detrás o por delante. Un fuerte contrachoque puede muy bien invertir súbitamente el movimiento de la bola.
La ley de la impulsión dice asi: las variaciones súbitas de velocidad del cuerpo son como los choques que las producen. Las velocidades, según su dirección, se calculan como positivas o negativas.
9. La masa.
Hasta ahora hemos operado solamente con una bola; ahora vamos a hacer el mismo experimento del choque con bolas de distinta especie; por ejemplo, de diferente tamaño o de distinta materia, unas macizas y otras huecas. Todas estas bolas vamos a ponerlas en movimiento por medio de choques de igual fuerza. El experimento demuestra que reciben entonces muy diferentes velocidades, y en seguida se ve que las bolas ligeras son muy aceleradas, mientras que las pesadas se mueven lentamente. Hallamos, pues, aquí una conexión con el peso, de la que más tarde hablaremos detenidamente, pues es uno de los fundamentos empíricos de la teoría general de la relatividad. Pero aquí vamos, por el contrario, a comprender esto claramente; a saber: que, en puro concepto, el hecho de que diferentes bolas, recibiendo todas choques de igual fuerza, adquieran diferentes velocidades, no tiene nada que ver con el peso. El peso actúa hacia abajo y produce la presión de la bola sobre la mesa, mas no una fuerza horizontal. Encontramos tan sólo que una bola resiste más al choque que otra; si la primera es también la más pesada, es éste un hecho empírico nuevo; pero, desde el punto de vista adoptado aquí, no puede en modo alguno deducirse del concepto de peso. Lo que nosotros comprobamos es una diferente resistencia de las bolas a los choques; llámase resistencia de inercia, y se mide por la relación entre el choque J y la velocidad producida v. Para designar esta relación se ha elegido la palabra masa y la letra m; se establece, pues, que
y esta fórmula indica que, para el mismo cuerpo, un aumento de la impulsión J produce una mayor velocidad; de suerte que la relación tiene siempre el mismo valor m. Según esta definición de la masa, ya su unidad no es de libre elección, porque las unidades de velocidad y de impulsión han sido ya determinadas; por eso la masa tiene la dimensión
y su unidad en el sistema de medidas usual es: sec.2 g./cm.
En el uso corriente del lenguaje, significa la palabra masa lo mismo que cantidad de substancia, de materia, sin que estos conceptos mismos estén bien definidos; el concepto de substancia figura, como categoría del entendimiento, entre los inmediatamente dados. Pero en la física—y esto hay que subrayarlo—no tiene la voz masa otra significación que la dada por la fórmula [5]: es la medida de la resistencia a variaciones de velocidad.
Podemos ahora escribir la ley de la impulsión, con más generalidad, del siguiente modo:
Esta fórmula determina la variación w de velocidad que un cuerpo en movimiento experimenta por el choque J.
Suele interpretarse la fórmula también de esta manera:
La fuerza dada de la impulsión J del martillo es comunicada a la bola movible; el martillo «pierde» la impulsión J y ésta reaparece en el movimiento de la bola en igual cantidad mw. La bola en movimiento lleva consigo esa fuerza de impulsión, y cuando ella a su vez choca contra un cuerpo, le da una impulsión J' = mw', donde w' es la disminución de su velocidad; en cierto modo, transmite nuevamente su impulsión. La impulsión total de todos los cuerpos participantes es siempre la misma; háblase, pues, de la ley de conservación de la impulsión.
10. Fuerza y aceleración.
Antes de seguir estudiando el notable paralelismo de masa y peso, vamos a trasladar las leyes que hemos descubierto al caso de fuerzas en actuación continua. Desde luego, una estricta fundamentación de las proposiciones sobre esta materia no puede hacerse sino por los métodos del cálculo infinitesimal; sin embargo, las siguientes consideraciones pueden, por lo menos, proporcionar una representación aproximada de las conexiones.
Una fuerza en actuación continua produce un movimiento con velocidad que de continuo varia. Pensemos ahora, en lugar de esa fuerza continua, una sucesión rapidísima de choques; la velocidad, a cada choque, experimenta una pequeña variación súbita; puede representarse por una línea universal muy quebrada, como en la figura 10; y esa línea quebrada inscríbese en la verdadera línea universal, que es una curva uniforme, pudiendo substituirla para el cálculo. Pues bien; si n choques durante un segundo substituyen a la fuerza K, tendrá cada uno de ellos, según la fórmula [4], el valor
donde t es el breve tiempo que transcurre en un choque. En cada choque verificase una variación de velocidad w, la cual, según la fórmula [6], está determinada por
Ahora bien; según la fórmula [2], tenemos que
Se obtiene, pues:
Esta es la ley del movimiento de la dinámica para fuerzas de actuación continua. Expresada en palabras, dice así:

Una fuerza produce una aceleración proporcional a ella; la relación constante K: b es la masa.
En esta forma vale la ley primeramente sólo para movimientos que se verifican en línea recta, y en los cuales la fuerza actúa en esa misma recta. Si tal no es el caso, si la fuerza actúa lateralmente a la dirección momentánea del movimiento, entonces hay que generalizar algo la ley. Represéntese el lector la fuerza dibujada como una flecha, y ésta proyectada en tres direcciones perpendiculares unas a otras; por ejemplo, los ejes coordenados. En la figura 20 está representado el caso de que la fuerza actúe en el plano xy, y están sus proyecciones sobre el eje x y el eje y. Piénsese igualmente el punto en movimiento proyectado sobre los ejes; cada uno de los puntos de proyección realiza sobre su eje un movimiento. Entonces la ley del movimiento dice que las aceleraciones de esos movimientos proyectados están con los correspondientes componentes de fuerza en la relación mb=K. Pero no insistiremos en estas generalizaciones matemáticas, que no nos ofrecen ningún concepto nuevo.
11. Ejemplo. Vibraciones elásticas.
Como ejemplo de la relación entre fuerza, masa, aceleración, consideraremos un cuerpo que bajo la actuación de fuerzas elásticas puede vibrar. Tomemos, v. gr., un resorte de acero que sea recto y ancho, y lo afianzamos en una de sus extremidades, de manera que, estando en reposo, el canto estrecho se halle en posición horizontal. Al otro extremo lleva el resorte una bola (figura 21). El resorte puede oscilar en el plano horizontal; la gravedad no tiene influjo alguno en su movimiento, el cual depende solamente de la fuerza elástica del resorte. Si se le empuja con poca fuerza, la bola se mueve casi en linea recta; sea la dirección de su movimiento el eje de las x.
Si se pone la bola en movimiento, realizará una oscilación periódica, cuya esencia se comprende de la siguiente manera: Con la mano apártese la bola un poco de la posición de equilibrio; al hacerlo se sentirá la fuerza retroactiva del resorte. Si se suelta la bola, esa fuerza le comunica una aceleración y la bola vuelve con creciente velocidad a la posición media. Al suceder esto, la fuerza retroactiva, esto es, también la aceleración, disminuye de continuo y al paso de la posición media se hace igual a cero; pues en esta posición media la bola está en equilibrio y no actúa sobre ella ninguna fuerza aceleradora. En el mismo punto en donde la velocidad es máxima, es mínima la aceleración. A consecuencia de la facultad de conservación, pasa la bola por la posición de equilibrio, y entonces la fuerza del resorte actúa retrasando y frena el movimiento. Cuando la primitiva oscilación ha llegado al otro extremo, la velocidad queda rebajada a cero y la fuerza alcanza su valor máximo; al mismo tiempo la aceleración tiene también su máximo valor, ya que en ese momento invierte la dirección de la velocidad. A partir de aquí, el proceso se repite en sentido inverso.

Si ahora se substituye la bola por otra de diferente masa, se ve que el carácter del movimiento permanece idéntico; pero varia la duración de la oscilación. Cuanto mayor sea la masa, más lento será el movimiento y más pequeña la aceleración; si la masa disminuye, aumentará el número de oscilaciones.
En muchos casos puede admitirse que la fuerza retroactiva K es exactamente proporcional a la oscilación x. En tal caso puede representarse en intuición geométrica el curso del movimiento de la manera siguiente: Sea un punto P, móvil en la periferia de un circulo de radio a; el punto P se mueve con movimiento uniforme a razón de ν veces en un segundo. Recorre, pues, el circulo 2πa (π=3,14....) en el tiempo sec; es decir, que su velocidad es
De aquí se infiere que la velocidad de A es
Ahora bien; la proyección del punto P en el eje de las y realiza un movimiento pendular exactamente igual. Cuando P recorre la distancia s, B recorre el trocito η y puede escribirse también, como se escribió para ξ
A esta variación η, de y corresponde una variación de la velocidad v=2πνy del punto A cuyo valor es
y, por lo tanto, una aceleración de A

Midiendo la fuerza K necesaria para una oscilación y contando las oscilaciones, puede determinarse la masa m del péndulo.
La imagen que presenta la línea universal de tal oscilación es, evidentemente, una linea ondulada en el plano xt, siendo x la dirección de la oscilación (fig. 23). En el dibujo se ha admitido que la bola, en el momento t = 0, pasa la posición media x=0 hacia la derecha. Se ve que siempre, al pasar por el eje t, es decir, cuando x=0, la dirección de la curva es la de acercarse mucho al eje x, por donde se manifiesta la máxima velocidad; en cambio, la curva es allí muy recta, es decir, que la variación de velocidad o aceleración es nula. Lo contrario sucede en los sitios que corresponden a las extremidades de la oscilación.
12. Peso y masa.
Ya al introducir el concepto de masa hemos notado que la masa y el peso tienen un evidente paralelismo; los cuerpos pesados opónense a las fuerzas aceleradoras más que los cuerpos ligeros. ¿Es ésta una ley exacta? Lo es, en efecto. Para exponer claramente la situación, consideremos nuevamente el experimento que consiste en poner en movimiento por medio de choques unas bolas sobre una mesa lisa y horizontal. Tomemos dos bolas, A y B, teniendo B doble peso que A esto es, que B en la balanza hace equilibrio a dos ejemplares de A. Ahora les damos a A y a B iguales impulsiones sobre la mesa y observamos la velocidad alcanzada; encontramos que A se mueve con doble velocidad que B.
La bola B, que pesa doble que la bola A, opone a la variación de velocidad una resistencia doble que la que opone la bola A. Esto puede también expresarse diciendo: cuerpos que tienen masa doble tienen peso doble, o, en general: las masas, m, son como los pesos, G. La relación entre el peso y la masa es un número perfectamente determinado; señálase con g y se escribe:

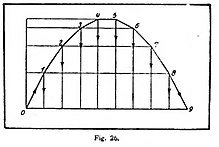
Naturalmente, el experimento que hemos hecho para explicar la ley es en extremo grosero [1]. Hay otros muchos fenómenos que demuestran el mismo hecho, sobre todo éste: que todos los cuerpos caen igualmente de prisa. En esto hay que suponer, naturalmente, que sobre el movimiento no influyan más fuerzas que la gravedad; hay que hacer la experiencia, por tanto, en el espacio vacío, para evitar la resistencia del aire. Apropiado para la demostración es un plano inclinado (fig. 24), sobre el cual se dejan rodar dos bolas exteriormente iguales, pero de diferente peso; obsérvase que llegan abajo exactamente al mismo tiempo.
El peso es la fuerza que empuja; la masa determina la resistencia; si están en razón directa, resultará que un cuerpo más pesado será empujado con más fuerza que uno más ligero; pero, en cambio, opondrá al impulso mayor resistencia, y el resultado final será que el cuerpo pesado y el cuerpo ligero rodarán o caerán con igual velocidad. Ello se desprende también de nuestras fórmulas; pues si en la fórmula [7] se pone, en lugar de la fuerza, el peso G, y se admite ésta, según la fórmula [9], como proporcional a la masa, se obtendrá:
esto es:
Todos los cuerpos tienen, pues, verticalmente hacia abajo la misma aceleración, cuando se mueven influidos exclusivamente por el peso, ya caigan libremente o sean lanzados. La cantidad g, la aceleración de la gravedad, tiene el valor g = 981 cm./sec2.

Los experimentos más precisos para comprobar esta ley se realizan por medio de péndulos; ya Newton observó que las duraciones de las oscilaciones para una longitud l del péndulo son siempre iguales, sea cual fuere la bola que pende del hilo. El proceso de oscilación es el mismo que hemos descrito más arriba, al tratar del péndulo elástico; pero aqui la bola es empujada, no ya por un resorte de acero, sino por la gravedad. La fuerza de la gravedad debe pensarse dividida en dos componentes: uno actúa en la longitud del hilo y lo tiende; el otro actúa en la dirección del movimiento, y es la fuerza que empuja la bola.
La figura 25 muestra la bola del péndulo en la oscilación x; se ven dos triángulos rectángulos semejantes, cuyos lados, por tanto, tienen la misma relación:
y por lo tanto,
esto es, que la relación entre el peso y la masa es para ambos péndulos la misma. La hemos llamado g en la fórmula [9]; obtenemos, pues, la ecuación
Por donde se ve que g puede determinarse por medio de la longitud del péndulo y del número de oscilaciones.
Muchas veces se expresa la ley de la proporcionalidad del peso a la masa de la siguiente manera:
Se entiende por masa pesada simplemente el peso dividido por g; y a la masa propiamente dicha añádese el adjetivo «inerte», para distinguirla de la anterior.
Ya Newton sabía que esta ley vale exactamente. Hoy está comprobada por las más exactas mediciones que la física conoce; fueron éstas llevadas a cabo por Eoetvoes (1890). Es, pues, totalmente legítimo emplear las pesadas en la balanza, no sólo para comparar los pesos, sino también las masas.
Debería pensarse que una ley como ésta había de estar firmemente arraigada en los fundamentos de la mecánica. Sin embargo, no es el caso, como demuestra nuestra exposición que reproduce con bastante fidelidad el contenido de la mecánica clásica. Más bien diríase que está pegada, como una especie de curiosidad, al nexo de las demás proposiciones. Muchos pensadores se han asombrado de ello, pero nadie buscó tras este hecho una conexión más profunda. Hay muchas diferentes fuerzas que pueden impulsar una masa; ¿por qué no ha de haber una que sea proporcional a la masa? Una pregunta, a la que no se espera contestación, permanece incontestada. Y así permaneció la cosa intacta durante siglos. Ello fué posible, porque los éxitos de la mecánica de Galileo y de Newton fueron extraordinarios; dominó esta mecánica, no sólo los procesos del movimiento terrestre, sino también los de los astros, y se manifestó como seguro fundamento de toda la ciencia exacta de la naturaleza. Particularmente hacia la mitad del siglo xix propúsose la investigación interpretar todos los procesos físicos como procesos mecánicos en el sentido de la teoría de Newton. Y durante la construcción del edificio olvidáronse de inquirir si los cimientos eran bastante sólidos para sostener el conjunto. El primero que ha reconocido la importancia de la ley que establece la igualdad entre la masa inerte y la masa pesada, y su significación para los fundamentos de las ciencias físicas, ha sido EINSTElN.
13. La mecánica analítica.
El problema de la mecánica calculativa o analítica consiste en partir de la fórmula del movimiento:
y hallar el movimiento cuando son dadas las fuerzas K. La fórmula misma no da sino la aceleración; esto es, la variación de velocidad. Sacar de aquí la velocidad y de ésta, a su vez, el lugar variable del punto en movimiento es un problema del cálculo integral que puede ser muy difícil, cuando la fuerza varía por modo muy complicado en lugar y en tiempo. Nos dará un concepto de la naturaleza del problema nuestra deducción de la variación de lugar en un movimiento uniformemente acelerado en una línea recta (pág. 37). Más complicado es ya el movimiento en un plano bajo la acción de una fuerza constante de dirección determinada, como en un movimiento de caída o de lanzamiento. También aquí podemos substituir aproximadamente el curso constante por una serie de movimientos uniformes que, por impulsiones sucesivas, se producen unos a otros. Representémonos de nuevo nuestra mesa y establezcamos que la bola debe recibir a cada brevísimo tiempo t, un choque de la misma cantidad y dirección (fig. 26). Si la bola parte del punto o con una velocidad inicial cualquiera, llegará en t sec. a un punto 1, en donde le alcanza el primer choque; de aquí corre en otra dirección con otra velocidad, durante t sec, hasta que en el punto 2 recibe un nuevo choque que la desvía, etc. Cada una de las desviaciones es determinable por la ley de impulsión; por lo tanto, puede construirse todo el proceso del movimiento y se ve que el punto de partida, la dirección inicial y la velocidad inicial determinan enteramente el posterior curso. En este movimiento de retroceso tenemos una imagen grosera del movimiento de una bola sobre un plano inclinado; y la imagen coincidirá tanto mejor con el proceso, en realidad continuo, cuanto más pequeño sea el intervalo de tiempo que se haya elegido entre los choques.
Lo que aquí se ha conseguido por construcción lo realiza el cálculo integral en el caso de fuerzas continuamente activas. También aquí permanecen enteramente arbitrarios el punto de partida y la velocidad inicial en cantidad y dirección; pero si éstos son dados, queda perfectamente determinado el ulterior curso del movimiento. Una y la misma ley de fuerza puede, pues, producir infinitos movimientos, según la elección de las condiciones iniciales; así, la inmensa muchedumbre de los movimientos de caída y de proyección dependen todos de una y la misma ley de fuerza, la gravedad, que actúa verticalmente hacia abajo.
Generalmente no se trata en los problemas mecánicos del movimiento de un cuerpo, sino de varios que ejercen acciones unos sobre otros; entonces no están dadas las fuerzas mismas, sino que éstas dependen a su vez del movimiento desconocido. Se comprende que el problema de determinar por cálculo los movimientos de varios cuerpos ha de ser sumamente complicado.
14. La ley de la energía.
Pero hay una ley que resume y facilita grandemente el problema, y que en la posterior evolución de las ciencias físicas ha adquirido una gran importancia. Es la ley de la conservación de la energía. No podemos, naturalmente, manifestarla aquí en toda su generalidad; ni siquiera demostrarla; vamos tan sólo a conocer su contenido por algunos ejemplos sencillos.
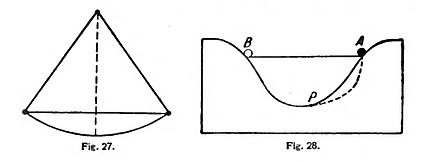
Un péndulo, que se deja caer, estando la bola a cierta altura, pasa por la posición media y asciende del otro lado a la misma altura—con un pequeño error ocasionado por frotamiento y resistencia del aire (fig. 27)—. Si en vez de la trayectoria circular se pone otra, colocando la bola sobre rieles, por ejemplo, como en las montañas rusas (fig. 28), ocurre exactamente lo mismo: la bola sube siempre a la misma altura de que salió.
De aquí se deriva fácilmente que la velocidad que la bola tiene en un punto P cualquiera de su trayectoria depende sólo de la profundidad a que se halle el punto P bajo el punto de partida A. Para comprenderlo bien represéntese cambiado el trozo AP de la trayectoria y conservado intacto el resto PB. Si la bola, recorriendo una de las dos trayectorias de A a P, llegase a P con otra velocidad inicial que recorriendo la otra trayectoria, entonces al seguir rodando de P a B no alcanzarla en ambos casos justamente B' como término; pues para ello es evidentemente necesario que la velocidad inicial en P esté unívocamente determinada. Por consiguiente, la velocidad en P no depende de la forma del trozo de trayectoria recorrido; y como P es un punto cualquiera, tiene esto una validez general. La velocidad v tiene, pues, que estar determinada exclusivamente por la altura de la caída h. La exactitud de esta ley proviene de que la trayectoria—el riel— como tal no opone ninguna resistencia al movimiento, no ejerce ninguna fuerza sobre la bola en la dirección del movimiento, sino que sólo recoge la presión perpendicular de la bola. Si falta el riel, tenemos la calda libre o el lanzamiento, y todo sigue igual: la velocidad en cada punto depende sólo de la altura de la caída.

Este hecho no sólo se comprueba experimentalmente, sino que se deriva también de nuestras leyes del movimiento; al hacerlo se obtiene además una forma de la ley que regula la dependencia en que la velocidad está de la altura de la caída.
Afirmamos que dice así: Sea x la trayectoria contada positivamente hacia arriba (figura 29); sea v la velocidad, m la masa, G el peso del cuerpo. Pues bien, la cantidad
conserva el mismo valor durante todo el proceso de la caída.
Para demostrarlo, pensemos primeramente que E es una cantidad cualquiera que depende del movimiento y varia de momento en momento. En un pequeño espacio de tiempo t, la cantidad E varia en e; entonces habremos de decir que la relación es la velocidad de variación de E, y al hacerlo, desde luego pensamos que el espacio de tiempo t debe tomarse siempre lo más pequeño posible—como antes hicimos al definir la velocidad v y la aceleración b—. Si la cantidad E no cambia en el tiempo, es naturalmente su velocidad de variación cero, e inversamente. Ahora vamos a calcular la variación de la expresión anterior E en el tiempo t; durante este tiempo la altura de la caída x disminuye de vt y la velocidad v aumenta de w= bt. Por lo cual E una vez transcurrido el tiempo t, tendrá el valor de
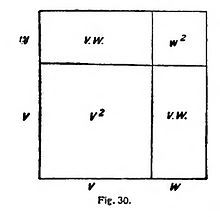
Pero sabemos que
lo cual quiere decir que el cuadrado levantado sobre las dos distancias sucesivas v y w puede dividirse en un cuadrado cuyo lado sea v, en otro cuyo lado sea w y en dos rectángulos iguales cuyos lados sean v y w (figura 30).
Por donde resulta:
Si se substrae ahora el antiguo valor de E, tendremos como variación
Y entonces la velocidad de la variación se expresa
Aquí puede prescindirse del sumando que contiene t, puesto que disminuyendo el espacio de tiempo, puede llegar a ser tan pequeño como se quiera. Se obtiene, finalmente, para expresión de la velocidad de variación:
Esta expresión, empero, tiene un valor igual a cero, según las leyes de la mecánica, pues, según la fórmula [10], mb = mg = G, Queda, pues, demostrado que la cantidad E de la fórmula [12] permanece invariable con el tiempo. Si se dan el punto de partida y la velocidad inicial del movimiento, esto es, los valores de x y v para t = 0, entonces recibe la expresión E, según la fórmula [12], un valor determinado, que conserva luego durante el movimiento.
De aquí se infiere que cuando el cuerpo sube, es decir, cuando x aumenta, tiene v que disminuir, e inversamente. Cada uno de los dos miembros o sumandos de la expresión E no puede crecer sino a costa del otro. El primero es característico del estado de velocidad del cuerpo; el segundo, de la altura que tiene que subir contra la gravedad. Hay nombres especiales para ellos.
Su suma:
La dimensión de cada cantidad de energía es [E] = [Gl], y su unidad g. cm.
El nombre de capacidad de trabajo procede, naturalmente, del trabajo que el cuerpo humano realiza al levantar un peso. Según la ley de la energía, ese trabajo transfórmase al caer en energía cinética. Si, por el contrario, se le da a un cuerpo energía cinética, lanzándolo a alguna altura, transfórmase ésta en energía potencial o capacidad de trabajo.
Exactamente lo mismo que hemos desarrollado aquí para el movimiento de caída vale, en amplia extensión, para sistemas de muchos cuerpos, con tal de que se cumplan dos condiciones:
- 1. ª No deben producirse acciones del exterior; el sistema debe estar cerrado en sí mismo.
- 2. ª No deben manifestarse procesos en los cuales la energía mecánica se transforme en calor, en fuerza de tensión eléctrica, en afinidad química, etc.
En tal caso, vale siempre la proposición, que dice que
y de ella depende la energía cinética de las velocidades y la energía potencial de la posición de los cuerpos en movimiento.
En la mecánica de los astros realízase con máxima pureza ese caso ideal; aquí vale la dinámica ideal, cuyos principios hemos desenvuelto.
Pero en el mundo terrestre no ocurre lo mismo. Todo movimiento está sometido a frotación, por donde su energía se traduce en calor. Las máquinas con las cuales producimos movimiento no hacen sino transformar fuerzas térmicas, químicas, eléctricas, magnéticas. No puede, pues, mantenerse la ley de la energía en la estrecha forma mecánica. Pero puede mantenerse en forma generalizada. Si llamamos Q a la energía térmica, C a la química, W a la electromagnética, podrá decirse que, para sistemas cerrados, la suma
es constante.
Muy lejos nos llevaría el estudiar cómo fué descubierto y fundado este hecho por Robert Mayer, Joule (1842) y Helmholtz (1847), o investigar cómo las formas no mecánicas de la energía son determinadas cuantitativamente. Pero más tarde emplearemos el concepto de energía, cuando hablemos de la profunda conexión que la teoría de la relatividad ha descubierto entre masa y energía.
15. Unidades dinámicas de fuerza y masa.
El método con que hemos deducido las leyes fundamentales de la mecánica limita su validez en cierta manera a la superficie de nuestra mesa y su inmediata vecindad. Pues hemos abstraído nuestros conceptos y leyes de experiencias en espacios pequeños, de experimentos de laboratorio. La ventaja de este método ha sido que no hemos necesitado hacer reflexiones sobre los supuestos que se refieren al tiempo y al espacio; los movimientos rectilíneos de que trata la ley de inercia pueden trazarse sobre la mesa con un tiralíneas, y tenemos a nuestra disposición aparatos y relojes para medir las trayectorias y los movimientos.
Pero ahora va a tratarse de salir de la habitación para sumirnos en el espacio cósmico. El primer paso para ello es un «viaje alrededor del mundo»; por tal entiende el uso común del idioma la pequeña esfera terrestre. Nos propondremos el problema siguiente: ¿valen todas las leyes establecidas lo mismo en un laboratorio de Buenos Aires o del Cabo que aquí?
En efecto valen, salvo una excepción, a saber: la cantidad de la aceleración de la gravedad g. Hemos visto que ésta puede medirse muy exactamente por medio de observaciones del péndulo. Pero se ha puesto de manifiesto que uno y el mismo péndulo oscila en el ecuador algo más lentamente que en las comarcas del Norte o del Sur; en un día, es decir, en una revolución de la Tierra, verifícanse en el ecuador menos oscilaciones. Esta diminución es muy regular hasta los polos, en donde g tiene su máximo valor. Más tarde veremos la causa de este fenómeno; por ahora, basta con su comprobación. Pero el hecho tiene muy incómodas consecuencias para el sistema de medidas con que nosotros hemos medido hasta ahora las fuerzas y las masas.
Mientras no hacemos mas que comparar pesos con la balanza de palanca, no hay dificultad. Pero figurémonos una balanza de resorte igualada con pesos; si se traslada a comarcas más al Sur o más al Norte, se encontrará que, cargada con los mismos pesos, da distintas oscilaciones. Por tanto, si se identifica, como hasta ahora hemos hecho, el peso con la fuerza, no queda otro recurso que afirmar: la fuerza del resorte se ha alterado y depende de la latitud geográfica. Mas evidentemente no es éste el caso; no se ha alterado la fuerza del resorte, sino la fuerza de la gravedad; es, pues, falso tomar como unidad de fuerza el peso de un cuerpo determinado en todos los lugares de la Tierra. Pero se puede elegir como unidad de fuerza el peso de un cuerpo determinado en un lugar determinado de la Tierra; éste puede luego, cuando la aceleración de la pesantez g sea conocida por mediciones pendulares, trasladarse a otros lugares. Así procede realmente la técnica; su medida de la fuerza es el peso de un cuerpo normal determinado que está en París: el gramo. Lo hemos usado siempre hasta ahora, sin tener en cuenta su variabilidad según el lugar; pero en las mediciones exactas hay que hacer la reducción al lugar normal (París).
La ciencia ha abandonado este sistema de medidas, en el cual un lugar del globo es privilegiado, y ha adoptado otro menos caprichoso.
Un método apropiado para ello nos ofrece la ley fundamental de la mecánica misma. En lugar de referir la masa a la fuerza, determínase la masa como cantidad fundamental de la dimensión independiente [m] y se elige caprichosamente su unidad: un determinado trozo de metal tiene la masa 1. De hecho se toma para ello el mismo trozo de metal que le sirve de unidad de peso a la técnica, el gramo de París, y esta unidad de masa se llama también gramo (g.). La doble significación de esta palabra, como unidad de peso en la técnica y como unidad de masa en la física, puede fácilmente inducir a errores. Nosotros empleamos en lo que sigue el sistema de medidas de la física, cuyas unidades fundamentales son: para longitud, el centímetro (cm.); para tiempo, el segundo (sec.), y para masa, el gramo (g.).
La fuerza tiene ahora la siguiente dimensión derivada
y la unidad es g. cm./sec. 2, que también se llama una dina.
El peso defínese por G=mg; la unidad de masa tiene, pues, el peso G=g dinas; es variable según la latitud geográfica, y en nuestras latitudes tiene el valor g=981 dinas. Esta es la unidad técnica de fuerza. La fuerza de una balanza de resorte es, expresada en dinas, naturalmente constante, pues su capacidad de acelerar una masa determinada es independiente de la latitud geográfica.
La dimensión de la impulsión es ahora
su unidad es g. cm./sec. Por último, la dimensión de la energía es:
y su unidad es g. cm2/sec.2, o sea dina-centímetro.
Ahora que ya hemos librado nuestro sistema de medidas de todas las impurezas terrestres, podemos entrar en el estudio de la mecánica de los astros.
- ↑ Así, por ejemplo, se desprecia la circunstancia de que para producir la rotación de la bola en movimiento hay que vencer una resistencia que procede de la distribución de las masas en el interior de la bola (momento de inercia).

![{\displaystyle [v]=[{\frac {l}{t}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38d88095b67999bbf05cb9a9c7bb9d70ef974cd3)


![{\displaystyle [b]=\left[{\tfrac {v}{t}}\right]=\left[{\tfrac {l}{t^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00cb60119a1b0851d42b4d8223b1b26598dc9c51)





























![{\displaystyle [J]=[tG]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edd678d8c92ab497a00412864efc75c1f53bb472)

![{\displaystyle [m]=[{\frac {t^{2}G}{l}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f486372aae76ac980100d9e636981c11d9f5e280)









































![{\displaystyle [K]=[mb]=[{\frac {ml}{t^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2e9ad95f55c3c1a1a0c9ce801d1eb4673e64fe)
![{\displaystyle [J]=[tK]=[{\frac {ml}{t}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7840cf4873c0e588558c9effcc54869297b0e3e9)
![{\displaystyle [E]=[m^{2}v^{2}]=[{\frac {ml^{2}}{t^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268a014176d3386cf0135beaa5ac5990b8598c0d)