La teoría de la relatividad de Einstein/V

--—

V

LAS LEYES FUNDAMENTALES DE LA ELECTRODINAMICA

1. La electrostática y la magnetostática.

Ya sabian los antiguos que un cierto mineral, la piedra imán, atrae el hierro, y que al ámbar frotado (en griego, electrón) adhiérense los ligeros corpúsculos. Pero las ciencias del magnetismo y la electricidad son hijas de la época contemporánea, que había aprendido en la escuela de Galileo y Newton a hacerle a la naturaleza preguntas racionales y a discernir su respuesta en el experimento.

Los hechos fundamentales de los fenómenos eléctricos fueron establecidos hacia el año 1600; vamos a enumerarlos rápidamente. Como medio para la producción de efectos eléctricos, servia entonces exclusivamente el frotamiento. Gray descubrió (1729) que algunos metales puestos en contacto con cuerpos electrizados por frotamiento reciben iguales propiedades que éstos; demostró que las acciones eléctricas pueden ser conducidas en los metales. Llegóse así a la división de las substancias en conductores y no conductores (aisladores). Du Fay (1730) descubrió que la acción eléctrica no es siempre atracción, sino que también puede ser repulsión; interpretó este hecho admitiendo dos flúidos que hoy llamamos electricidad positiva y negativa, y estableció que dos cuerpos cargados con electricidad del mismo nombre se repelen, y que si están cargados con electricidad de nombre distinto se atraen.

Vamos a definir, desde luego, el concepto de carga eléctrica cuantitativamente; al hacerlo no nos atendremos estrictamente a los pensamientos, a veces muy sinuosos, que históricamente han conducido al establecimiento de los conceptos y leyes, sino que elegiremos un orden de definiciones y experimentos en el cual la conexión lógica aparezca con la mayor posible claridad.

Representémonos un cuerpo M electrizado por frotamiento; este cuerpo actúa por atracción o repulsión sobre otros cuerpos electrizados. Para estudiar este efecto vamos a tomar pequeños corpúsculos de prueba; por ejemplo, esferas cuyo diámetro es muy pequeño respecto de la próxima distancia del cuerpo M, en donde queremos investigar la fuerza. Pongamos uno de esos corpúsculos de prueba, P, en las proximidades del cuerpo M, cuya acción queremos estudiar; P experimenta una fuerza estática de determinada cantidad y dirección que puede medirse con los métodos de la mecánica; por ejemplo, por medio de contrapesos, merced a palancas o hilos.

Ahora tomemos dos de esos corpúsculos de prueba, frotados en diferente manera, P₁ y P₂, y pongámoslos sucesivamente en el mismo lugar en las proximidades de M, y midamos en los dos casos las fuerzas K₁ y K₂ en cantidad y dirección. Al hacerlo convenimos que en adelante fuerzas de dirección opuesta las consideraremos como de la misma dirección, pero calculando su cantidad con signos contrarios.

El experimento da por resultado que las dos fuerzas tienen la misma dirección; pero su cantidad puede ser diferente y tener diferente signo.

Ahora coloquemos los dos corpúsculos de prueba en otro lugar en las proximidades de M y midamos nuevamente las fuerzas K'₁ y K'₂ en cantidad y dirección; encontraremos nuevamente que las dos tienen la misma dirección; pero, en general, diferentes cantidades y signos diferentes.

Si establecemos ahora la relación K₁:K₂ entre las fuerzas en el primer lugar, y luego la relación K'₁:K'₂ entre las fuerzas en el segundo lugar, se verá que ambas relaciones tienen el mismo valor, que puede ser positivo o negativo:

${\frac {K_{1}}{K_{2}}}={\frac {K'_{1}}{K'_{2}}}$

De este resultado puede concluirse:

1.º La dirección de la fuerza ejercida por un cuerpo electrizado Msobre un corpúsculo de prueba P no depende de la naturaleza y electrización del corpúsculo de prueba, sino sólo de las propiedades del cuerpo M.

2.° La relación de las fuerzas sobre dos corpúsculos de prueba, colocados sucesivamente en el mismo lugar, es independiente de la elección del lugar; esto es, de la posición, naturaleza y electrización del cuerpo M. Depende sólo de las propiedades del corpúsculo de prueba.

Se elige ahora, como corpúsculo unidad, un corpúsculo de prueba determinado y electrizado por modo determinado, y se le atribuye la carga o cantidad de electricidad +1. Con éste se mide siempre la fuerza que el cuerpo M ejerce; sea designada esta fuerza con la letra E. Entonces ésta determina también la dirección de la fuerza K ejercida sobre cualquier otro cuerpo de prueba P. La relación de las cantidades K:E depende solamente del cuerpo de prueba P y se llama su carga eléctrica, e; ésta puede ser positiva o negativa, según que K y E sean, en estricto sentido, de igual dirección o de dirección contraria. Puede escribirse, pues:

${\frac {K}{E}}=e$ ó $K=eE$[40]

La fuerza E sobre la carga 1 llámase también fuerza del campo eléctrico del cuerpo M; una vez fijada la unidad de carga, depende solamente de la naturaleza eléctrica del cuerpo M; determina su acción eléctrica en el espacio circundante o, como se dice, su campo eléctrico.

Por lo que se refiere a la carga unidad, seria prácticamente imposible establecerla por medio de un precepto acerca de la electrización de un determinado cuerpo de prueba; se buscará más bien para ella una definición mecánica. Se consigue del siguiente modo:

Lo primero es cargar con igual fuerza dos cuerpos de prueba; el criterio de igual carga es que los dos cuerpos de prueba puestos en el mismo sitio sufran igual fuerza del tercer cuerpo M. Entonces los dos cuerpos de prueba se repelerán mutuamente con igual fuerza; decimos que su carga es 1 cuando esta repulsión es igual a la unidad de fuerza, habiéndose puesto los dos cuerpos a una distancia uno de otro igual a la unidad de longitud. Al operar así no hemos supuesto nada acerca de la dependencia entre la fuerza y la distancia.

Por estas definiciones, ya es la cantidad de electricidad o carga eléctrica una cantidad mensurable como longitudes, masas o fuerzas.

La ley más importante sobre las cantidades de electricidad fué expresada al mismo tiempo por {Watson y Franklin (1747), y es que en todo proceso electrizador siempre se producen iguales cantidades de electricidad positiva y negativa. Si se frota, por ejemplo, una barra de cristal con un paño de seda, queda el cristal electrizado positivamente; en el paño de seda se halla exactamente la misma carga negativa.

Este hecho de experiencia puede interpretarse así: que el frotamiento no produce, sino que separa las dos especies de electricidad. Represéntanse como dos flúidos que existen en todos los cuerpos en igual cantidad. En los cuerpos no electrizados, «neutrales», están en igual cantidad en todos los puntos; de suerte que su acción hacia afuera se anula. En los cuerpos electrizados, empero, están separados; una parte de la electricidad positiva ha pasado, por ejemplo, de un cuerpo a otro, y otra tanta negativa en dirección opuesta.

Pero es evidente que basta admitir un solo flúido, que puede fluir independientemente de la materia; entonces a la materia que esté libre de tal flúido hay que atribuirle una determinada carga, la positiva, por ejemplo, y al flúido la opuesta, la negativa. La electrización consiste entonces en que el flúido negativo pasa de un cuerpo a otro; el primero será entonces positivo, porque la carga positiva de la materia ya no está compensada, y el segundo será negativo, porque tendrá un exceso de flúido negativo.

La discusión entre los partidarios de las dos hipótesis, la teoría de uno y dos flúidos, duró mucho tiempo y permaneció infructuosa e inútil hasta que el descubrimiento de nuevos hechos le puso término. No entraremos en el detalle de estas discusiones, y diremos, en breves palabras, que, finalmente, halláronse diferencias características en la conducta de ambas electricidades, las cuales indicaban que la electricidad positiva está firmemente adherida a la materia, mientras que la negativa es libremente móvil. Esta teoría rige aún hoy; seguiremos este tema luego, al hablar de la teoría de los electrones.

Otra discusión se planteó acerca de cómo las fuerzas eléctricas de atracción y repulsión son transmitidas por el espacio. Los primeros decenios de la indagación eléctrica no estaban aún dominados por la influencia que luego hubo de ejercer la teoría newtoniana de la atracción; una acción a distancia parecía impensable, y regían proposiciones metafísicas, como que la materia sólo puede actuar donde está; y así se inventaron diferentes hipótesis para explicar las fuerzas eléctricas: emanaciones que salen de los cuerpos cargados, y al llegar a otro cuerpo hacen presión, y otras suposiciones por el estilo. Pero cuando la teoría de la gravitación de Newton hubo conquistado la victoria, acabó por hacerse habitual la representación de una fuerza actuante inmediatamente en la lejanía. Pues, efectivamente, sólo se trata de un hábito mental, cuando una representación se imprime tan honda en los cerebros, que es usada como postrer principio explicativo. Sin duda, no transcurre mucho tiempo entonces sin que la especulación metafísica, vestida muchas veces con el ropaje de filosofía crítica, dé la prueba de que el principio de explicación usado es necesario al pensamiento y que su contrario es irrepresentable; pero la ciencia empírica progresiva no suele, afortunadamente, curarse de ello, y si nuevos hechos lo exigen, acude a las representaciones condenadas. La evolución de la teoría de las fuerzas eléctricas y magnéticas es un ejemplo de esa marcha circular de las teorías; al principio es una teoría de acción próxima, fundada en motivos metafísicos; luego ésta es deshecha por una teoría de acción a distancia, según el modelo de Newton; y, por último, se transforma, obligada por nuevos hechos descubiertos, en una teoría general de la acción próxima. Estas oscilaciones no son, empero, signos de debilidad; pues las imágenes que con las teorías se conexionan no son lo esencial; lo esencial son los hechos empíricos y sus conexiones conceptuales. Y si se siguen éstos, no se ve ninguna oscilación, sino una constante evolución llena de fuerza lógica interior. Los primeros ensayos teóricos anteriores a Newton pueden bien considerarse como fuera de la serie, porque los hechos eran conocidos harto mal para poder dar puntos firmes de asiento a las teorías. Pero la teoría de la acción a distancia que surgió luego, según el modelo de la mecánica de Newton, está perfectamente fundada en la esencia de los hechos eléctricos. Una investigación que disponía de los medios experimentales del siglo xviii tenía necesariamente que fundarse en las observaciones entonces posibles, y, por tanto, venir a la conclusión de que las fuerzas eléctricas y magnéticas actúan, del mismo modo que la gravitación, en la lejanía. Aun hoy, desde el punto de vista de la muy desarrollada teoría de la acción próxima de Faraday y Maxwell, es perfectamente lícito exponer la electroestática y la magnetoestática por medio de fuerzas a distancia, y tal exposición conduce, si se emplea inteligentemente, siempre a resultados exactos.

El pensamiento de que las fuerzas eléctricas actúan en la lejanía, como la gravitación, fué concebido primeramente por Aepinus (1759); éste llegó incluso a concebir la gravitación y la electricidad como efectos del mismo flúido. Representóse, en el sentido de la teoría de un solo flúido, que una materia sin flúido eléctrico repelería otra materia; pero que siempre hay un pequeño exceso de flúido que produce la atracción de la gravitación. No consiguió establecer—y es extraño que no lo consiguiera—la ley exacta de la dependencia entre las acciones eléctricas y la distancia; pero pudo explicar cualitativamente el fenómeno de la influencia. Este consiste en que un cuerpo cargado actúa por atracción, no sólo sobre otros cuerpos cargados, sino también sobre cuerpos no cargados, particularmente sobre conductores; la carga del mismo nombre, en efecto, es empujada al lado del cuerpo influenciado que mira hacia el cuerpo actuante y la del otro nombre al lado opuesto, por lo cual supera la atracción a la repulsión (fig. 76).

fig76

La verdadera ley fué descubierta por Priestley, el descubridor del oxígeno (1767), y lo fué por un camino ingenioso, indirecto, cuya fuerza demostrativa es, en el fondo, más grande que la de la medición directa. Independientemente de aquél, Cavendish derivó la ley de la misma manera (1771). Pero el nombre que recibe es el del investigador que primero la demostró, por medición directa de las fuerzas, Coulomb (1785).

Según ella, la fuerza que ejercen uno sobre otro dos cuerpos con las cargas e₁ y e₂, a la distancia r, es:

$K={\frac {e_{1}e_{2}}{r^{2}}}$, [41]

suponiendo que los máximos diámetros de los cuerpos sean pequeños respecto de la distancia. Esta limitación expresa que la ley, lo mismo que la de la gravitación, es una ley elemental idealizada; para concluir, por medio de ella, a la actuación de cuerpos de extensión limitada, hay que representarse la electricidad, que hay en ellos, como dividida en pequeñas partes y calcular las acciones de las partículas de un cuerpo sobre las del otro, dos a dos, y sumarlas.

Por la fórmula [41] queda establecida la dimensión de la cantidad de electricidad, pues para la repulsión de dos cargas iguales rige

${\frac {e^{2}}{r^{2}}}=K$; esto es: $e=r{\sqrt {K}}$;

y, por tanto:

$[e]=[l{\sqrt {K}}]=\left[l{\sqrt {\frac {ml}{t^{2}}}}\right]=\left[{\frac {l}{t}}{\sqrt {ml}}\right]$.

Así, la unidad de carga en el sistema c, g, s queda determinada; hay que escribirla:

${\frac {{\text{cm.}}{\sqrt {\text{g. cm.}}}}{\text{sec.}}}$.

La fuerza E eléctrica del campo, definida por K = eE, tiene la dimensión

$[E]=\left[{\frac {K}{e}}\right]=\left[{\frac {K}{l{\sqrt {K}}}}\right]=\left[{\frac {\sqrt {K}}{l}}\right]=\left[{\frac {\sqrt {ml}}{lt}}\right]=\left[{\frac {1}{t}}{\frac {\sqrt {m}}{l}}\right]$,

y su unidad es:

${\frac {1}{\text{sec.}}}{\sqrt {\frac {\text{g}}{\text{cm.}}}}$.

Desde el establecimiento de la ley de Coulomb, la electroestática se hizo ciencia matemática. El problema más importante es, dada la cantidad total de electricidad en cuerpos conductores, calcular la distribución de las cargas en éstos, bajo la acción de la influencia recíproca, y las fuerzas que de aquí se originan. El desarrollo de este problema matemático es interesante, porque muy pronto se apartó de la primitiva formulación, como teoría de acción a distancia, y se transformó en una pseudoacción próxima; es decir, que, en lugar de las sumas de las fuerzas de Coulomb, se ponen ecuaciones diferenciales, en donde como incógnita entra la fuerza del campo, E, o una cantidad en conexión con ésta, el potencial. Pero no podemos seguir de cerca estas cuestiones puramente matemáticas, en las que se han distinguido notablemente Laplace (1782), Poisson (1813), Green (1828) y Gauss (1840). Sólo nos fijaremos en un punto. En este tratamiento de la electroestática, llamado generalmente teoría del potencial, no se trata propiamente de ninguna teoría de la acción próxima en el sentido que hemos dado a la palabra anteriormente (IV, 6, pág. 125); pues las ecuaciones diferenciales refiérense a la variación topográfica de las fuerzas del campo de lugar en lugar; pero no contienen ningún miembro que exprese una variación temporal. Por lo cual no condicionan una propagación de la fuerza eléctrica con velocidad finita, sino que, a pesar de la forma diferencial, exponen una acción momentánea a distancia.

La teoría del magnetismo se desenvolvió de igual manera que la electroestática. Podemos, pues, abreviar. La diferencia esencial entre las dos esferas de fenómenos es que hay cuerpos que conducen la electricidad, mientras que el magnetismo está adherido con la materia y no se mueve sino con ésta.

Un cuerpo alargado y magnetizado, una aguja magnética, tiene dos polos, esto es, dos lugares de los cuales parece salir la fuerza magnética; rige la ley de que dos polos de igual nombre se repelen y dos de nombre distinto se atraen. Si se parte la aguja magnética, los dos trozos no quedan magnetizados contrariamente, sino que cada trozo adquiere en el punto de rotura un nuevo polo y se torna en una aguja magnética completa con dos polos iguales. Y esto sucede en todos los trozos en que se divida la aguja, por pequeños que sean.

fig77

Se ha inferido de aquí que existen, sin duda, dos clases de magnetismo, como en la electricidad; pero que estas dos clases no pueden moverse libremente, sino que se presentan en las mínimas partes de la materia, en las moléculas, en igual cantidad cada una, pero separadas. Cada molécula es pues, una pequeña aguja magnética con sus polos Norte y Sur (fig. 77); la magnetización de un cuerpo finito consiste en que todos los magnetos o imanes elementales, que estaban antes en pleno desorden, se colocan paralelamente. Entonces compénsanse los efectos de los polos sucesivos Norte (+) y Sur (—), hasta los dos extremos de la serie, en las superficies extremas del cuerpo, y todo el efecto parece salir de ellos.

Tomando una aguja magnética muy larga y fina, puede conseguirse que en la proximidad de un polo sea ya imperceptible la fuerza del otro. Por lo cual cabe aquí también operar con corpúsculos de prueba, a saber: con agujas magnéticas muy largas y finas; con éstas pueden verificarse todas las mediciones de que hemos hablado en la electricidad. Se llega a la definición de la cantidad magnética o fuerza polar p y a la de la fuerza del campo magnético H. La fuerza magnética que un polo p experimenta en el campo h es:

$K=Ph$. [42]

La unidad del polo se elige de manera que dos polos unidad, a la distancia 1, ejerzan la fuerza repulsiva 1. La ley por la cual varía la fuerza de dos polos p₁ y p₂ con la distancia, hallóla también Coulomb por medición directa; dice, como la ley de atracción de Newton:

$K={\frac {p_{1}p_{2}}{r^{2}}}$. [43]

Evidentemente, las dimensiones de las cantidades magnéticas son iguales a las correspondientes eléctricas, y sus unidades tienen los mismos signos en el sistema c, g, s.

La teoría matemática del magnetismo corre bastante paralela con la de la electricidad; la diferencia más esencial es que las verdaderas cantidades magnéticas residen en las moléculas, y las mensurables adiciones que condicionan la aparición de los polos en imanes finitos se originan por suma de las acciones de moléculas en dirección paralela.

2. Galvanismo y electrólisis.

La historia del descubrimiento de la llamada electricidad de contacto, hecha por Galvani (1780) y Volta (1792), es tan conocida que podemos omitirla aquí; pues, por interesantes que sean los experimentos de Galvani sobre las ranas y la discusión suscitada por ellos sobre el origen de las cargas eléctricas, mas nos interesa la comprensión clara de los conceptos y las leyes. Por eso estableceremos los hechos ante todo.

fig78

Si se sumergen dos metales diferentes en una solución (figura 78), por ejemplo, cobre y cinc en ácido sulfúrico rarificado, presentarán los metales cargas eléctricas, que ejercen exactamente la misma acción que la electricidad de frotamiento. Según la ley fundamental de la electricidad, preséntanse las cargas de ambos signos en los metales (polos) en igual cantidad; el sistema formado por la solución y los metales, llamado también elemento galvánico o célula, posee, pues, la propiedad de separar las electricidades. Lo notable es que tal propiedad es, al parecer, inagotable; pues si se unen los polos por un hilo metálico, de suerte que sus cargas fluyen y se compensan, quedarán cargados los polos tan pronto como se aparte el hilo. El elemento proporciona, pues, constantemente electricidad, mientras existe la unión del hilo metálico; en el hilo debe, pues, verificarse un constante correr de la electricidad. ¿Cómo representárselo? Ello dependerá de la teoría que se adopte, la de uno o de dos flúidos; en el primer caso sólo existe una corriente; en el segundo hay dos corrientes opuestas de los dos flúidos.

La corriente eléctrica demuestra su existencia por efectos muy claros. Sobre todo, calienta el hilo de unión. Todos conocen el hecho, por los hilos de metal en nuestras bombillas de alumbrado eléctrico. La corriente produce, pues, continuamente energía térmica. ¿De dónde tiene el elemento galvánico la propiedad de producir continuamente electricidad y desarrollar así por modo indirecto calor? Según la ley de la conservación de la energía, debe ocurrir que donde se manifieste una clase de energía por cierto proceso, ha de desaparecer otra clase de energía en cantidad igual a la primera.

La fuente de energía es el proceso químico en la célula. Uno de los metales se disuelve mientras dura la corriente; en el otro precipítase un elemento de la solución; en la solución misma pueden verificarse complicados procesos químicos. Nada nos interesan éstos; nos basta el hecho de que las células galvánicas son un medio de producir electricidad en casi ilimitadas cantidades y poner en marcha considerables corrientes eléctricas.

Pero habremos de considerar ahora el proceso inverso, en el cual la corriente eléctrica produce una separación química. Si entre dos hilos de metal indescomponible, de platino, por ejemplo (llámanse electrodos), se hace pasar por agua acidulada la corriente eléctrica, el agua se descompone en los elementos hidrógeno y oxígeno; el hidrógeno se desarrolla en el electrodo negativo (cátodo) y el oxigeno en el positivo (ánodo). Las leyes cuantitativas de esa electrólisis, descubierta por Nicholson y Carlisle (1800), fueron encontradas por Faraday (1832). Sabido es cuán enorme trascendencia han tenido las investigaciones de Faraday para el conocimiento de la estructura de la materia y para la química teórica y técnica; pero no es esto lo que nos invita a detenernos algo en este punto, sino la circunstancia de que las leyes de Faraday dan los medios para medir exactamente las corrientes eléctricas, y de esa suerte hácese posible la construcción del sistema de los conceptos electromagnéticos.

El experimento de descomposición puede hacerse, igualmente que con una corriente galvánica, con una corriente de descarga, la cual se produce cuando se unen por un hilo metálico dos cuerpos de metal cargados con cargas contrarias. Desde luego, hay que cuidar, en este caso, de que las cantidades de electricidad que vienen a descargarse sean bastante grandes; tenemos aparatos para conservar la electricidad, los llamados condensadores, cuya actuación descansa en el principio de la influencia y que dan tan fuertes descargas, que son descompuestas en la célula electrolítica cantidades mensurables. Los ya explicados métodos de la electroestática no permiten medir la cantidad de carga que corre por la célula. Faraday ha encontrado la ley de que doble carga produce doble descomposición; triple carga, triple descomposición; en suma, que la cantidad m de la materia descompuesta (o de uno de los dos productos de descomposición) es proporcional a la cantidad de electricidad e que ha pasado por él:

$Cm=e$.

La constante C depende de la especie de materia y del proceso químico.

Una segunda ley de Faraday regula esta dependencia. Es sabido que los elementos químicos entran en combinación según proporciones de peso muy determinadas. Desígnase como peso equivalente la cantidad de un elemento que se combina con 1 g. del elemento más ligero, el hidrógeno. Así, por ejemplo, en el agua (H₂O) combínanse 8 g. de oxígeno (O) con 1 g. de hidrógeno (H) por lo cual el oxígeno tiene el peso equivalente 8. La ley de Faraday dice, pues, que la misma cantidad de electricidad que separa 1 g. de hidrógeno puede separar de cualquier otro elemento un peso equivalente, esto es, por ejemplo, 8 g. de oxígeno.

La constante C no necesita, pues, ser conocida sino para el hidrógeno; obtiénese luego para cualquier otro cuerpo, dividiendo por el peso equivalente. Para 1 g. de hidrógeno tenemos:

$C_{0}\cdot 1=e$.

Para otro cuerpo cuyo peso equivalente sea μ, tendremos:

$C_{\mu }=e$;

y dividiendo las dos ecuaciones se sigue:

${\frac {C}{C_{0}}}={\frac {1}{\mu }},\quad C={\frac {C_{0}}{\mu }}.$

Es, pues, C₀=e la cantidad de electricidad que separa 1 g. de hidrógeno; su valor numérico se establece por mediciones exactas, y es, en el sistema c, g, s.:

$C_{0}=2,90\cdot 10^{11}$ unidades de carga por gramo.[44]

Y ahora pueden unirse las dos leyes de Faraday en esta fórmula:

$e={\frac {C_{0}}{\mu }}m$.[45]

La descomposición electrolítica ofrece, pues, una medida comodísima para la cantidad de electricidad e que ha pasado en la célula en una descarga; basta determinar la masa m de un producto de descomposición cuyo peso equivalente sea μ, y se obtiene por la ecuación [45] la cantidad de electricidad que se busca. Y es, naturalmente, indiferente que se haya obtenido ésta por descarga de conductores cargados (condensadores) o que proceda de una célula galvánica. En este último caso, la electricidad corre continuamente con fuerza constante; la cantidad que pasa en la unidad de tiempo por una sección cualquiera de la conducción y, por tanto, por la célula de descomposición, llámase fuerza de la corriente. Esta puede medirse simplemente haciendo pasar la corriente galvánica durante la unidad de tiempo (1 sec.) por la célula electrolítica y determinando la masa m de un producto de descomposición; entonces la ecuación [45] proporciona la carga e, que es igual a la fuerza de la corriente. Si la corriente pasa, no durante un segundo, sino durante t segundos, entonces la cantidad de electricidad e que ha corrido y la masa m separada de cada producto de descomposición son t veces el número anterior; la fuerza de la corriente J es, pues:

$J={\frac {e}{t}}={\frac {C_{0}}{\mu }}\cdot {\frac {m}{t}}$.[46]

Su dimensión es:

$[J]=\left[{\frac {e}{t}}\right]=\left[{\frac {l}{t}}{\sqrt {K}}\right]=\left[{\frac {l}{t^{2}}}{\sqrt {ml}}\right]$,

y su unidad:

${\frac {{\text{cm.}}{\sqrt {\text{g.cm.}}}}{{\text{sec.}}^{2}}}$.

3. Resistencia y calor de la corriente.

fig79

Ahora debemos ocuparnos un poco del proceso mismo de la corriente. Se ha comparado siempre la corriente eléctrica con la corriente de agua en una conducción tubular y se han aplicado al proceso eléctrico las leyes que rigen en el otro. Para que el agua corra por un tubo, tiene que existir una fuerza de impulsión; si el agua sale de un vaso más alto por un tubo inclinado, para entrar en un vaso más bajo, será la gravedad la fuerza impulsiva (figura 79). Y ésta es tanto mayor cuanto más alta está la superficie superior del agua sobre la inferior. Pero la velocidad de la corriente de agua o su fuerza de corriente no depende sólo de la cantidad del impulso por la gravedad, sino, además, de la resistencia que el agua encuentra en el tubo conductor. Si éste es largo y estrecho, la cantidad de agua impulsada por unidad de tiempo es más pequeña que si el tubo es corto y ancho. La fuerza de la corriente, J, es, pues, proporcional a la resistencia W; establecemos

$J={\frac {V}{W}}$ ó $JW=V$;[47]

en donde se elige por unidad de resistencia la que produce una fuerza de corriente = 1 con una diferencia de nivel v = 1.

Estas mismas representaciones las ha aplicado G. S. Ohm (1826) a la corriente eléctrica. A la diferencia de nivel, que es el impulso, corresponde la fuerza eléctrica; para un determinado trozo de hilo metálico de longitud l, es V = El, siendo E la fuerza del campo que se considera constante a lo largo del hilo. Pues si el mismo campo eléctrico actúa sobre una mayor longitud de hilo, le da mayor impulsión a la electricidad corriente. La cantidad V se llama también tensión o fuerza electromotora; es, además, idéntica al concepto de potencial eléctrico, que ya antes hemos citado (pág. 174).

Como la fuerza de la corriente J y la fuerza del campo eléctrico, por tanto la tensión V = El también, son cantidades mensurables, cabe comprobar experimentalmente la proporcionalidad entre J y V, que expresa la ley de Ohm [47].

La resistencia W depende del material y de la forma del hilo conductor; cuanto más largo y fino sea éste, tanto mayor es W. Si l es la longitud del hilo y q la dimensión de su sección, será W directamente proporcional a l, e indirectamente proporcional a q; escríbese, pues:

$\sigma W={\frac {l}{q}}$ ó $W={\frac {l}{\sigma q}}$;[48]

en donde el factor de proporcionalidad σ depende solamente del material del hilo, y se llama capacidad conductora.

Si se elimina W de la fórmula [48] y se introduce V = El en la [47] se obtiene

$JW=J{\frac {l}{q\sigma }}=V=El$,

y de aquí se sigue, eliminando l:

${\frac {J}{q\sigma }}=E$ ó ${\frac {J}{q}}=\sigma E$

Pero ${\tfrac {J}{q}}$ significa la fuerza de la corriente por unidad de la sección; llámase densidad de la corriente, y se designa con la letra i. Entonces se establece:

$i=\sigma E$.[49]

En esta forma, la ley de Ohm no contiene ya mas que una constante característica del material conductor, la capacidad conductora σ, pero nada más, que dependa de la forma del cuerpo conductor (hilo metálico).

Para los no conductores (aisladores) es σ = 0. Pero no existen aisladores ideales; siempre existen pequeños rastros de capacidad conductora, salvo en el perfecto vacío. Conócense todos los tránsitos desde los malos conductores (porcelana, ámbar), pasando por los conductores medianos o semiconductores (agua y otros electrólitos) hasta los metales, que poseen una enorme capacidad de conducción.

Ya antes hemos observado que la corriente calienta el hilo. La ley cuantitativa de este fenómeno ha sido hallada por Joule (1841); es manifiestamente un caso especial de la ley de la conservación de la energía, transformándose la energía eléctrica en calor. La ley de Joule dice que el calor desarrollado por la corriente J al pasar la tensión V en la unidad de tiempo, es igual a

$Q=JV$;[50]

donde Q debe medirse no en calorías, sino en unidades mecánicas de trabajo. No haremos en lo sucesivo uso de esta fórmula, y sólo la damos por ser completos en la exposición de este punto.

4. Electromagnetismo.

Hasta ahora hemos considerado la electricidad y el magnetismo como dos esferas de fenómenos que, si bien tienen muchas semejanzas, son, empero, distintas e independientes. Se ha buscado, como es natural, con gran afán la unión entre ambas esferas; pero sin éxito, durante mucho tiempo. Por último, Oersted (1820) descubrió que las agujas magnéticas son desviadas por corrientes galvánicas. En el mismo año hallaron Biot y Savart la ley cuantitativa de este fenómeno que Laplace formuló como acción a distancia. Es, por tanto, de gran importancia para nosotros, porque en ella aparece por vez primera una constante característica del electromagnetismo, constante que tiene la naturaleza de una velocidad y que luego se ha manifestado idéntica a la velocidad de la luz.

fig80

Biot y Savart establecieron que la corriente que pasa por un hilo recto ni atrae ni repele un polo magnético, sino que tiende a empujarlo en un círculo alrededor del hilo (fig. 80) y en el sentido de una rotación a la derecha (contraria a las agujas del reloj) en derredor a la dirección (positiva) de la corriente. La ley cuantitativa puede reducirse a la forma más sencilla, pensando el hilo conductor dividido en pequeños trozos de longitud e indicando la acción de esos elementos de corriente, de donde luego se obtiene por suma el efecto de la corriente total. Nos limitaremos a indicar la ley de un elemento de corriente, para el caso especial de que el polo magnético está en el plano que pasa por el centro del elemento y es perpendicular a la dirección del mismo (fig. 81). En este caso, la fuerza de valor 1, actuando sobre el polo magnético, o sea la fuerza del campo magnético H, está en ese plano y es perpendicular a la línea que une el polo con el centro del elemento de corriente y es directamente proporcional a la fuerza de la corriente J y a su longitud l, siendo inversamente proporcional al cuadrado de la distancia r. Tenemos, pues:

fig81

$cH={\frac {Jl}{r^{2}}}$.[51]

Exteriormente, esta fórmula tiene semejanza con la ley de la atracción de Newton, o con la ley de Coulomb de la electroestática y la magnetoestática; pero la fuerza electromagnética es, sin embargo, de muy distinto carácter; pues no actúa en la línea de unión, sino perpendicularmente a ella. Las tres direcciones J, r, H son perpendiculares dos a dos; se conoce aquí que las acciones electrodinámicas están estrechamente unidas a la estructura del espacio euclidiano; dan, en cierto modo, un sistema natural de coordenadas rectangulares.

El factor de proporcionalidad c, introducido en la fórmula [51], está totalmente determinado, pues la distancia r, la fuerza de la corriente J y el campo magnético H, son cantidades mensurables. Significa evidentemente la fuerza de una corriente tal que, pasando por un trozo de conducción de longitud 1, a la distancia 1, produce el campo magnético 1. Es corriente y muchas veces cómodo, en lugar de tomar la unidad de corriente que hemos introducido (a saber, la cantidad de electricidad estática que en la unidad de tiempo pasa por la sección) y que se llama la unidad electroestática, elegir como unidad de corriente esa corriente de fuerza c en la masa electroestática; llámase entonces unidad electromagnética de corriente. Su uso tiene la ventaja de que la ecuación [51] adquiere la forma sencilla $H={\tfrac {Jl}{r^{2}}}$ ó $J={\tfrac {Hr^{2}}{l}}$, por la cual la medición de una fuerza de corriente se reduce a la de dos longitudes y un campo magnético. La mayor parte de los instrumentos prácticos para medir corrientes descansan en la desviación de agujas magnéticas por las corrientes, o inversamente, y dan, por tanto, la fuerza de la corriente en la masa electromagnética. Para calcular la conversión a la masa electrostática de la corriente, que es la que primeramente hemos introducido, tiene que ser conocida la constante c; pero para esto basta con una sola medición.

Antes de hablar de la determinación experimental de la cantidad c, vamos a informarnos de su naturaleza, merced a una sencilla consideración de dimensión. Es ésta definida, según la fórmula [51], por la fórmula $c={\tfrac {Jl}{Hr^{2}}}$.

Ahora bien; rigen las siguientes fórmulas de dimensión:

$J=\left[{\frac {e}{t}}\right]$, y $H=\left[{\frac {p}{r^{2}}}\right]$.

La dimensión de c es, pues:

$[c]=\left[{\frac {el}{pt}}\right]$

Pero sabemos que la carga eléctrica e y la fuerza del polo magnético p tienen la misma dimensión, porque la ley de Coulomb es la misma para fuerzas eléctricas y magnéticas. De aquí se obtiene:

$[c]=\left[{\frac {l}{t}}\right]$

esto es, que la constante c tiene la dimensión de una velocidad.

Su primera medición exacta fué realizada por Weber y Kohlrausch (1856). Estos experimentos pertenecen a los más admirables trabajos de precisión física, no sólo por su dificultad, sino por el alcance de su resultado. Se vió, en efecto, que el valor de c es 3·10¹⁰ cm./sec.; es decir, que coincide exactamente con la velocidad de la luz.

Esta coincidencia no podía ser casual; muchos pensadores, principalmente Weber mismo, y luego matemáticos como Gauss y Riemann, físicos como Neumann, Kirchhoff y Clausius, sospecharon la profunda conexión que el número c = 3·10¹⁰ cm./sec., establecía entre dos grandes territorios del saber humano, y buscaron el puente que del electromagnetismo conduce a la óptica. Riemann se acercó mucho a la solución del problema; pero no fué ésta conseguida hasta Maxwell, cuando el arte maravilloso de experimentar que poseía Faraday hubo puesto de manifiesto nuevos hechos y nuevas concepciones. Vamos a seguir ahora esta evolución.

5. Líneas de fuerza de Faraday.

Faraday no procedía de una escuela; su espíritu no estaba recargado de representaciones y teorías tradicionales. Su aventurera ascensión de aprendiz de encuadernador a físico de fama mundial en la Royal Institution es bien conocida. Tan libre de esquemas convencionales como fué su vida, fué asimismo el mundo de sus pensamientos, que surgían espontánea y exclusivamente de la muchedumbre de sus experimentales conocimientos. Ya antes hemos hablado de sus investigaciones sobre la descomposición electrolítica. Su método, que consistía en realizar todas las variaciones posible en las condiciones del experimento, le llevó en 1837 a colocar entre las dos placas metálicas (electrodos) de la célula electrolítica, en lugar de un liquido conductor (ácido, solución salina) un líquido no conductor, como petróleo o trementina. Estos cuerpos no se descomponen, pero no dejan de tener influjo en el proceso eléctrico. Se ve, en efecto, que las dos placas de metal, cuando se cargan por medio de una determinada batería galvánica con determinada tensión, admiten muy diferentes cargas, según la substancia que se encuentra entre ellas (fig. 82). La substancia no conductora influye, pues, en la capacidad del sistema de conductores que consiste en las dos placas y que se llama condensador.

fig82

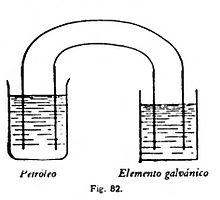
Este descubrimiento produjo en Faraday tal impresión que, a partir de este instante, renunció a las representaciones corrientes de la electroestática de una inmediata acción a distancia de las cargas eléctricas, y desenvolvió una nueva peculiar interpretación de los fenómenos eléctricos y magnéticos que puede caracterizarse como teoría de la acción próxima. Lo que Faraday aprendió en el experimento citado es el hecho de que las cargas de las dos placas de metal no actúan simplemente unas sobre otras por el espacio intermedio, sino que el medio que se encuentra en ese espacio tiene un papel esencial. De aquí infirió que la acción se propaga por ese medio de lugar a lugar, y que es, por tanto, una acción próxima.

fig83

Ya conocemos la acción próxima de las fuerzas elásticas en cuerpos sólidos deformados. Faraday, que siempre se atenía a los hechos empíricos, comparó, sin duda, la acción próxima de la electricidad en no conductores con las vibraciones elásticas; pero se abstuvo de aplicar las leyes de éstas a los fenómenos eléctricos. Usa la imagen de las líneas de fuerza, que cruzan en la dirección de los campos eléctricos desde las cargas positivas, por el aislador, a las negativas; en el caso de un condensador de placas, las líneas de fuerza son líneas rectas perpendiculares a los planos de las placas (fig. 83). Faraday considera las líneas de fuerza como el substrato propio de los procesos eléctricos; son para él verdaderas formaciones materiales que se mueven y deforman y producen así los efectos eléctricos. Las cargas tienen, para Faraday, un papel enteramente subordinado; son los lugares de donde salen o en donde terminan las líneas de fuerza. Esto concepción halló confirmación en experimentos que demuestran que, en los conductores, la carga eléctrica reside toda ella en la superficie, dejando el interior perfectamente libre. Para demostrarlo, construyó un gran cajón, cubierto de metal todo en derredor, y se metió en él con instrumentos de medición eléctrica muy sensibles; luego hizo cargar el cajón con gran fuerza y determinó que en el interior no se advertía la más mínima influencia de las cargas. De aquí concluyó que la carga no es lo primario en los procesos eléctricos y que no debe representarse como flúido provisto de fuerzas que actúan a distancia, sino que lo primario es el estado de tensión del campo eléctrico en los no-conductores, que queda expuesto en la imagen de las líneas de fuerza; los conductores son, en cierta manera, agujeros en el campo eléctrico, y las cargas en ellos son sólo conceptos ficticios inventados para interpretar como acciones a distancia las fuerzas de presión y tracción producidas por las tensiones del campo. Entre las substancias no conductoras o «dieléctricas» hállase también el vacío, el éter, que se nos presenta nuevamente ahora con distinto ropaje.

Esta extraña concepción de Faraday no obtuvo al principio, entre los físicos y los matemáticos de su tiempo, ninguna aceptación. Mantuviéronse firmes en conservar la concepción de la acción a distancia, y ésta pudo desenvolverse aun teniendo en cuenta la acción dieléctrica de los no-conductores, descubierta por Faraday. Bastaba, en efecto, alterar un poco la ley de Coulomb; a todo no-conductor le corresponde una constante característica ε, su constante de dielectricidad, que se define por este hecho: que la fuerza actuante entre dos cargas e₁ y e₂, que descansan en el no-conductor, es más pequeña que en el vacío en la proporción 1:1:

$K={\frac {1}{\varepsilon }}{\frac {e_{1}e_{2}}{r^{2}}}$.[52]

Para el vacío es ε = 1; para cualquier otro cuerpo es ε < 1.

Con este añadido podían, efectivamente, explicarse todos los fenómenos de la electrostática, teniendo en cuenta las propiedades dieléctricas de los no-conductores. Ya hemos dicho antes que la electrostática había pasado formalmente hacia ya tiempo a ser una teoría de pseudoacción próxima, la llamada teoría del potencial. Esta pudo fácilmente también asimilar la constante de dielectricidad ε. Hoy sabemos que de esa manera quedaba ya propiamente adquirida la fomulación matemática del concepto de «línea de fuerza» establecido por Faraday. Pero, como este método del potencial pasaba por un simple artificio matemático, quedaba sin resolver la oposición entre la teoría clásica de la acción a distancia y la representación de Faraday basada en acción próxima.

Muy análogas concepciones desenvolvió Faraday para el magnetismo. Descubrió que también las fuerzas entre dos polos magnéticos dependen del medio que entre ellos se encuentre, y llegó así a la concepción de que las fuerzas magnéticas, como las eléctricas, son producidas por un peculiar estado de tensión de los medios intermedios. Para exponer esas tensiones sirviéronle las líneas de fuerza; pueden verse incluso estas lineas, esparciendo sobre un papel limadura de hierro y manteniendo éste pegado a un imán (fig. 84).

fig84

La teoría de la acción a distancia introduce formalmente una constante característica de la substancia, la permeabilidad magnética μ, y escribe la ley de Coulomb en la siguiente forma alterada:

$K={\frac {1}{\mu }}{\frac {p_{1}p_{2}}{r^{2}}}$.[53]

Pero no ha bastado esta alteración formal, sino que se ha inventado un mecanismo molecular que hace inteligible la polarizabilidad magnética y dieléctrica. Ya hemos visto antes que las propiedades de los imanes conducen a considerar sus moléculas mismas como pequeños imanes elementales, que en el proceso de la magnetización se dirigen paralelamente. Admítese en esto que conservan por sí la disposición paralela, acaso a consecuencia de resistencias de frotamiento. Puede admitirse que en la mayor parte de los cuerpos que no se presentan como imanes permanentes falta ese frotamiento; entonces la posición paralela será producida por un campo magnético exterior; pero desaparecerá al punto, tan pronto como se aleje el campo. Una substancia tal será, pues, imán sólo durante el tiempo en que se halle junto a ella un campo magnético exterior. Pero no hace falta ni siquiera admitir que las moléculas sean imanes permanentes, en posición paralela; si cada molécula contiene los dos flúidos magnéticos, éstos se separarán bajo la acción del campo y la molécula por sí misma será un imán. Este magnetismo inducido ha de tener, empero, la misma acción que la teoría formal describe introduciendo la permeabilidad. Entre dos polos magnéticos (N y S) en tal medio, fórmanse cadenas de moléculas-imanes cuyos polos opuestos compénsanse en el interior; pero terminan en N y S en polos opuestos, y así debilitan las acciones de N y S (fig. 85). Prodúcese, por lo demás, también el efecto inverso de la fortificación; pero no entraremos aquí en su interpretación.

fig85

fig86

Exactamente lo mismo que acabamos de explicar para el magnetismo puede pensarse también para la electricidad. Un dieléctrico consiste, según esto, en moléculas que, o son por sí mismas dipolos eléctricos y se dirigen paralelamente, en un campo exterior, o que por la acción del campo llegan a ser dipolos merced a la separación de la electricidad positiva y la negativa. Entre dos placas de un condensador fórmanse entonces cadenas de moléculas (fig. 86), cuyas cargas se compensan en el interior, pero no junto a las placas. Por lo tanto, una parte de la carga de las placas mismas es anulada y hay que añadir a las placas nueva carga para cargarla a determinada tensión. Así se explica que el dieléctrico polarizable aumente la capacidad del condensador.

Según esta representación de la teoría de la acción a distancia, es la acción del dieléctrico una acción mediata. El campo en el vacío es sólo una abstracción; significa la distribución geométrica de la fuerza que sería ejercida sobre un cuerpo de prueba por la carga 1. El campo en el dieléctrico consiste, empero, en una alteración física verdadera, el desplazamiento molecular de las electricidades.

La teoría de la acción próxima de Faraday no reconoce tal diferencia entre el campo en el éter y en la materia aisladora: ambos son dieléctricos; para el éter la constante de dielectricidad es ε = 1; para otros aisladores es diferente de 1. Si la imagen intuitiva del desplazamiento eléctrico es exacta para la materia, habrá de valer también para el éter. Este pensamiento juega un papel importantísimo en la teoría de Maxwell, que, en el fondo, no es mas que la traducción de la representación de las «lineas de fuerza» de Faraday al lenguaje exacto de la matemática. Admite que también en el éter la producción de un campo eléctrico o magnético va acompañada de «desplazamientos» de los flúidos. No hace falta para ello representarse el éter como constituido por átomos; pero el pensamiento de Maxwell aparece con la máxima claridad, si nos figuramos moléculas de éter, las cuales, como las moléculas materiales, tórnanse dípolas en el campo. El campo, empero, no es la causa de esta polarización, sino que el desplazamiento es la esencia del estado de tensión, que se llama campo eléctrico; las cadenas de moléculas de éter son las líneas de fuerza y las cargas en las superficies de los conductores no son sino las cargas terminales de esas cadenas. Si, además de las partículas de éter, hay también moléculas materiales, la polarización se fortifica y las cargas en las extremidades se hacen mayores.

Ahora bien; ¿cuáles son exactas, las representaciones de Faraday y Maxwell, o las de la teoría de la acción a distancia?

Mientras nos movemos en el circulo de los fenómenos electro y magnetostáticos, son ambas teorías aquivalentes por completo. Pues la expresión matemática del pensamiento de Faraday es lo que hemos llamado una pseudoacción próxima, porque, si bien opera con ecuaciones diferenciales, no conoce, sin embargo, una velocidad finita de propagación de las tensiones. Mas Faraday y Maxwell mismos son los que han descubierto los procesos que, análogos a los efectos de inercia en la mecánica, dan por resultado el retraso de la propagación de un estado electromagnético de lugar en lugar y, por tanto, la velocidad finita de propagación. Son la inducción magnética y la corriente de desplazamiento.

6. La inducción magnética.

Después que Oersted hubo descubierto la producción de un campo magnético por una corriente eléctrica; cuando Biot y Savart la formularon como acción a distancia, halló Ampere (1820) que dos corrientes galvánicas ejercen recíprocamente acciones de fuerza, y consiguió asimismo expresar la ley de este fenómeno en el lenguaje de la teoría de la acción a distancia. Este descubrimiento tuvo amplias consecuencias, pues permitió reducir el magnetismo a la electricidad. Según Ampere, en las moléculas de los cuerpos magnetizables deben pasar pequeñas corrientes cerradas; demostró que éstas se comportan exactamente como imanes elementales. Esta idea se ha comprobado enteramente; a partir de ahora, los flúidos magnéticos ya son superfluos; no hay mas que electricidad, que si permanece inmóvil, produce el campo electrostático y, si se hace corriente, produce además el campo magnético. El descubrimiento de Ampere puede expresarse también como sigue: un hilo metálico recorrido por la corriente J₁ produce, según Oersted, un campo magnético en su proximidad; un segundo hilo, en el que corre la corriente J₂, experimenta entonces acciones de fuerza en este campo magnético. El campo magnético actúa, pues, manifiestamente sobre la electricidad de corriente, desviándola o acelerándola.

Pero entonces se plantea la cuestión siguiente: ¿no podrá el campo magnético poner en movimiento electricidad que esté en reposo? ¿No podrá producir o «inducir» una corriente en el segundo hilo primitivamente privado de corriente?

A esta pregunta ha contestado Faraday (1831). Halló que un campo magnético estático no tiene la propiedad de producir una corriente; pero que surge una corriente tan pronto como se altera el campo magnético. Si, por ejemplo, acercaba de repente un imán a un hilo de conducción cerrado, fluía en el hilo una corriente, mientras duraba el movimiento; o bien, si producía el campo magnético por medio de una corriente primaria, surgía en el segundo hilo, secundario, un corto impulso de corriente, siempre que insertaba o separaba la corriente primera.

fig87

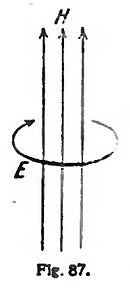
De aquí se sigue que la fuerza eléctrica inducida depende de la temporal variación de velocidad del campo magnético. Consiguió Faraday, merced a sus líneas de fuerza, formular la ley cuantitativa del fenómeno. Queremos dar a esta ley una forma tal que se manifieste claramente su analogía con la ley de Biot y Savart. Representémonos un haz de líneas de fuerza magnéticas paralelas, que constituyen un campo magnético, H; alrededor de éste, figurémonos un hilo conductor en forma circular (fig. 87). Si el campo H varía en el breve tiempo t en la cantidad h, llamaremos ${\tfrac {h}{t}}$ la velocidad de su variación o la variación del número de líneas de fuerza. Representémonos las líneas de fuerza como cadenas de dípolos magnéticos (lo cual propiamente no está permitido, según Ampere) entonces, al variar H se producirá en cada molécula de éter un desplazamiento de las cantidades magnéticas, o sea «una corriente magnética de desplazamiento», cuya fuerza por unidad de superficie, o sea densidad de corriente, está dada por $j={\tfrac {h}{t}}$ . Si el campo H no está en el éter, sino en una substancia de permeabilidad μ, será la densidad de la corriente magnética de desplazamiento $j=\mu {\tfrac {h}{t}}$. Por la sección q, o sea la superficie del círculo formado por el hilo conductor, pasa, pues, la corriente magnética

$J=qj=q\mu {\frac {h}{t}}$.

Esto produce ahora, según Faraday, todo en derredor un campo eléctrico E, que envuelve exactamente la corriente magnética, como en el experimento de Oersted el campo magnético H la corriente eléctrica; pero en dirección opuesta. Ese campo eléctrico E es el que impulsa la corriente inducida en el hilo conductor; existe, aun cuando no haya ningún hilo conductor en el cual pueda formarse una corriente.

fig88

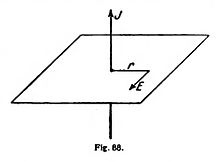
Se ve que la inducción magnética de Faraday es enteramente paralela al descubrimiento electromagnético de Oersted. La ley cuantitativa es también la misma exactamente. Allá, según Biot y Savart, el campo magnético H producido por un elemento de corriente de longitud l y de fuerza J (véase figura 81, pág. 184), era, en el plano perpendicular al elemento, perpendicular a la línea de unión r y a la dirección de la corriente y tenia el valor $H={\tfrac {Jl}{cr^{2}}}$ (fórmula [51], pág. 184).

Aquí ocurre exactamente lo mismo si se truecan las magnitudes eléctricas y magnéticas y al mismo tiempo el sentido de la rotación (fig. 88); el campo eléctrico inducido está dado por

$E={\frac {Jl}{cr^{2}}}$

Aparece la misma constante c, la relación de la unidad de corriente electromagnética con la electrostática, cuyo valor ha sido encontrado por Weber y Kohlrausch igual a la velocidad de la luz. Que ello debe ser así, puede conocerse, además, mediante consideraciones de orden energético.

Sobre la ley de inducción descansa una gran parte de las aplicaciones físicas y técnicas de la electricidad y el magnetismo. El transformador, el inductor, la dínamo y muchos otros aparatos y máquinas son dispositivos para inducir corrientes eléctricas por medio de campos magnéticos alternantes. Pero aunque estas cosas son muy interesantes, no se hallan, sin embargo, en nuestro camino, que se endereza a la investigación del éter en relación con el problema del espacio. Pasaremos, pues, inmediatamente a exponer la teoría de Maxwell, cuyo gran objeto fué comprender todos los fenómenos electromagnéticos conocidos en una teoría coherente de acción próxima, en el sentido de Faraday.

7. La teoría de la acción próxima de Maxwell.

Ya hemos dicho antes que la electrostática y la magnetostática fué reducida por los matemáticos, poco después del establecimiento de la ley de Coulomb, a la forma de una teoría de pseudoacción próxima. El problema de Maxwell fué fundir ésta con las representaciones de Faraday y darle así una forma tal, que comprendiera también los fenómenos recién descubiertos de la polarización dieléctrica y magnética, del electromagnetismo y de la inducción magnética.

Maxwell pone a la base de su doctrina la ya referida representación de que un campo eléctrico E va acompañado siempre de un desplazamiento eléctrico εE, no sólo en la materia, donde ε > 1, sino también en el éter, donde ε = 1. Ya hemos expuesto antes cómo es posible representarse intuitivamente este desplazamiento merced a la separación y corriente de los flúidos eléctricos en las moléculas.

Lo primero que Maxwell establece es el hecho de que, fundándose en la representación del desplazamiento, la ley de Coulomb no es, en el fondo, mas que una consecuencia de la ley de la indestructibilidad de la electricidad.

fig89

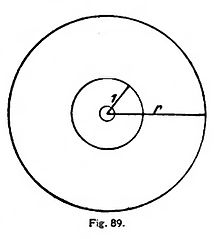
Imaginemos una esfera metálica en un medio que posea la constante de dielectricidad ε (figura 89). En éste construímos una esfera de radio 1 y otra esfera de radio r. Ahora es cargada la esfera metálica con la cantidad de electricidad positiva e. Según Maxwell, deberá producirse en cada molécula del dieléctrico un desplazamiento de la electricidad positiva hacia afuera, para que la cantidad de electricidad contenida en un volumen cualquiera permanezca constante. Ahora bien; la cantidad de electricidad desplazada por la superficie de una esfera de radio 1 se mide, según Maxwell, por εE. Por cada esfera concéntrica pasará la misma cantidad de electricidad, porque, de lo contrario, formaríase en el dieléctrico un amontonamiento de cargas. Mas las superficies de dos esferas son como los cuadrados de los radios, de donde resulta que por la esfera de radio r pasa la cantidad de electricidad r²εE.

Mas ésta debe ser exactamente igual a la carga e de la esfera metálica, en donde halla su término el desplazamiento; por lo tanto, r²εE=e, o sea:

$E={\frac {e}{\varepsilon r^{2}}}$

Pero ésta es justamente la ley de Coulomb en la forma generalizada [53] de la página 190; E es la fuerza ejercida por la carga e sobre la unidad de carga a la distancia r.

Si no se trata de esferas, sino de cuerpos cargados cualesquiera, permanece idéntica la idea fundamental de Maxwell: el campo hállase determinado por la condición de que el desplazamiento εE de la electricidad en el dieléctrico hacia fuera, o la «divergencia» de εE (div. εE) por una superficie cualquiera, tan pequeña como se quiera, compensa las cargas que se producen en el interior de la superficie. Designando con ρ la carga por unidad de volumen o densidad de carga de la electricidad, escribiremos simbólicamente:

${\text{div.}}\varepsilon E=\rho$.[54]

Esto debe servirnos solamente de ayuda para recordar la ley que acabamos de formular. Pero Mawxell demostró que puede derivarse una determinada expresión diferencial para el concepto de divergencia; por lo cual la fórmula [54] significa para el matemático una ecuación diferencial, una ley de acción próxima.

Las mismas reflexiones exactamente valen para el magnetismo, con una importante diferencia: según Ampere, no hay propiamente imanes, no hay cantidades magnéticas, sino sólo electroimanes. El campo magnético debe ser producido siempre por corrientes eléctricas, ya sea por corrientes conducidas en hilos, ya sea por corrientes moleculares en las moléculas. De aquí se sigue que las líneas de fuerza magnéticas no terminan, no rematan nunca, sino que, o retroceden sobre sí mismas, o se pierden en lo infinito. Tal es el caso en un electroimán, en una bobina atravesada por una corriente (fig. 90); las líneas de fuerza magnética van en línea recta por el interior de la bobina, y algunas se cierran por fuera, mientras otras se van al infinito. Si imaginamos la bobina cerrada por dos planos A, B, entrará por A tanto «desplazamiento magnético» μH como el que sale por B; por lo demás, como en esto no cuadra bien la imagen de un desplazamiento, se dice generalmente «inducción magnética», en lugar de desplazamiento. Por una superficie cerrada cualquiera entrarán siempre tantas líneas de fuerza como salen de ella; es decir, que la «divergencia» total del magnetismo por una superficie cerrada cualquiera es igual a cero.

${\text{div.}}\mu H=0$.[55]

Esta es la fórmula de acción próxima que Maxwell da del magnetismo.

fig90 y fig91

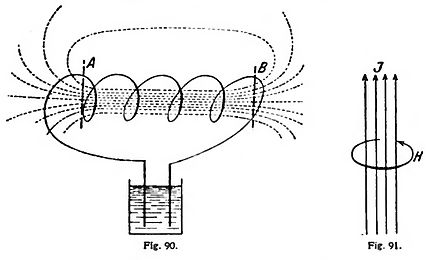
Llegamos ahora a la ley del electromagnetismo, dada por Biot y Savart. Para transformarla en ley de acción próxima, imaginemos la corriente eléctrica distribuida, no en un hilo fino, sino regularmente con la densidad $i={\tfrac {J}{q}}$ sobre una sección circular q, y preguntemos por el campo magnético H, al borde de la sección (fig. 91). Este se halla, según Biot y Savart, en la dirección de la tangente al círculo, y tiene, según la fórmula [51] (pág. 184), el valor $H={\tfrac {Jl}{cr^{2}}}$, donde r es el radio del circulo y l la longitud del elemento de corriente. Mas la sección, la superficie del círculo es igual a πr²; por tanto, la fórmula [51] puede escribirse:

${\frac {cH}{\pi l}}={\frac {J}{\pi r^{2}}}={\frac {J}{q}}=i$,

y esto vale para toda sección, por pequeña que sea, y para toda longitud l, por pequeña que sea. A la izquierda está, pues, cierta cantidad diferencial del campo magnético y la ley dice que es proporcional a la densidad de corriente. La investigación matemática exacta de esta formación diferencial no podemos establecerla aquí; debe tener en cuenta, no sólo la cantidad, sino también la dirección del campo magnético, y como éste gira alrededor de la dirección de la corriente, llámase «rotación» del campo H (rot. H) la operación diferencial. Podemos, pues, escribir simbólicamente:

$c\ {\text{rot.}}H=i$,[56]

y concebimos esta fórmula también como ayuda mnemotécnica para la conexión de la dirección y cantidad del campo magnético H con la densidad de la corriente i. Pero para el matemático es una ecuación diferencial de especie semejante a la ley [54].

Otro tanto puede decirse de la inducción magnética; pero escribiremos el signo opuesto, para indicar que el sentido de la rotación es contrario:

$c\ {\text{rot.}}E=-i$,[57]

Las cuatro fórmulas simbólicas [54], [55], [56] y [57] tienen una admirable simetría. Tal belleza formal no es indiferente en manera alguna; descúbrenos la sencillez del acontecer natural, que permanece oculta a la intuición directa por la limitación de nuestros sentidos, y sólo se manifiesta al intelecto que analiza.

8. La corriente de desplazamiento.

Pero esa simetría no es aún perfecta, pues i significa la densidad de la corriente eléctrica, esto es, un transporte de cargas eléctricas sobre distancias finitas, y j es la variación temporal del campo magnético, y sólo fundándose en la muy artificiosa hipótesis de los dípolos de éter puede interpretarse como corriente de desplazamiento.

Maxwell observó (1864) que lo que para el campo magnético es justo, es para el campo eléctrico aplicable. La representación de los dípolos obliga a admitir también una corriente dieléctrica de desplazamiento, que pasa por los no-conductores, cuando se altera el campo eléctrico E; si llamamos e a la alteración o variación de E en el tiempo t, resulta que la densidad de la corriente dieléctrica de desplazamiento es igual a $\epsilon ={\tfrac {e}{t}}$.

fig92

Esta teoría de Maxwell, que en nuestra exposición casi parece trivial, es de enorme importancia, pues luego fué la clave de la teoría electromagnética de la luz. Vamos a explicar claramente su sentido en un caso concreto. Los polos de una célula galvánica los unimos por dos hilos a las placas de un condensador; en uno de los dos hilos ponemos una llave o interruptor (figura 92). Si se cierra éste, pasa una corta corriente, que carga las dos placas del condensador; entre éstas se produce un campo eléctrico E. Antes de Maxwell se consideraba este proceso como «corriente abierta»; pero Maxwell dice que, mientras aumenta el campo E entre las placas del condensador, corre una corriente de desplazamiento que completa la corriente conducida y la cierra. Tan pronto como las placas del condensador están cargadas, cesan ambas corrientes, la conducida y la de desplazamiento.

Lo esencial es que Maxwell sostiene que la corriente de desplazamiento produce, lo mismo que la corriente conducida, un campo magnético según la ley de Biot y Savart. Y, en efecto, es así; lo han demostrado no sólo los éxitos de la teoría de Maxwell, por su exacta predicción de numerosos fenómenos, sino la experimentación misma que más tarde ha conseguido manifestarlo directamente.

En un semiconductor se presentarán a la vez la corriente conducida y la de desplazamiento. Para la primera rige la ley de Ohm [49] (pág. 182): i=σE; para la segunda rige la ley de Maxwell: $i={\tfrac {\epsilon e}{t}}$; si las don son simultáneas, será

$i=\epsilon {\frac {e}{t}}+\sigma E$.

Para el magnetismo no hay, empero, corriente conducida y siempre es $i=\mu {\tfrac {h}{t}}$. Inclúyase esto en las cuatro ecuaciones simbólicas [54], [55], [56], [57], y serán éstas:

${\begin{cases}{\text{a)}}\ {\text{div.}}\varepsilon E=\rho .\quad &{\text{c)}}\ c\ {\text{rot.}}H-\varepsilon {\frac {e}{t}}=\sigma E\\\\{\text{b)}}\ {\text{div.}}\mu H=0.\quad &{\text{d)}}\ c\ {\text{rot.}}E+\mu {\frac {h}{t}}=0.\end{cases}}$[58]

Y éstas son las leyes de Maxwell, que han sido hasta nuestros días el fundamento de todas las teorías electromagnéticas y ópticas. Para el matemático son muy determinadas ecuaciones diferenciales. Para nosotros son breves reglas mnemotécnicas, que dicen:

a) Dondequiera que se presenta una carga eléctrica, prodúcese un campo eléctrico de tal especie, que en cada volumen la carga es compensada exactamente por el desplazamiento.

b) Por toda superficie cerrada entra tanto desplazamiento magnético como sale.

c) Alrededor de una corriente eléctrica, ya sea conducida, ya de desplazamiento, enróscase un campo magnético.

d) Alrededor de una corriente magnética de desplazamiento enróscase en sentido opuesto un campo eléctrico.

Las «ecuaciones de los campos» de Maxwell, que así son llamadas, constituyen una verdadera teoría de acción próxima; pues, como veremos en seguida, nos dan una velocidad finita para la propagación de las fuerzas electromagnéticas.

Pero en la época en que fueron establecidas estaba aún tan arraigada la fe en la inmediata acción a distancia, según el esquema de la atracción newtoniana, que pasó considerable tiempo hasta que pudieran prevalecer. Pues también la teoría de la acción a distancia había conseguido domeñar con fórmulas los fenómenos de inducción. Para ello hubo que admitir que las cargas en movimiento producen, además de la atracción de Coulomb, otras particulares acciones a distancia, que dependen de la cantidad y dirección de la velocidad. Los primeros ensayos de esta clase proceden de Neumann (1845). Particularmente famosa es la ley que estableció Wilhelm Weber (1846); semejantes fórmulas han dado también Riemann (1858) y Clausius (1877). Todas estas teorías coinciden en explicar las acciones eléctricas y magnéticas por fuerzas entre cargas eléctricas elementales o, como se dice hoy, «electrones»; trátase, pues, de predecesores de la actual teoría de los electrones, faltando desde luego aún una circunstancia esencial: la velocidad finita de propagación de las fuerzas. Estas teorías de la acción a distancia en la electrodinámica dieron una explicación completa de las fuerzas motoras y las corrientes de inducción que se presentan en corrientes conducidas cerradas. Pero en el caso de las corrientes «abiertas», esto es, de las cargas y descargas de los condensadores, hubieron de fracasar, pues en éstas aparece la corriente de desplazamiento de la cual nada saben las teorías de acción a distancia. Helmholtz se ha distinguido particularmente disponiendo apropiados experimentos para decidir entre la teoría de la acción a distancia y la teoría de la acción próxima. Lo consiguió hasta cierto punto y fué él mismo uno de los más celosos defensores de la teoría de Maxwell. Pero su discípulo Hertz fué el que le dió la victoria definitiva, descubriendo las ondas electromagnéticas.

9. La teoría electromagnética de la luz.

Ya hemos hablado antes de la impresión que en los investigadores de aquella época produjo la coincidencia, descubierta por Weber y Kohlrausch, entre la constante electromagnética c y la velocidad de la luz. Pero había aún otros indicios que hacían sospechar que entre la luz y los procesos electromagnéticos debía existir una relación estrecha. Sobre todo lo demuestra el descubrimiento de Faraday (1834) de que un rayo de luz polarizado, que atraviesa un cuerpo magnetizado, es influído por éste; si el rayo va paralelo a las lineas de fuerza magnéticas, su plano de polarización gira. De aquí concluyó Faraday mismo que el éter luminoso y el sustentáculo de las líneas de fuerza electromagnéticas tenían que ser idénticos. Aun cuando no era lo bastante matemático para convertir sus representaciones en leyes y fórmulas cuantitativas, sin embargo, el mundo de sus pensamientos era de índole sumamente abstracta y no estaba atenido, ni mucho menos, a los estrechos límites de la intuición trivial que confunde lo habitual con lo conocido. El éter de Faraday no era un medio elástico; no recibía sus propiedades de analogías con el mundo material, al parecer conocido, sino de experimentos exactos y de las conexiones, verdaderamente conocidas, que de ellos se derivan. Maxwell ha continuado la obra de Faraday; sus dotes eran semejantes a los de Faraday, pero con la posesión y dominio perfecto de los auxilios matemáticos de su tiempo.

Ahora vamos a comprender claramente cómo de las «leyes de los campos» de Maxwell se deriva la propagación de las fuerzas electromagnéticas con velocidad finita. Nos limitamos a procesos en el vacío o éter; éste no posee capacidad conductora, σ = 0, no tiene verdaderas cargas, ρ = 0, y su constante de dielectricidad y su permeabilidad son iguales ε = 1, μ= 1. En tales condiciones, las dos primeras ecuaciones de los campos [58] serán:

${\text{div.}}E=0,\quad {\text{div.}}H=0$.[59]

y expresan que todas las líneas de fuerza son cerradas o van al infinito. Para obtener una imagen, aunque sea grosera, del proceso vamos a representarnos líneas de fuerza singulares, cerradas.

Las otras dos ecuaciones de los campos dicen:

${\frac {e}{t}}=c\ {\text{rot.}}H$,$\quad {\frac {h}{t}}=-c\ {\text{rot.}}E.$[60]

Admitamos, empero, que en cierto espacio limitado domina un campo eléctrico E que varía en el pequeñísimo tiempo t de una cantidad e; su velocidad de variación será ${\tfrac {e}{t}}$. Según la ecuación primera enróscase en ese campo, al momento, un campo magnético que es proporcional a la velocidad de variación ${\tfrac {e}{t}}$; este campo también variará, durante un pequeño tiempo consecutivo t, de una cantidad h. Su velocidad de variación ${\tfrac {h}{t}}$ induce al mismo tiempo, según la segunda ecuación, un campo eléctrico abrazado al anterior. En el próximo y pequeño espacio de tiempo, este campo produce nuevamente, según la ecuación primera, un campo magnético que se abraza a él, y así se prolonga el proceso a modo de cadena con velocidad finita (fig. 93). Naturalmente es ésta una muy torpe descripción del proceso, que, en realidad, se extiende continuo en todas las direcciones; más tarde podremos bosquejar una imagen más adecuada.

fig93

Lo que nos interesa particularmente es lo siguiente: sabemos por la mecánica que la producción de una velocidad finita de propagación de ondas elásticas obedece a los retrasos que sobrevienen a consecuencia de la inercia de las masas, al trasladar las fuerzas de un punto a otro. La inercia de las masas, empero, es determinada por la aceleración, y ésta es la velocidad de variación de la velocidad; es $b={\tfrac {w}{t}}$, donde w es la variación de la velocidad $v={\tfrac {x}{t}}$ en el pequeño espacio de tiempo t. El retraso obedece, pues, por entero a la doble diferenciación.

Exactamente lo mismo sucede aquí; en primer término, la velocidad de variación ${\tfrac {e}{t}}$ del campo eléctrico determina el campo magnético H; luego la velocidad de variación ${\tfrac {h}{t}}$ de éste determina el campo eléctrico E en un lugar vecino. El progreso del campo eléctrico de lugar a lugar es, pues, condicionado por dos diferenciaciones temporales, esto es, por una formación totalmente análoga a la aceleración. Sobre este fundamento se apoya la existencia de ondas electromagnéticas. Si una de las acciones parciales transcurriese sin tiempo, no se verificarla una propagación de la fuerza eléctrica por ondas. Aquí se ve la importancia de la corriente de desplazamiento de Maxwell, pues ésta es justamente la velocidad de variación ${\tfrac {e}{t}}$ del campo eléctrico.

Ahora daremos una imagen de la propagación de una onda electromagnética, algo más aproximada a la realidad. Supongamos dos esferas metálicas cargadas con fuertes cargas contrarias +e y -e, de suerte que entre ellas exista un fuerte campo eléctrico; compénsanse entonces las cargas, el campo se deshace con gran velocidad de variación ${\tfrac {e}{t}}$. La figura muestra cómo se entrelazan sucesivamente lineas de fuerza eléctricas y magnéticas (fig. 94); las líneas de fuerza magnéticas hállanse dibujadas en el plano medio entre las esferas y las líneas de fuerza eléctricas en el plano del papel, que es perpendicular al anterior; la figura entera debe imaginarse, naturalmente, en rotación simétrica alrededor de la línea que une las esferas. Cada sinuosidad de las lineas de fuerza es más débil que la siguiente, porque está más hacia afuera y tiene mayor extensión; por eso la parte interna de una curva de fuerza eléctrica no suprime por completo la parte externa de la anterior, cuanto más que entra en acción con un pequeño retraso.

fig94

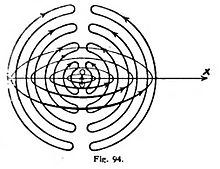
Si se sigue el proceso sobre una recta situada perpendicularmente a la linea de unión de los centros de las esferas, por ejemplo, a lo largo del eje x, se ve que sobre ésta las fuerzas eléctricas y magnéticas son siempre perpendiculares; y además son perpendiculares unas a otras. Lo mismo puede decirse, por lo demás, de toda dirección de propagación. La onda electromagnética es, pues, estrictamente transversal; es, además, polarizada; y aun cabe elegir el campo de fuerza eléctrico o el magnético para determinar el que da la pauta a la vibración.

No podemos demostrar aquí que la velocidad de propagación es precisamente igual a la constante c que se presenta en las fórmulas; pero es en sí muy plausible, pues sabemos que c tiene la dimensión de una velocidad. Como además, según Weber y Kohlrausch, la magnitud c es igual a la velocidad de la luz, pudo Maxwell concluir que las ondas luminosas no son sino ondas electromagnéticas.

De las consecuencias que Maxwell sacó, una fué pronto confirmada experimentalmente con cierta amplitud. Maxwell calculó la velocidad de la luz c₁ en un no-conductor no magnetizable notablemente (μ = 1, σ = 0); en tal caso, no puede depender, salvo de c, sino de la constante de dielectricidad ε, pues ésta es, para μ = 1, σ = 0, la única constante que aparece en las fórmulas [58]. Maxwell halló $c_{1}={\tfrac {c}{\sqrt {\varepsilon }}}$; de aquí se deriva, para el índice de refracción, $n={\tfrac {c}{c_{1}}}={\sqrt {\varepsilon }}$.

Así, pues, tenía que poderse determinar la refractabilidad de la luz por medio de la constante de dielectricidad, conocida por mediciones puramente eléctricas. Para algunos gases, como el hidrógeno, el óxido de carbono, el aire, es efectivamente el caso así, como lo ha demostrado L. Boltzmann (1874); para otras substancias, la relación de Maxwell $n={\sqrt {\varepsilon }}$ no es exacta; pero entonces el índice de refracción no es constante, sino que depende del color de la luz (número de vibraciones). Aquí aparece como causa de perturbación la dispersión de la luz; volveremos sobre esto desde el punto de vista de la teoría de los electrones. En todo caso, es claro que la constante de dielectricidad, medida estáticamente, coincidirá tanto mejor con el cuadrado del índice de refracción, cuanto más lentas sean las vibraciones o más largas las ondas de la luz empleada; vibraciones infinitamente lentas son idénticas a un estado estático. La moderna investigación de la esfera de las ondas largas en los rayos luminosos y térmicos, llevada a cabo por Rubens, ha dado por resultado una completa confirmación de la fórmula de Maxwell.

Por lo que se refiere a las leyes más geométricas de la óptica, la reflexión y refracción, la doble refracción y polarización en cristales, etc., desaparecen en la teoría electromagnética de la luz todas las dificultades, que para las teorías del éter elástico eran casi insuperables. La principal de esas dificultades era la existencia de ondas longitudinales que se presentan al atravesar la luz por las superficies-límites entre dos medios; esas ondas longitudinales no podían suprimirse a no ser estableciendo hipótesis muy inverosímiles sobre la constitución del éter. Pero las ondas electromagnéticas son siempre exactamente transversales. Así desaparece esa dificultad. Formalmente, la teoría de Maxwell es casi idéntica a la teoría del éter que formuló MacCullagh, como ya hemos dicho antes (IV, 6, página 125); puédese, sin nuevo cálculo, trasladar la mayor parte de sus deducciones.

No podemos seguir en detalle la ulterior evolución de la electrodinámica. El lazo de unión entre la luz y el electromagnetismo fué apretándose cada día más. Descubriéronse nuevos fenómenos que demuestran el influjo de los campos eléctricos y magnéticos sobre la luz. Todo se acomodaba a las leyes de Maxwell, cuya certeza crecía continuamente.

Pero la demostración decisiva de la unidad que junta la óptica con la electrodinámica fué dada por Heinrich Hertz (1888), demostrando la velocidad finita de propagación de la fuerza electromagnética y produciendo realmente ondas electromagnéticas. Entre dos esferas cargadas hizo saltar chispas, y produjo asi ondas como las que representa nuestro dibujo (figura 94). Cuando éstas entraban en un hilo metálico circular, que tenía una pequeña interrupción, producían en él corrientes que podían ser observadas merced a pequeñas chispas en la interrupción. Consiguió Hertz replegar esas ondas y hacerlas interferir; pudo así medir su longitud y su velocidad, que resultó ser exactamente la de la luz c. Así quedaba confirmada inmediatamente la hipótesis de Maxwell. Hoy las ondas hertzianas recorren la Tierra entre las grandes estaciones de telegrafía sin hilos y testimonian la grandesa de los dos investigadores Maxwell y Hertz, el primero de los cuales había predicho su existencia y el segundo llegó a hacerla realidad.

10. El éter electromagnético.

Desde ahora, ya no hay más que un solo éter, sustentáculo único de la totalidad de los fenómenos eléctricos, magnéticos, ópticos. Conocemos sus leyes, las ecuaciones de los campos de Maxwell; pero poco sabemos acerca de su constitución. ¿Qué es propiamente eso en que consisten los campos electromagnéticos, eso que verifica vibraciones en las ondas luminosas?

Recordamos que Maxwell fundaba sus consideraciones sobre el concepto del desplazamiento que hemos interpretado intuitivamente de manera que en las mínimas partículas o moléculas de éter, así como en las moléculas de la materia, se verifica un verdadero desplazamiento y separación de los flúidos eléctricos (o magnéticos). Esta representación, en lo que toca al proceso de la polarización eléctrica de la materia, está muy bien fundada y es admitida también por la nueva elaboración de la teoría de Maxwell, la teoría de los electrones. Pues innumerables experiencias han confirmado que la materia está constituida molecularmente y que cada molécula lleva cargas desplazables. Pero no sucede lo mismo para el éter libre; aquí el concepto de desplazamiento, de Maxwell, es puramente hipotético, y no tiene más valor que el de hacer intuitivas las leyes abstractas de los campos.

Estas leyes dicen que con todo desplazamiento variable en el tiempo está enlazada la producción de un campo electromagnético alrededor. ¿Es posible hacerse de esta conexión una imagen mecánica?

Maxwell mismo ha empleado con éxito heurístico modelos mecánicos para la constitución del éter. En esta dirección fué William Thomson (Lord Kelvin) particularmente rico en inventivas, esforzándose de continuo por comprender los fenómenos electromagnéticos como efectos de ocultos movimientos y fuerzas mecánicas.

El carácter rotativo de la conexión entre la corriente eléctrica y el campo magnético, y recíprocamente, invita a considerar el estado eléctrico del éter como desplazamiento lineal y el magnético como rotación alrededor de un eje, o inversamente.

Así se llega a representaciones que son afines a la teoría del éter establecida por MacCullagh; según éste, el éter no desarrollaba resistencias elásticas a contracciones en sentido corriente, sino resistencias a la rotación absoluta de sus elementos de volumen. Nos llevaría muy lejos enumerar las muchas hipótesis, a veces muy fantásticas, que se han hecho sobre la constitución del éter.

De tomarlas al pie de la letra, sería el éter una tremenda maquinaria de invisibles ruedas, palancas y encajes, que actúan en complicadísima manera, sin que de toda esta labor conozcamos nada más que algunas fuerzas relativamente sencillas que se manifiestan en la experiencia como campos electromagnéticos.

Hay también otras teorías más finas y a veces muy ingeniosas que consideran el éter como un flúido cuya velocidad de corriente es, por ejemplo, el campo eléctrico, y cuyos remolinos serían, en cambio, el campo magnético. Bjerknes ha bosquejado una teoría en la cual las cargas eléctricas son representadas como esferas que laten en el flúido etéreo, y ha mostrado que estas esferas ejercen unas sobre otras fuerzas que tienen una notable semejanza con las electromagnéticas.

Si inquirimos ahora el sentido y valor de tales teorías, hay que decir en su favor que han servido a veces, aunque raras, de estimulo para nuevos experimentos y descubrimientos de nuevos fenómenos. Pero muchas otras veces han inducido a grandes y penosas investigaciones experimentales, para decidir entre dos teorías del éter que eran ambas igualmente fantásticas e inverosímiles; de esta manera se ha desperdiciado absurdamente mucha labor. Todavía hay hoy gentes que consideran la explicación mecánica del éter electromagnético como una exigencia de la razón; siguen saliendo teorías que, naturalmente, son cada vez más abstrusas, pues la riqueza de los hechos a explicar, y por ende la dificultad del problema, aumenta de continuo.

Heinrich Hertz mantúvose conscientemente al margen de toda especulación mecanicista. Citemos sus propias palabras: «El interior de todos los cuerpos, incluidos en el libre éter, puede experimentar perturbaciones que designamos con el nombre de eléctricas, y otras perturbaciones que llamamos magnéticas. La esencia de esos cambios de estado no la conocemos; sólo conocemos los fenómenos que produce su presencia.» Esta renuncia clara a la explicación mecánica tiene una gran importancia metódica. Abre el camino para los grandes progresos que han sido alcanzados por los trabajos de Einstein. Las propiedades mecánicas de los sólidos y de los líquidos nos son conocidas por la experiencia; mas esta experiencia se refiere tan sólo a su conducta en lo grosero. Puede muy bien ser—y la moderna investigación molecular lo confirma— que esas propiedades visibles, groseras, sean una especie de apariencia, a que nos conduce engañosamente la torpeza de los métodos de observación; mientras que los procesos efectivos, entre los mínimos pilares de la construcción, átomos, moléculas y electrones, se verificarían por leyes muy distintas. Por eso es un prejuicio ingenuo el creer que todo medio continuo, como el éter, ha de conducirse de la manera como se conducen los flúidos y los sólidos, en apariencia continuos, del mundo sensible que se ofrece a nuestros torpes sentidos. Las propiedades del éter deben ser establecidas merced al estudio de los procesos que en él se verifican, independientemente de las demás experiencias. El resultado de estas investigaciones puede expresarse así: el estado del éter puede describirse por dos magnitudes dirigidas, que llevan los nombres de campos eléctricos y campos magnéticos E y H, y cuyas variaciones especiales y temporales están enlazadas por las ecuaciones de Maxwell; en ciertas circunstancias, el estado del éter condiciona acciones mecánicas, térmicas, químicas, sobre la materia, las cuales pueden llegar a ser observadas.

Todo lo que exceda de estas afirmaciones es hipótesis superflua, es fantasía. Se objetará que tal concepción abstracta encadena la inventiva del investigador, que necesita el estimulo de las imágenes intuitivas, de las analogías. Pero el ejemplo del mismo Hertz refuta este aserto; pues rara vez se han dado en un físico tanta inventiva experimental unida a tan pura abstracción de la teoría.

11. Teoría de Hertz sobre los cuerpos en movimiento.

Más importante que el pseudoproblema de la interpretación mecánica en los procesos del éter es la cuestión del influjo que tienen sobre los fenómenos electromagnéticos los movimientos de los cuerpos, entre los cuales hay que contar el éter fuera de la materia. Así volvemos, desde un punto de vista más general, a las investigaciones que antes hemos establecido acerca de la óptica de los cuerpos en movimiento (IV, 7-11). Ahora es la óptica una parte de la electrodinámica, y el éter luminoso es idéntico al éter electromagnético. Todas las conclusiones que hubimos de sacar de las observaciones ópticas acerca de la conducta que observa el éter luminoso deben conservar su validez, puesto que no dependen evidentemente del mecanismo de las vibraciones luminosas; nuestra investigación referíase sólo a los caracteres geométricos de una onda luminosa: número de vibraciones (efecto de Doppler), velocidad (arrastre) y dirección de la propagación (aberración).

Hemos visto que hasta la época en que se desarrolló la teoría electromagnética de la luz no habla asequibles a la medición mas que magnitudes del primer orden respecto de $\beta ={\tfrac {v}{c}}$. Y el resultado de esas observaciones pudo expresarse, en forma de «principio óptico de relatividad», de la manera siguiente: los procesos ópticos dependen solamente de los movimientos relativos de los cuerpos materiales, que en esos procesos participan, como focos luminosos, como medios de propagación, como cuerpos receptores; en un sistema de referencia movido en traslación verifícanse todos los procesos ópticos inferiores, como si el sistema permaneciese inmóvil en el éter.

Para explicar este hecho había dos teorías. La de Stokes admitía que el éter en el interior de la materia es totalmente arrastrado por ésta en su movimiento; la de Fresnel, en cambio, limitábase a admitir un arrastre parcial, cuya cantidad podía inferirse de ciertos experimentos. Hemos visto que la teoría de Stokes, desenvuelta con coherencia, tropieza con dificultades y, en cambio, que la de Fresnel expone satisfactoriamente todos los fenómenos.

En la teoría electromagnética son ambos puntos de vista posibles también: o un arrastre total, según Stokes, o uno parcial, según Fresnel. Se trata ahora de saber si por medio de observaciones puramente electromagnéticas puede conseguirse una decisión entre ambas hipótesis.

La hipótesis del arrastre total la aplicó primero Hertz sistemáticamente a las ecuaciones de los campos de Maxwell. Tenía Hertz plena conciencia de que tal manera de proceder sólo podía ser provisional, porque al hacer la aplicación a los procesos ópticos habrían de presentarse las mismas dificultades que dieron al traste con la teoría de Stokes; pero la sencillez de una teoría que no necesitaba distinguir entre el movimiento del éter y el de la materia le estimuló a desenvolverla y discutirla detenidamente. Demostróse entonces que los fenómenos de inducción en conductores en movimiento—que son los más importantes para la física experimental y la técnica—quedan reproducidos exactamente por la teoría de Hertz; pero las contradicciones con la experiencia se manifiestan tan pronto como se trata de experimentos más finos, en los cuales representan un papel los desplazamientos en cuerpos no-conductores. Vamos a investigar en serie todas las posibilidades:

1.° Conductor en movimiento.$\left\lbrace {\begin{matrix}\\\end{matrix}}\right.$	a) en el campo eléctrico.
	b) en el campo magnético.
2.° Aislador en movimiento. $\left\lbrace {\begin{matrix}\\\end{matrix}}\right.$	a) en el campo eléctrico.
	b) en el campo magnético.

fig95

1. a) Un conductor recibe en el campo eléctrico cargas superficiales. Si está en movimiento, las arrastra consigo; pero las cargas en movimiento deben ser equivalentes a una corriente, y, por tanto, producir, según la ley de Biot y Savart, un campo magnético. Para obtener una representación intuitiva, imaginemos un condensador cuyas placas son paralelas al plano xzc(fig. 95). Supongámoslas cargadas contrariamente y supongamos, además, que en la unidad de superficie de una placa existe la cantidad de electricidad e. Ahora una placa se mueve con respecto a la otra en la dirección x con la velocidad v; prodúcese entonces una corriente de arrastre o corriente de convección. La placa en movimiento recorre en la unidad de tiempo la longitud v; si su sección perpendicular al eje x es q, pasará por un plano paralelo al plano yz, en la unidad de tiempo, la cantidad de electricidad eqv, esto es, una corriente de densidad ev. Esta debe ejercer exactamente la misma acción magnética que una corriente conducida, que pasará por la placa inmóvil, con la densidad i = ev.

Esto fué confirmado experimentalmente en el laboratorio de Helmholtz por H. A. Rowland (1875) y luego más exactamente por A. Eichenwald (1903). En lugar de la placa movida en línea recta, empleóse un disco de metal en movimiento giratorio.

fig96

1. b) Si conductores se mueven en el campo magnético, prodúcense en ellos campos eléctricos y, por éstos, corrientes. Es ésta la inducción por movimiento, ya descubierta por Faraday e investigada cuantitativamente. El caso más sencillo es: el campo magnético H, producido, v. gr., por un imán en forma de herradura, es paralelo al eje z (figura 96); un trozo de hilo metálico recto es paralelo al eje y, y tiene la longitud 1 y es movido en la dirección x con la velocidad v. Resulta, según la teoría de Hertz, que en ese hilo es inducido un campo eléctrico paralelamente a la dirección negativa y; si se cierra el hilo por medio de un estribo que no toma parte en el movimiento, como indica la figura, correrá por él una corriente de inducción. Esto se demuestra sencillamente expresando del siguiente modo la ley de la inducción de Faraday: la corriente inducida en un hilo cerrado es proporcional a la variación por segundo del número de lineas de fuerza, o al desplazamiento μH, que es rodeado por el hilo. Por el movimiento del hilo aumenta evidentemente ese número en μHv por segundo; por lo cual el campo eléctrico inducido es igual a $\mu ;G{\tfrac {v}{c}}$.

Esta ley es el fundamento de todas las máquinas y aparatos de física y electrotécnica en los cuales por inducción transfórmase la energía de movimiento en energía electromagnética; entre éstos se hallan, por ejemplo, el teléfono, las dínamos de todas clases. La ley puede considerarse, pues, como comprobadísima y asegurada por innúmeros experimentos.

fig97

2. a) El movimiento de un no-conductor en un campo eléctrico podemos imaginarlo realizado del modo siguiente: entre las dos placas del condensador de la figura 95 se coloca un trozo movible hecho de material del no-conductor (fig. 97). Si el condensador se carga, prodúcese en el trozo un campo eléctrico E y un desplazamiento εE perpendicularmente al plano de las placas, esto es, paralelamente a la dirección y; así se cargan los dos planos límites del trozo aislador con igual pero opuesta electricidad, como la placa de metal que tienen enfrente. Sobre la cantidad de esa carga sabemos lo siguiente: en la página 190 hemos visto que la ley de Coulomb, según la concepción de Maxwell, pone la magnitud del desplazamiento, alrededor de una esfera cargada, en conexión con su carga e; para una esfera de radio e es a saber:

$E={\frac {e}{\varepsilon r^{2}}}$, o sea $\varepsilon E={\frac {e}{r^{2}}}$.

Mas esta esfera tiene la superficie 4πr², y la carga por unidad de superficie es, pues:

${\frac {e}{4\pi r^{2}}}={\frac {\varepsilon E}{4\pi }}$.

Traslademos esto al caso del condensador y tendremos que la densidad de la superficie en los planos límites de la placa aisladora será igual que en las placas metálicas y estará con el campo eléctrico E en la relación

$e={\frac {\varepsilon E}{4\pi }}$.

Si ahora la capa aisladora se mueve con la velocidad v en la dirección x, deberá el éter, según Hertz, ser arrastrado por completo en la capa; esto es, que también serán arrastrados el campo E y las cargas $e={\tfrac {\varepsilon E}{4\pi }}$, producidas por éste sobre los planos límites.

La carga en movimiento de una superficie límite representa, pues, una corriente de la densidad ${\tfrac {\varepsilon E}{4\pi }}v$, y deberá producir un campo magnético según la ley de Biot y Savart.

Que tal sucede, halo demostrado experimentalmente W. C. Roentgen (1885); pero la inclinación de la aguja magnética que él observó era mucho más pequeña de lo que debía ser según la teoría de Hertz. Se conduce, según las medidas de Röntgen, como si el aislador no arrastrase consigo todo el éter, sino sólo una parte. Pero la otra parte permanece inmóvil. Si el aislador fuera de éter puro, sería ε = 1 y la carga influenciada igual a ${\tfrac {E}{4\pi }}$; los experimentos de Röntgen demuestran que sólo el exceso de carga sobre ese valor, es decir,

${\frac {\varepsilon E}{4\pi }}-{\frac {E}{4\pi }}={\frac {E}{4\pi }}(\varepsilon -1)$,

toma parte en el movimiento de la materia. Este resultado lo interpretaremos más tarde sencillamente. Aquí baste establecer que, como era de esperar por los conocidos hechos de la óptica, la teoría de Hertz del arrastre total falla también en los puros procesos electromagnéticos.

Eichenwald ha confirmado (1903) el resultado de Röntgen, haciendo que las placas de metal cargadas tomasen parte en el movimiento. Estas dan una corriente de convección de la fuerza ev y la capa aisladora debería compensarla exactamente a causa de las cargas casi iguales y opuestas, según Hertz. Pero Eichenwald encontró que no es tal el caso; más bien obtuvo una corriente totalmente independiente de la materia del aislador. Esto mismo era de esperar, según el resultado de Röntgen sobre el arrastre parcial; pues la corriente procedente del aislador es $\left({\tfrac {\varepsilon E}{4\pi }}-{\tfrac {E}{4\pi }}\right)v$, y el primer miembro de la misma es compensado por la corriente de convección ev y queda la corriente ${\tfrac {E}{4\pi }}v$, que es independiente de la constante de dielectricidad ε.

fig98

2. b) Imaginemos un campo magnético paralelo al eje z, realizado, v. gr., por un imán de herradura, y un trozo de materia no conductora moviéndose por el campo en la dirección x (fig. 98). Como no hay no-conductores que sean magnetizables (perceptiblemente), admitiremos μ = 1. Los dos planos límites del trozo aislador, que sean perpendiculares al eje y, cubrámoslos de metal; estas cubiertas metálicas estarán unidas a un electrómetro, de modo que pueda medirse la carga que se produzca en ellas.

Este experimento corresponde exactamente al experimento de inducción explicado en 1 b), sólo que, en lugar del conductor en movimiento, se pone un dieléctrico en movimiento. La ley de inducción puede aplicarse de la misma manera; exige la existencia de un campo eléctrico E = vH actuando en la dirección negativa y, si la espesura del trozo aislador es igual a 1. Por eso, según la teoría de Hertz, las dos cubiertas metálicas deben presentar cargas opuestas con la densidad de superficie ${\tfrac {\varepsilon E}{4\pi }}={\tfrac {\varepsilon vH}{4\pi }}$, que provocan una oscilación del electrómetro. El experimento fué dispuesto en 1905 por H. A. Wilson (con un dieléctrico girando), y confirmó la existencia de la carga; pero también en menor cantidad, esto es, correspondiendo a una densidad de superficie $(\varepsilon -1){\tfrac {vH}{4\pi }}$. De nuevo parece conducirse como si no tomase parte todo el éter en el movimiento de la materia sino sólo en la cantidad en que ésta es más fuerte dieléctricamente que el vacío. También aquí falla la teoría de Hertz.

En estos cuatro fenómenos típicos, refiérese todo evidentemente al movimiento relativo de los cuerpos productores de campos respecto del conductor o aislador que se investiga. En lugar de mover éste en la dirección x, como ya hemos hecho, podría mantenerse inmóvil y mover las demás partes del aparato en la dirección negativa x; el resultado tendría que ser el mismo. La teoría de Hertz no conoce sino movimientos relativos de los cuerpos, valiendo el éter como tal cuerpo. En un sistema animado de un movimiento de traslación, todos los procesos suceden, según Hertz, como si el sistema se mantuviese inmóvil; rige, pues, el principio clásico de relatividad.

Pero la teoría de Hertz es inconciliable con los hechos, y hubo de dejar el puesto a otra que, con respecto a la relatividad, adoptó exactamente el punto de vista contrario.

12. La teoría de los electrones de Lorentz.

Es la teoría de H. A. Lorentz (1892), que significó el punto culminante y la conclusión de la física del éter substancial.

Es una teoría de la electricidad desarrollada en sentido atomístico y en el de un solo flúido; por lo cual queda también, como en seguida veremos, determinado el papel que le atribuye al éter.

Helmholtz (1881) es el primero que ha expuesto que las cargas eléctricas tienen una estructura atomística, se presentan en magnitudes pequeñas e indivisibles; hízolo para hacer inteligibles las leyes de la electrólisis de Faraday (pág. 178). En realidad, basta admitir que cada átomo en la solución electrolítica verifica una especie de unión química con un átomo de electricidad, o electrón, para comprender que una determinada cantidad de electricidad produzca la división o descomposición de siempre equivalentes cantidades de substancia.

La atomística eléctrica se distinguió, sobre todo, en la explicación de los fenómenos que se observan al pasar la corriente eléctrica por un gas rarificado.

fig99

Descubrióse primero que la electricidad positiva y la negativa se conducen por modo completamente distinto. Si en un tubo de vidrio se introducen dos electrodos de metal y se hace pasar una corriente por ellos (figura 99), obtiénense muy complicados fenómenos, mientras haya en el tubo gas de observable presión; pero si se quita gas poco a poco, la imagen va haciéndose más sencilla. En llegando a altísimo vacío, sale del electrodo negativo, el cátodo K, un rayo de luz azulada en línea recta, sin preocuparse lo más mínimo de donde se encuentra el polo positivo, el ánodo A. Estos rayos catódicos, que descubrió Pluecker en 1858, fueron considerados por muchos como ondas luminosas, pues producían, como Hittorf demostró (1869), sombras de los cuerpos sólidos que se ponían en su camino; otros los consideraron como emanación material acelerada por el cátodo. Crookes, que representaba este punto de vista (1879), llamó a los rayos el «cuarto estado de agregación» de la materia. En favor de la naturaleza material de los rayos, testimoniaba principalmente a circunstancia de que son desviados por un imán, y lo son justamente como corriente de electricidad negativa. En la investigación de la naturaleza de los rayos catódicos han tomado la mayor parte J. J. Thomson y Ph. Lenard. Se consiguió demostrar la carga negativa de los rayos por captación directa; también son desviados por un campo eléctrico que se acerque de lado a su trayectoria, y ello contrariamente a la dirección del campo, lo cual demuestra una vez más su carga negativa.

La convicción de que los rayos catódicos eran de naturaleza corpuscular se abrió paso cuando se consiguió sacar conclusiones cuantitativas sobre su velocidad y su carga.

fig100

Representémonos el rayo catódico como una corriente de partículas, de masa m; en tal caso será desviado por un determinado campo eléctrico o magnético, tanto menos cuanto mayor sea su velocidad; así como una bala de fusil corre tanto más recta cuanto más rápida. Ahora bien; pueden producirse rayos catódicos muy desviables, esto es, muy lentos; pueden, artificialmente, acelerarse tanto que su velocidad inicial, comparada con su velocidad final, puede, despreciarse. Para ello se coloca delante del cátodo K una red de hilos metálicos (figura 100) cargada positivamente con fuerte carga; entonces las partículas negativas de los rayos catódicos son fuertemente aceleradas en el campo entre el cátodo y la red metálica, y pasan por las mallas de la red con una velocidad que esencialmente procede de esa aceleración. Esta, empero, puede calcularse según la ecuación fundamental de la mecánica

$mb=K=eE$,

siendo e la carga y E el campo; se tiene evidentemente un «movimiento de caída», en el cual la aceleración no es igual a la aceleración de la gravedad g, sino igual a ${\tfrac {e}{m}}E$. Si fuese conocida la relación ${\tfrac {e}{m}}$, podría hallarse la velocidad v por medio de las leyes de la caída. Pero tenemos dos incógnitas, ${\tfrac {e}{m}}$ y v, y necesitamos una medición más para determinarlas. Esta se consigue empleando un campo magnético lateral. Al hablar de la teoría de Hertz (V, 11, 1 b, pág. 215), hemos visto que un campo magnético H en un cuerpo que se mueve perpendicularmente a H produce un campo eléctrico $E={\tfrac {v}{c}}H$, que es perpendicular tanto a H como a v. Por lo tanto, sobre cada partícula del rayo catódico actuará una fuerza desviante $eE=e{\tfrac {v}{c}}H$, de suerte que se produce perpendicularmente al primitivo movimiento una aceleración $b={\tfrac {ev}{mc}}H$. Esta puede hallarse midiendo la desviación lateral del rayo; tenemos, pues, una segunda ecuación para determinar las incógnitas ${\tfrac {e}{m}}$ y v.

Las determinaciones obtenidas por este método u otro semejante han dado por resultado que para velocidades no demasiado grandes, ${\tfrac {e}{m}}$ tiene, efectivamente, un valor determimnado, constante, que

${\frac {e}{m}}=5,31\cdot 10^{17}$

unidades electrostáticas de carga por gramo. Por otra parte, al hablar de la electrólisis (pág. 181), hemos indicado que 1 g. de hidrógeno transporta la cantidad de electricidad C₀ = 2,90 · 10¹⁴. Si ahora se admite que la carga de una partícula es en ambos casos la misma, es decir, un átomo de electricidad o electrón, hay que concluir que la masa m de la partícula del rayo catódico es al átomo de hidrógeno m_H como

${\frac {m}{m_{H}}}={\frac {e}{m_{H}}}:{\frac {e}{m}}={\frac {2,90\cdot 10^{14}}{5,31\cdot 10^{17}}}={\frac {1}{1830}}$

Las partículas de los rayos catódicos son, pues, unas dos mil veces más ligeras que los átomos de hidrógeno, que, por su parte, son los más ligeros de todos los átomos. Este resultado hace plausible la conclusión de que en los rayos catódicos tenemos una corriente de átomos eléctricos puros.

Esta concepción se ha visto confirmada por innumerables investigaciones. La electricidad negativa consiste en los electrones libremente movibles; la positiva, empero, está adherida a la materia y no se presenta nunca sin ésta. La moderna investigación experimental ha confirmado así y precisado la hipótesis de la antigua teoría de un flúido. También se ha conseguido determinar la cantidad de la carga e del electrón. Los primeros experimentos de esta clase los emprendió J. J. Thomson en 1898. La idea fundamental es ésta: las pequeñas gotas de aceite, agua o esferitas de metal de dimensiones microscópicas o submicroscópicas, que se producen por condensación de vapor o por dispersión en el aire, caen con velocidad constante, porque el frotamiento del aire impide que se produzcan aceleraciones. Puede determinarse la magnitud de las partículas midiendo la velocidad de caída, y su masa M, multiplicando por la densidad. El peso de una de esas partículas es entonces Mg, siendo g=981 cm./sec.² la aceleración de la Tierra. Ahora bien; pueden cargarse eléctricamente tales partículas sometiendo el aire a la acción de rayos Röntgen o rayos de substancias radioactivas. Si se acerca luego un campo eléctrico E, dirigido verticalmente hacia adelante, resultará que una esferita de carga e será tirada hacia arriba por el campo, y si la fuerza eléctrica eE es igual al peso Mg, flotará. Por la ecuación eE = Mg puede calcularse la carga e. Millikan (1910), que ha hecho los más precisos experimentos de esta especie, ha encontrado que la carga de pequeñas gotas es siempre un múltiplo entero de una determinada pequeñísima carga; ésta podrá llamarse el quantum eléctrico elemental. Su magnitud es:

$e=4,77\cdot 10^{-10}{\text{unidades electrostáticas}}$.

Sin duda, los experimentos de Millikan son criticados por Ebrenhaft; sin embargo, es verosímil que los valores más bajos que éste ha hallado de la carga elemental obedecen a haber operado con esferas demasiado pequeñas, en las cuales se producen fenómenos secundarios.

Para la teoría electrónica de Lorentz no representa ningún papel esencial la magnitud absoluta de la carga elemental. Vamos ahora a describir la imagen del mundo físico tal como Lorentz la ha bosquejado.

Los átomos materiales son los portadores de la electricidad positiva, que está inseparablemente unida a ellos; pero, además, contienen un gran número de electrones negativos, de suerte que hacia afuera parecen eléctricamente neutros. En los no conductores, los electrones están firmemente unidos a los átomos; pueden solamente ser algo desviados de sus posiciones de equilibrio, por donde el átomo se transforma en dípolo. En los electrólitos y en los gases conductores sucede que un átomo tiene un electrón o varios electrones de más o de menos; entonces se llama ion o portador y viaja en el campo eléctrico, transportando a la vez electricidad y materia. En los metales muévense los electrones libremente, y sólo por choques con los átomos de la substancia experimentan una resistencia. Prodúcese el magnetismo porque en ciertos átomos los electrones dan vueltas en trayectorias cerradas, y así representan corrientes moleculares de Ampere.

Los electrones y las cargas positivas atómicas nadan en el mar del éter, en el cual existe un campo electromagnético conforme a las ecuaciones de Maxvell; pero en este es ε = 1 y μ = 1, y en lugar de la densidad de la corriente conducida, preséntase la corriente de convección de los electrones ρv. Las ecuaciones de Maxvell dicen, pues:

${\begin{cases}{\text{div.}}E=\rho ,\quad &{\text{rot.H}}-{\frac {1}{c}}{\frac {e}{t}}={\frac {\rho v}{c}},\\{\text{div.}}H=0,\quad &{\text{rot.E}}+{\frac {1}{c}}{\frac {h}{t}}=0,\end{cases}}$[61]

y comprenden las leyes de Coulomb, Biot, Savart y Faraday en la manera ya conocida.

Todos los procesos electromagnéticos consisten, pues, en el fondo, en los movimientos de electrones y los campos que les acompañan. La materia toda es un fenómeno eléctrico. Las diferentes propiedades de la materia obedecen a las diferencias de movilidad de los electrones con respecto a los átomos, como acabamos de describirlas. La teoría electrónica debe ahora resolver el problema que consiste en deducir de las leyes fundamentales para los invisibles electrones y átomos [61] las ecuaciones corrientes de Maxvell, es decir, mostrar que los cuerpos materiales, según su naturaleza, parecen tener una capacidad conductora σ, una constante de dielectricidad ε y una permeabilidad μ.

Lorentz ha resuelto este problema y ha mostrado que la teoría electrónica no sólo da las leyes de Maxvell en el caso más sencillo, sino que, además, hace posible la explicación de numerosos detalles que no eran accesibles a la teoría descriptiva o que sólo lo eran merced a hipótesis artificiosas. Entre esos detalles cuéntanse, sobre todo, los delicados fenómenos de la óptica, la dispersión de los colores, la rotación magnética del plano de polarización descubierta por Faraday (véase pág. 204) y otras acciones recíprocas entre las ondas luminosas y los campos eléctricos o magnéticos. No podemos seguir en detalle esta amplísima teoría, llena de complicaciones matemáticas. Nos limitaremos a este problema, que es el que nos interesa sobre todo: ¿qué parte toma el éter en el movimiento de la materia?

Lorentz establece una afirmación radicalísima, que no se había manifestado nunca con tal precisión.

El éter permanece absolutamente inmóvil en el espacio.

Así quedan, en principio, identificados totalmente el espacio absoluto y el éter. El espacio absoluto no es un vacío, sino algo que posee propiedades determinadas y cuyo estado se describe indicando dos magnitudes dirigidas, el campo eléctrico E y el campo magnético H; como tal, el espacio absoluto se llama éter.

Esta hipótesis va algo más allá que la teoría de Fresnel. Según éste, el éter del espacio cósmico estaba inmóvil en un sistema inercial, por lo cual podía decirse que estaba en inmovilidad absoluta; pero el éter, dentro de los cuerpos materiales, es en parte arrastrado por éstos.

fig101

Lorentz puede renunciar también a ese arrastre parcial de Fresnel y llega, sin embargo, prácticamente al mismo resultado. Para comprenderlo, consideremos el proceso dentro de un dieléctrico entre las placas de un condensador. Si éste es cargado, prodúcese un campo perpendicular a las placas (fig. 101), y éste desplaza los electrones en los átomos de la substancia dieléctrica y los transforma en dípolos, tal como lo hemos explicado ya (páginas 191 y 197). El desplazamiento dieléctrico en el sentido de Maxvell es εE; pero sólo una parte del mismo procede del desplazamiento efectivo de los electrones, pues el vacío tiene la constante de dielectricidad ε = 1; es decir, el desplazamiento E; por consiguiente, la parte que en el desplazamiento tienen los electrones es solamente εE - E = (ε - 1)E. Pero ya hemos visto que los experimentos de Röntgen y Wilson, sobre los fenómenos en aisladores movidos, dicen que, efectivamente, sólo esa parte del desplazamiento participa en el movimiento. La teoría de Lorentz expone, pues, exactamente los hechos electromagnéticos, sin necesidad de que el éter tome parte en el movimiento de la materia.

El arrastre de la luz resulta también conforme con la fórmula de Fresnel [39] (pág. 156); esto se ve de la siguiente manera: Consideremos, como en el experimento de Wilson, un cuerpo dieléctrico que se mueve, en la dirección x, con la velocidad v, y en el cual un rayo de luz corre en la misma dirección (figura 102). Este consiste en una vibración eléctrica E paralela al eje y y en otra magnética paralela al eje z. Pero ya sabemos, por el experimento de Wilson, que tal campo magnético produce en el cuerpo en movimiento un desplazamiento eléctrico suplementario en la dirección y, del valor de (ε — 1) de donde se obtiene un campo eléctrico suplementario por división por ε. El campo eléctrico total es, pues:

$E+{\frac {\varepsilon -1}{\varepsilon }}vH$.

fig102

Si el arrastre fuese total, como supone la teoría de Hertz, tendríamos ε en lugar de ε — 1; esto es, que el campo total tendría la magnitud E + vH. Se ve que, a causa del arrastre parcial, hay que substituir v por

${\frac {\varepsilon -1}{\varepsilon }}v$.

Esta magnitud debería, pues, corresponder a la velocidad absoluta del éter dentro de la materia, según la teoría de Fresnel, es decir, al número de arrastre designado en la óptica con φ, fórmula [39]. Y efectivamente es así; pues, según la teoría de la luz, dada por Maxwell (pág. 207), es la constante de dielectricidad ε igual al cuadrado del índice de refracción n, ε = n². Inclúyase esta igualdad en la fórmula y se obtiene:

${\frac {\varepsilon -1}{\varepsilon }}v={\frac {n^{2}-1}{n^{2}}}v=\left(1-{\frac {1}{n^{2}}}\right)v=\varphi .$

en concordancia con la fórmula [39] (pág. 156).

Recordemos que la teoría de Fresnel tropezaba con dificultades procedentes de la dispersión de los colores. Pues si el índice de refracción n depende de la frecuencia (color) de la luz, también dependerá de ella el número del arrastre φ; pero el éter no puede ser arrastrado mas que de una manera determinada, y no de distinto modo para cada color. Esta dificultad desaparece en la teoría de los electrones, pues el éter permanece inmóvil, y los que son arrastrados son los electrones residentes en la materia; y entonces la dispersión de los colores obedece a que los electrones son llevados por la luz a vibrar con ella y retroactivamente influyen en la velocidad de la luz.

No podemos seguir los detalles de esta teoría llena de ramificaciones. Compendiaremos el resultado.

La teoría de Lorentz supone la existencia de un éter absolutamente inmóvil; además, demuestra que, a pesar de ello, todos los fenómenos ópticos y electromagnéticos dependen sólo de los movimientos relativos de traslación que verifican los cuerpos materiales, en cuanto que se consideran miembros del primer orden en β. Explica, pues, todos los procesos conocidos y, sobre todo, el hecho de que el movimiento absoluto de la Tierra a través del éter no es observable por experimentos terrestres con respecto a magnitudes del primer orden (principio óptico, o mejor electromagnético, de la relatividad).

Pero cabe imaginar un experimento (primer orden) que no podría explicarse por la teoría de Lorentz, como tampoco por ninguna de las anteriores teorías del éter; sería un fracaso del método de Römer para el establecimiento de un movimiento absoluto de todo el sistema solar (véanse páginas 147 y 164).

Será decisivo para la teoría de Lorentz el decidir si podrá o no mantenerse ante experimentos que permitan medir magnitudes del segundo orden en β. Pues tales experimentos habrían de establecer el movimiento absoluto de la Tierra por el éter. Pero antes de llegar a este problema hemos de hablar de un resultado de la teoría electrónica de Lorentz, por el cual ha ampliado grandemente su esfera: la interpretación electrodinámica de la inercia.

13. La masa electromagnética.

Le habrá extrañado al lector que, desde el momento en que hemos abandonado el éter elástico para ocuparnos del electrodinámico, ya hemos hablado poco de mecánica. Los procesos mecánicos y los procesos electromagnéticos forman cada uno por sí un reino; los primeros se verifican en el espacio absoluto de Newton, que queda definido por la vigencia de la ley de inercia y que da a conocer su existencia en las fuerzas centrifugas; los segundos son estados del éter inmóvil en el espacio absoluto. Una teoría comprensiva y amplia, como quiere ser la de Lorentz, no puede dejar esos dos reinos uno junto a otro, sin un enlace que los una.

Hemos visto ya que una reducción de la electrodinámica a la mecánica no se ha conseguido satisfactoriamente, a pesar del esfuerzo tremendo que han aplicado a ello investigadores sutilísimos.

Preséntase el audaz pensamiento inverso: ¿no podrá reducirse la mecánica a la electrodinámica?

Si ello se consiguiese, el espacio abstracto absoluto de Newton quedaría convertido en el éter concreto; las resistencias de inercia y las fuerzas centrifugas deberían aparecer como acciones físicas del éter; por ejemplo, como campos electromagnéticos de configuración especial. Pero entonces el principio de relatividad de la mecánica habría de perder su estricta validez y quedaría reducido, como el de la electrodinámica, a una vigencia aproximada, para magnitudes del primer orden en $\beta ={\tfrac {v}{c}}$.

La ciencia no ha retrocedido ante ese paso, que revoluciona el orden de los conceptos. Y aunque la teoría del éter absolutamente inmóvil ha tenido que caer más tarde, sin embargo, esta revolución, que destrona la mecánica y establece el dominio de la electrodinámica sobre la física toda, no ha sido vana: su resultado conserva validez en una forma algo alterada.

Ya hemos visto (pág. 205) que la propagación de ondas electromagnéticas se produce porque la acción reciproca de los campos eléctricos y magnéticos provoca un efecto análogo a la inercia mecánica. Un campo electromagnético tiene una facultad de permanencia muy semejante a una masa mecánica; para producirlo, hay que emplear trabajo, y cuando se aniquila reaparece ese trabajo empleado. Ello se ve en todos los procesos que van unidos a vibraciones electromagnéticas, por ejemplo, en los aparatos de telegrafía sin hilos. Una estación radiotelegráfica tiene un oscilador eléctrico, que consiste esencialmente en un espacio de chispa F, una bobina S y un condensador K; esto es, dos placas de metal aisladas una de otra, las cuales, unidas por hilos, forman un circulo de corriente «abierta» (fig. 103). Se carga el condensador hasta que en F salta una chispa; el condensador entonces se descarga, y las cantidades de electricidad almacenadas se desprenden. Pero no se compensan sencillamente, sino que disparan sobre el equilibrio y se reúnen de nuevo en las placas del condensador, aunque con signo contrario, como un péndulo, al oscilar, pasa por la posición de equilibrio y sigue hacia el lado opuesto. Terminada la nueva carga del condensador, corre la electricidad de nuevo y oscila como un péndulo hasta que su energía se gasta por calentamiento de los hilos conductores o por desgaste de otras partes del aparato; v. gr., de las antenas irradiantes. La oscilación de la electricidad demuestra, pues, la capacidad de permanencia que posee el campo, lo cual corresponde exactamente a la inercia de masa en la bola del péndulo. La teoría de Maxvell expone este hecho en todos sus detalles con exactitud; las oscilaciones electromagnéticas, que se presentan en un determinado aparato, pueden calcularse de antemano por medio de las ecuaciones de los campos.

fig103

J. J. Thomson sacó de aquí la conclusión de que la inercia de un cuerpo puede aumentarse dándole una carga eléctrica. Consideremos una esfera cargada, primero inmóvil y luego en movimiento con la velocidad v. La esfera inmóvil tiene un campo electrostático con líneas de fuerza radiales; la esfera en movimiento tiene, además, un campo magnético con líneas de fuerza circulares que envuelven la trayectoria de la esfera (fig. 104); pues una carga en movimiento es una corriente de convección y produce un campo magnético según la ley de Biot y Savart. Ambos estados tienen la facultad de permanencia que hemos descrito; el uno no puede transformarse en el otro sino por un gasto de trabajo. La fuerza necesaria para poner la esfera inmóvil en movimiento es, pues, para la esfera cargada, mayor que para la no cargada. Para acelerar la esfera ya en movimiento debe reforzarse evidentemente el campo magnético H; pero es, pues, necesaria una mayor fuerza.

fig104

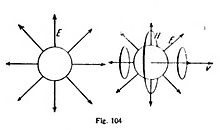
Recordaremos que una fuerza K actuando durante un breve tiempo t, representa un impulso J = Kt, que produce una variación de velocidad w de una masa m, según la fórmula [6] (II, 9, pág. 47):

$mw=J$.

Si la masa lleva una carga, una impulsión determinada J producirá una variación de velocidad más pequeña, y el resto, J', se gastará en variar el campo magnético; será, pues:

$mw=J-J'$

El cálculo da el muy plausible resultado de que la impulsión J' necesaria para aumentar el campo magnético es tanto mayor cuanto mayor sea la variación de velocidad w; y es aproximadamente proporcional a ella. Puede, pues, ponerse J' = m'w, siendo m' un factor de proporcionalidad que, por lo demás, puede depender de la velocidad v anterior a la variación de velocidad. Entonces tendremos:

$mw=J-m'w$,

o sea:

$(m+m')w=J$

Es, pues, como si la masa m quedase aumentada en una cantidad m', que podrá calcularse por las ecuaciones de los campos electromagnéticos; esa cantidad m' puede depender también de la velocidad v. El valor exacto de m', para cualesquiera velocidades v, sólo puede calcularse haciendo hipótesis sobre la distribución de la carga eléctrica en el cuerpo en movimiento. Pero el valor límite para velocidades pequeñas relativamente a la velocidad de la luz c, es decir, para pequeñas β, se manifiesta independiente de tales hipótesis:

$m_{e}={\frac {4}{3}}{\frac {U}{c^{2}}}$,[62]

siendo U la energía electrostática de las cargas del cuerpo.

Ya hemos visto que la masa del electrón es unas dos mil veces menor que la del átomo de hidrógeno. Se ofrece la idea de que el electrón acaso no tenga una masa «ordinaria», sino que no sea otra cosa que «carga eléctrica» en si, y que su masa sea de origen puramente electromagnético.

¿Es tal hipótesis conciliable con los conocimientos que tenemos acerca de la magnitud, carga y masa del electrón?

Como los electrones han de ser como los pilares de que están hechos los átomos, resultarán desde luego, pequeños comparados con la magnitud de los átomos. Ahora bien; por la física atómica es sabido que el radio de los átomos es del orden 10^-8 cm.; el radio del electrón deberá ser mucho más pequeño que 10^-8 cm. Si nos representamos el electrón como una esfera de radio a, con la carga e distribuida por su superficie, la ley de Coulomb nos permite inferir que la energía electrostática es $U={\tfrac {1}{2}}{\tfrac {e^{2}}{a}}$; por donde la masa electromagnética será, según la fórmula [62],

$m_{e}={\frac {4}{3}}{\frac {U}{c^{2}}}={\frac {1}{2}}{\frac {e^{2}}{ac^{2}}}$.

Podemos, pues, calcular el radio a:

$a={\frac {2}{3}}\cdot {\frac {e}{c^{2}}}\cdot {\frac {e}{m_{e}}}$.

En el lado derecho todo es conocido: ${\tfrac {e}{m_{e}}}$ lo es por la desviación de los rayos catódicos (pág. 221); e lo es por las mediciones de Millikan (pág. 223), y c es la velocidad de la luz. Si se ponen los valores numéricos de cada letra, tendremos:,

$a={\frac {2}{3}}\cdot {\frac {4,77\cdot 10^{-10}}{9\cdot 10^{20}}}\cdot 5,31\cdot 10^{17}=1,88\cdot 10^{-12}{\text{cm.,}}$

longitud que es, aproximadamente, cien mil veces menor que el radio del átomo.

La hipótesis de un origen puramente electromagnético de la masa del electrón no está, pues, en contradicción con los hechos conocidos. Pero no por ello está aún demostrada.

La teoría halló vigorosa ayuda en delicadas observaciones hechas sobre los rayos catódicos y los rayos β de substancias radioactivas, los cuales son igualmente electrones expelidos. Ya hemos explicado que, influenciando esos rayos eléctrica y magnéticamente, puede determinarse tanto la relación de carga a masa ${\tfrac {e}{m}}$ como también la velocidad v, y que para ${\tfrac {e}{m}}$ fué hallado primero un valor determinado independiente de v. Pero, al pasar luego a mayores velocidades, hallóse una diminución de ${\tfrac {e}{m}}$; principalmente en los rayos β del radio, que son poco más lentos que la luz, fué muy claro este efecto, y pudo ser medido en cantidad. Que la carga eléctrica deba depender de la velocidad era cosa inconciliable con las representaciones de la teoría electrónica. Pero podía esperarse muy bien que la masa dependiera de la velocidad, si ésta es de origen electromagnético. Para llegar a una teoría cuantitativa había que hacer desde luego determinadas hipótesis sobre la forma del electrón y la distribución de la carga en él. M. Abraham (1903) consideró el electrón como esfera rígida con una carga uniformemente repartida sobre el interior o la superficie, y mostró que ambas hipótesis conducen a establecer igualmente que la masa electromagnética depende de la velocidad, en el sentido de que aumenta la masa al aumentar la velocidad. Cuanto más rápidamente corre el electrón, tanto más resiste el campo electromagnético a una posterior variación de velocidad. El aumento de m explica la disminución observada de ${\tfrac {e}{m}}$ y la teoría de Abraham concuerda muy bien cuantitativamente con los resultados de las mediciones hechas por Kaufmann (1901), si se admite que no existe ninguna masa «ordinaria» junto a la masa electromagnética.

Llegábase, pues, al fin propuesto: reducir la inercia de los electrones a campos electromagnéticos en el éter. Al mismo tiempo abríase una perspectiva amplia. Como los átomos son los portadores de la electricidad positiva y además contienen numerosos electrones, ¿no será acaso su masa también de origen electromagnético? En tal caso, la masa, como cantidad de la facultad de permanecer, no sería un fenómeno primario, como lo es en la mecánica elemental, sino una consecuencia secundaria de la estructura del éter. El espacio absoluto de Newton, que se define solamente por la ley mecánica de inercia, resulta así innecesario; su papel lo desempeña el éter, bien conocido ya por sus propiedades electromagnéticas. De este modo habríase conseguido una solución muy concreta del problema del espacio, muy acorde con el pensar físico.

Ya veremos (V, 15, pág. 240) que nuevos hechos han venido a contradecir esta concepción; pero la conexión entre la masa y la energía electromagnética, que fué descubierta entonces por vez primera, significa un conocimiento fundamental, cuyo profundo sentido ha recibido su recta validez en la teoría de la relatividad de Einstein.

Aun debemos añadir que, además de la teoría del electrón rígido de Abraham, hanse establecido y calculado otras hipótesis. La más importante es la de Lorentz (1904), en estrecha relación con la teoría de la relatividad. Lorentz admitió que el electrón, al moverse, se contrae en la dirección del movimiento, y de esfera se transforma en elipsoide de revolución; la cantidad del aplastamiento dependería, por modo determinado, de la velocidad. Esta hipótesis parece al pronto muy extraña; desde luego, da una fórmula mucho más sencilla que la de la teoría de Abraham, para la masa electromagnética en su dependencia de la velocidad. Pero no seria esto una justificación suficiente. Esta justificación se encuentra mejor fundada en la evolución que hubo de seguir la teoría electrónica de Lorentz, a consecuencia de las investigaciones experimentales sobre las cantidades del segundo orden, de las cuales vamos a ocuparnos en seguida. La fórmula de Lorentz para la masa del electrón ha recibido después en la teoría de la relatividad un sentido universal; más tarde volveremos sobre la decisión experimental entre ella y la teoría de Abraham (VI, 7, pág. 288).

Cuando la teoría electrónica, al término del siglo xix, hubo llegado al estado que hemos descrito, parecía muy próxima la posibilidad de una imagen unitaria del mundo físico que redujese todas las formas de la energía, incluso la inercia mecánica, al campo electromagnético en el éter. Una sola forma de energía permanecía fuera del sistema: la gravitación; pero podía esperarse que también ésta lograría ser considerada como acción del éter.

14. El experimento de Michelson.

Pero ya veinte años antes, el fundamento del edificio entero había subido de un salto, y al mismo tiempo que ascendía la construcción, hacíase preciso apuntalar y reforzar la base.

Ya hemos insistido varias veces en que para la teoría del éter inmóvil habían de ser decisivos los experimentos que consiguieran medir magnitudes del segundo orden en β; en éstas debía, en efecto, manifestarse si sobre un cuerpo que se mueve rápidamente actúa el viento de éter, empujando las ondas luminosas, como así lo exige la teoría.

El primero y más importante experimento de esta clase consiguió realizarlo Michelson (1881) con su interferómetro (IV, 4, pág. 119), que, merced a un trabajo infatigable, logró perfeccionar hasta hacer de él un instrumento de precisión capaz de inauditas verificaciones.

En la investigación del influjo que el movimiento de la Tierra pueda tener sobre la velocidad de la luz (IV, 9, pág. 151) se ha visto que el tiempo que necesita un rayo luminoso para recorrer de ida y vuelta una distancia l, paralela a la trayectoria terrestre, difiere sólo por una magnitud del segundo orden del valor que tendría estando la Tierra inmóvil; allí encontramos antes para el tiempo ése la expresión siguiente:

$t_{1}=l\left({\frac {1}{c+v}}+{\frac {1}{c-v}}\right)={\frac {2lc}{c^{2}-v^{2}}}$,

que puede escribirse también:

$t_{1}={\frac {2l}{c}}\cdot {\frac {1}{1-\beta ^{2}}}$.

Si se pudiera medir ese tiempo con exactitud tal que hubiera la certeza de distinguir la fracción ${\tfrac {1}{1-\beta ^{2}}}$ de 1, a pesar del pequeñísimo valor de β², ése seria un medio para demostrar el viento de éter.

fig105

Pero los tiempos luminosos en sí no pueden medirse con tamaña exactitud; los métodos interferométricos no dan sino diferencias de los tiempos que necesita la luz en diferentes caminos, con aquella enorme exactitud que es necesaria para el fin propuesto.

Por eso Michelson hace que un segundo rayo luminoso recorra de ida y vuelta un camino AB de la misma longitud l, pero perpendicular a la trayectoria terrestre (fig. 105). Mientras la luz va de A a B, la Tierra se ha movido un poquito hacia adelante, de suerte que el punto B ocupa ahora el lugar B' del éter; el verdadero camino de la luz en el éter es, pues, AB', y si para recorrerlo necesita el tiempo t, tendremos AB' = ct. En el mismo tiempo t, A ha pasado a A' con la velocidad v. Tenemos, pues, AA' = vt. Si al rectángulo AA'B' aplicamos el teorema de Pitágoras, tendremos:

$c^{2}t^{2}=l^{2}+v^{2}t^{2}$,

o sea:

$t^{2}(c^{2}-v^{2})=l^{2},\quad t^{2}={\frac {l^{2}}{c^{2}-v^{2}}}={\frac {l^{2}}{c^{2}}}\cdot {\frac {1}{1-\beta ^{2}}},\quad t={\frac {l}{c}}\cdot {\frac {1}{\sqrt {1-\beta ^{2}}}}$.

Para volver, necesita la luz el mismo tiempo, pues la Tierra se desplaza en igual cantidad, llegando el punto de partida A de A' a A''.

Para ir y volver necesita, pues, la luz el tiempo siguiente:

$t_{2}={\frac {2l}{c}}\cdot {\frac {1}{\sqrt {1-\beta ^{2}}}}$

La diferencia entre los tiempos que necesita la luz para recorrer de ida y vuelta una misma distancia, cuando es paralela y cuando es perpendicular al movimiento de la Tierra, es, pues:

$t_{1}-t_{2}={\frac {2l}{c}}\left({\frac {1}{1-\beta ^{2}}}-{\frac {1}{\sqrt {1-\beta ^{2}}}}\right)$

Ahora bien; procediendo como dijimos en la página 138, pueden despreciarse los miembros superiores al segundo orden β y escribir aproximadamente 1 + β², en vez de ${\tfrac {1}{1-\beta ^{2}}}$ y $1+{\tfrac {1}{2}}\beta ^{2}$ en lugar de ${\tfrac {1}{\sqrt {1-\beta ^{2}}}}$ ^[1]. Por lo tanto, puede escribirse con suficiente aproximación:

$t_{1}-t_{2}={\frac {2l}{c}}\left((1+\beta ^{2})-(1+{\tfrac {1}{2}}\beta ^{2})\right)={\frac {2l}{c}}\cdot {\frac {\beta ^{2}}{2}}={\frac {l}{c}}\beta ^{2}$

fig106

El retraso de una de las ondas luminosas con respecto de la otra es, pues, una magnitud del segundo orden. La medición de este retraso puede verificarse por medio del interferómetro de Michelson (fig. 106). En éste (véase pág. 119) la luz que procede de una fuente luminosa Q es dividida en dos rayos por la lámina P semitransparente; esos dos rayos van perpendiculares uno a otro hasta tropezar con los espejos S₁ y S₂; son reflejados por éstos y vuelven otra vez a la lámina P; de aquí entran unidos en la lente de observación F, en donde caen en interferencia. Si las distancias S₁P

y S₂Pson iguales y se coloca uno de los brazos del aparato en la dirección del movimiento de la Tierra, queda realizado exactamente el caso explicado más arriba; los dos rayos llegan, pues, al campo visual con un retraso uno respecto del otro igual a ${\tfrac {l}{c}}\beta ^{2}$. Las rayas de interferencia no están, pues, exactamente donde debieran estar, permaneciendo inmóvil la Tierra. Pero si se hace girar el aparato 90° hasta que el otro brazo esté en dirección paralela al movimiento de la Tierra, tendrán entonces que correrse las rayas de interferencia al otro lado, a igual distancia. Si se observa la posición de las rayas de interferencia durante la rotación misma del aparato, tiene que ser visible un desplazamiento que corresponde al doble retraso.

$2{\frac {l}{c}}\beta ^{2}$

Si T es el periodo de vibración de la luz empleada, la relación entre el retraso y el periodo será ${\tfrac {2l}{cT}}\beta ^{2}$, y como, según la fórmula [31] (pág. 115), la longitud de onda es λ = cT, puede escribirse esa relación así:

$2{\frac {l}{\lambda }}\beta ^{2}$

fig107

Los dos trenes de ondas puestos en interferencia experimentan, al hacer girar el aparato, un desplazamiento, respectivamente uno de otro, cuya relación con la longitud de onda es ${\tfrac {2l\beta ^{2}}{\lambda }}$ (figura 107). Las rayas de interferencia prodúcense, porque los rayos, saliendo del foco luminoso en direcciones algo diferentes, recorren caminos algo diferentes; la distancia de las rayas corresponde a una diferencia entre los caminos igual a una longitud de onda, por lo cual el desplazamiento observable de las rayas es la fracción ${\tfrac {2l\beta ^{2}}{\lambda }}$ de la anchura de franja.

Michelson ha llevado la longitud del recorrido que hace la luz, multiplicando las reflexiones, a 11 m = 1,1 · 10³ cm.; la longitud de onda de la luz empleada era λ = 5,9 · 10^-5 cm. Sabemos que β es aproximadamente igual a 10^-4; esto es β² = 10^-8; de donde se infiere que

${\frac {2l\beta ^{2}}{\lambda }}={\frac {2\cdot 1,1\cdot 10^{3}\cdot 10^{-8}}{5,9\cdot 10^{-5}}}=0,37$

esto es: que las rayas de interferencia deben correrse, al hacer girar el aparato, más de un tercio de su amplitud. Michelson estaba seguro de que aun la centésima parte de tal desplazamiento debería observarse.

Pero cuando se realizó el experimento, no se manifestó el menor rastro del esperado desplazamiento. Posteriores repeticiones con medios aun más refinados no alteraron este resultado. Hay que sacar la conclusión siguiente: No se presenta el viento de éter, y la velocidad de la luz no sufre el influjo del movimiento de la Tierra por el éter, ni aun en las magnitudes del segundo orden.

15. La hipótesis de la contracción.

Michelson mismo concluyó de su experimento que el éter es totalmente arrastrado consigo por la Tierra, al moverse ésta; tal sostenían la teoría elástica de Stokes y la electromagnética de Hertz. Pero a esto se oponen numerosos experimentos que demuestran el arrastre parcial. Michelson inquirió si podría observarse una diferencia de velocidad en la luz a diferentes alturas sobre la superficie de la Tierra; pero no obtuvo resultado positivo; concluyó, pues, que el movimiento del éter arrastrado por la Tierra debe extenderse a muy grandes alturas sobre la superficie de la Tierra. Entonces el éter recibiría el influjo de un cuerpo en movimiento, aun a distancias considerables de este cuerpo; pero éste no es efectivamente el caso, pues Oliver Lodge (1892) demostró que la velocidad de la luz, en las proximidades de cuerpos en movimiento rápido, no recibe de éstos el más mínimo influjo, aun cuando la luz recorra un campo eléctrico o magnético fuerte, arrastrado consigo por el cuerpo.

Pero todos estos esfuerzos parecen casi superfluos, pues aunque hubieren llevado a una explicación aceptable del experimento de Michelson, permanecería, sin embargo, inexplicada la restante electrodinámica y óptica de los cuerpos en movimiento, la cual se pronuncia enteramente en pro de un arrastre parcial.

Un intento de explicación se ofrece al punto al pensamiento, y, en efecto, ha sido desarrollado más tarde sistemáticamente por Ritz (1908). Consiste en la hipótesis de que la velocidad de la luz depende de la velocidad del foco luminoso. Sin embargo, esta hipótesis está bastante en contradicción con todos los resultados teóricos y experimentales de la investigación. En primer término, habría que renunciar al carácter de acción próxima que atribuímos a los procesos electromagnéticos, pues la acción próxima consiste justamente en que la propagación de una acción de sitio en sitio no recibe otra influencia que la de los procesos que se verifican en la inmediata proximidad de cada sitio, y no de la velocidad de un lejano foco luminoso. Por eso Ritz ha caracterizado abiertamente su teoría como una especie de teoría de la emisión; pero lo emitido no serían, naturalmente, partículas materiales obedientes a las leyes mecánicas, sino un agente que, al ingresar en la materia, ejerce sobre los electrones fuerzas dirigidas, transversales, y los impulsa a vibrar. Las vibraciones luminosas existirían, pues, sólo en la materia, no en el éter. La objeción de que en una teoría de la emisión no se explican las interferencias es, evidentemente, inaplicable a esta concepción.

Pero no ha conseguido Ritz llevar su teoría a una perfecta coincidencia con las experiencias ópticas y electromagnéticas; dondequiera que aparecen movimientos relativos del foco luminoso y del observador, manifiéstanse, sin duda, influjos sobre el número de vibraciones (efecto de Doppler) y sobre la dirección (aberración); pero no sobre la velocidad de la luz (experimentos de Arago, página 152, y Hoek, página 153). Ultimamente ha demostrado De Sitter (1913), por medio de una detenida investigación, que la velocidad de la luz procedente de las estrellas fijas es independiente del movimiento de esas estrellas.

Hemos citado esa teoría, a pesar de su fracaso, porque acentúa un pensamiento que es importante para la inteligencia de la teoría de la relatividad; es a saber, el hecho de que todos los procesos observables están siempre adheridos a la materia. El campo en el éter es una ficción, inventada para describir con la mayor posible sencillez las dependencias espaciales y temporales de los procesos en los cuerpos. Habremos de volver más tarde sobre esta concepción.

Ahora nos fijaremos de nuevo en la teoría electrónica de Lorentz, la cual evidentemente veíase puesta en apuradísima situación por el experimento de Michelson. La teoría del éter inmóvil parece exigir indudablemente la existencia del viento de éter en la Tierra y se encuentra, por tanto, en radical oposición al resultado del experimento de Michelson. Si al punto no se deshizo y se vino abajo, es una prueba de su solidez que descansa en la uniformidad e integridad de su imagen física del universo.

Finalmente, logró dominar también esta última dificultad, hasta cierto punto, por medio de una hipótesis muy extraña, que propuso Fitz Gerald (1892) y que Lorentz admitió al punto y elaboró.

Recordemos las reflexiones que constituyen el fundamento del experimento de Michelson. Allí vimos que el tiempo que un rayo necesita para recorrer de ida y vuelta un camino l es diferente, según que este camino sea paralelo o perpendicular al movimiento de la Tierra; y el valor es en el primer caso:

$t_{1}={\frac {2l}{c}}\cdot {\frac {1}{1-\beta ^{2}}}$

y en el segundo caso:

$t_{2}={\frac {2l}{c}}{\frac {1}{\sqrt {1-\beta ^{2}}}}$.

Si admitimos ahora que el brazo del interferómetro, que está en dirección paralela al movimiento de la Tierra, se achica en la proporción de ${\sqrt {1-\beta ^{2}}}:1$; el tiempo t₁ se achicará también en igual proporción, a saber:

$t_{1}={\frac {2l{\sqrt {1-\beta ^{2}}}}{c(1-\beta ^{2})}}={\frac {2l}{c}}\cdot {\frac {1}{\sqrt {1-\beta ^{2}}}}$.

Esto es, que t₁ = t₂.

La hipótesis, sorprendente por su tosquedad y audacia, dice sencillamente: Todo cuerpo que se mueve con respecto al éter con la velocidad v, contráese en la dirección del movimiento en la fracción

${\sqrt {1-\beta ^{2}}}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$.

En realidad, hay que atribuir entonces al experimento de Michelson un resultado negativo, pues para las dos posiciones del interferómetro es t₁ = t₂. Además—y esto es lo esencial—tal contracción no sería determinable, comprobable por ningún medio sobre la Tierra; pues todo instrumento de medida contraeríase igualmente. Un observador que estuviese inmóvil fuera de la Tierra, en el éter, advertiría desde luego la contracción; toda la Tierra estaría para él aplastada en la dirección del movimiento, y todas las cosas sobre ella también.

La hipótesis de la contracción aparece tan extraña y casi absurda porque el acortamiento no se ve obedecer a una fuerza, sino que se presenta como simple circunstancia concomitante del hecho del movimiento. Pero Lorentz no se dejó acobardar por esta objeción; incorporó la hipótesis a su teoría, con tanta mayor decisión cuanto que nuevas experiencias confirmaron que, aun en el segundo orden, no se observa acción alguna del movimiento de la Tierra en el éter.

No podemos aquí ni describir ni discutir en particular todos esos experimentos. Son, en parte, de óptica y se refieren a los procesos de reflexión y refracción, doble refracción, rotación del plano de polarización, etc.; en parte son electromagnéticos, y se refieren a los fenómenos de inducción, distribución de la corriente en hilos, etc. La técnica física permite hoy determinar si en esos procesos existe o no un influjo del segundo orden producido por el movimiento de la Tierra. Particularmente digno de atención es un experimento de Trouton y Noble (1903) para hallar una fuerza de rotación que debiera, a consecuencia del viento de éter, presentarse en un condensador de placas colgado.

Todos estos experimentos dieron, sin excepción, resultados negativos. No podía seguirse dudando: un movimiento de traslación por el éter no puede ser percibido por el observador que lo realiza. El principio de relatividad, válido en la mecánica, extiende, pues, su validez a la totalidad de los procesos electromagnéticos.

Lorentz se proponía conciliar tal hecho con su teoría del éter; y no parecía que hubiese otro camino que el de admitir la hipótesis de la contracción y elaborarla con las leyes de la teoría electrónica para constituir un conjunto unitario y coherente. Ante todo, advirtió que un sistema de cargas eléctricas que se mantienen en equilibrio por sólo la acción de sus fuerzas electrostáticas, se contrae por sí mismo tan pronto como es puesto en movimiento; o, dicho más exactamente, las fuerzas electromagnéticas que se presentan al moverse el sistema con movimiento uniforme alteran la configuración del equilibrio; de suerte que toda longitud es acortada en la dirección del movimiento en el factor ${\sqrt {1-\beta ^{2}}}$.

Esta ley matemática conduce a una explicación de la contracción, si se admite que todas las fuerzas físicas son en el fondo de origen eléctrico o, por lo menos, que obedecen a las mismas leyes del equilibrio en sistemas movidos uniformemente. La dificultad de considerar todas las fuerzas como eléctricas proviene de que éstas, según antiguas leyes, que proceden de Gauss, conducen sin duda a equilibrios, mas nunca a equilibrios estables de cargas. Las fuerzas que juntan los átomos en moléculas y éstas en cuerpos sólidos no pueden ser, pues, simplemente eléctricas. La necesidad de admitir fuerzas no eléctricas aparece clarísima cuando se pregunta por la constitución dinámica del electrón mismo. Este es un montón de carga negativa; hay que atribuir a ésta una extensión finita, pues, como ya hemos visto (pág. 230), la energía de una carga de forma esférica con radio a es igual a ${\tfrac {1}{2}}{\tfrac {e^{2}}{a}}$ y se hace infinitamente grande cuando se pone a = 0. Las partes singulares del electrón tienden, empero, a separarse, pues las cargas del mismo signo se repelen. Por consiguiente, debe haber una fuerza extraña que las mantenga unidas. En la teoría del electrón, expuesta por Abraham, se admite que es éste una esfera rígida, es decir, que las fuerzas no eléctricas son tan grandes que no permiten deformación alguna. Pero cabe, naturalmente, hacer otras hipótesis.

Para Lorentz presentábase la hipótesis de que también el electrón sufre la contracción ${\sqrt {1-\beta ^{2}}}$; ya hemos dicho antes (página 235) que se obtiene así una fórmula mucho más sencilla que la de Abraham para la masa del electrón. El electrón de Lorentz tiene, empero, además de la energía electromagnética, una energía de deformación, cuyo origen es extraño, la cual falta en el electrón rígido de Abraham.

Lorentz investigó la cuestión de si la hipótesis de la contracción basta para deducir la relatividad. En cálculos difíciles estableció que no es el caso así; pero halló también (1899) la hipótesis que debe añadirse para que todos los procesos electromagnéticos en sistemas en movimiento transcurran exactamente como en el éter. Su resultado es, por lo menos, tan extraño como la hipótesis de la contracción; dice así: en un sistema movido con movimiento uniforme hay que emplear otra medida del tiempo. A esta medida del tiempo, que varía de sistema en sistema, llamóla tiempo local. La hipótesis de la contracción puede expresarse diciendo que la unidad de medida en los sistemas en movimiento es distinta que en el éter. Las dos hipótesis juntas dicen, pues, que el espacio y el tiempo deben medirse, en sistemas movidos, de distinta manera que en el éter. Lorentz indicó las leyes que sirven para transformar las medidas en diferentes sistemas movidos unos con respecto de otros, y demostró que en tales transformaciones permanecen invariadas las ecuaciones de los campos de la teoría electrónica. Tal es el alcance matemático de su descubrimiento. Estas conexiones las estudiaremos en seguida, desde el punto de vista de Einstein, en forma mucho más clara, y por eso no insistimos ahora sobre ellas. Pero vamos a ver ahora qué consecuencias tiene la nueva concepción de la teoría de Lorentz para la representación del éter.

En la nueva teoría de Lorentz, el principio de relatividad rige, en concordancia con la experiencia, para todos los procesos electrodinámicos; un observador percibe en su sistema los mismos procesos, ya sea que el sistema esté inmóvil en el éter, o se halle en movimiento rectilíneo uniforme. No posee, pues, medio alguno para distinguir uno de otro, pues aun la observación de otros cuerpos en el mundo, que se muevan independientemente de él, no le enseña mas que su movimiento relativo con respecto a esos cuerpos, pero nunca el movimiento absoluto con respecto del éter. Puede, pues, afirmar que está inmóvil en el éter, sin que nadie pueda refutarle. Desde luego, otro observador en otro cuerpo que se mueve respecto del primero, puede afirmar otro tanto con igual derecho. No hay ningún medio empírico ni teórico para decidir si uno de los dos, y cuál de los dos, tiene razón.

Llegamos aquí, pues, con respecto del éter, a la misma situación en que el principio clásico de la relatividad en la mecánica nos puso con respecto del espacio absoluto de Newton (III, 6, pág. 85). Allí hubimos de confesar que es absurdo reconocer un determinado lugar en el espacio absoluto como algo real en el sentido de la física; pues no existe ningún medio mecánico para fijar un lugar o volverlo a encontrar en el espacio absoluto. De igual modo hay que confesar ahora que un determinado lugar en el éter no es nada real físicamente hablando, con lo cual el éter mismo pierde por completo el carácter de substancia. Es más; puede decirse incluso: si de dos observadores que se mueven uno con respecto del otro puede decir cada uno con igual derecho que se halla inmóvil en el éter, es que no hay éter.

La teoría del éter llega, pues, en su evolución suprema, a suprimir su concepto fundamental. Pero ha costado mucho trabajo decidirse a reconocer la vacuidad de la representación del éter; el mismo Lorentz, cuyos profundos pensamientos, cuya incansable labor ha conducido la teoría del éter a la crisis que reseñamos, el mismo Lorentz ha vacilado mucho tiempo antes de dar el paso decisivo. Y el motivo es que el éter ha sido expresamente pensado e inventado para servir de sustentáculo a las vibraciones luminosas, o más generalmente a las fuerzas electromagnéticas en el espacio vacío. En realidad, no cabe pensar oscilaciones sin algo que oscile. Pero ya antes, al reseñar la teoría de Ritz, hemos advertido que la afirmación de que también en el espacio vacío existen determinables vibraciones excede y rebasa toda experiencia posible. La luz o las fuerzas electromagnéticas no son determinables sino en la materia; el espacio vacío y libre de toda materia no es objeto de observación. Sólo es posible determinar lo siguiente: de tal cuerpo material sale una acción que alcanza a aquel otro cuerpo material algún tiempo después. Lo que ocurre entremedias es puramente hipotético o, dicho con más energía, caprichoso; esto significa que la teoría puede atribuir al vacio magnitudes de estado, campos o lo que sea, a su capricho, con la única condición que las variaciones observadas en los cuerpos materiales queden reducidas a una conexión firme y clara.

Esta concepción es un paso más en el sentido de la mayor abstracción, de la liberación de acostumbradas intuiciones, que son, al parecer, necesarios elementos del mundo de las representaciones. Y al mismo tiempo acércase al ideal de la física, que consiste en no admitir como pilares del universo físico nada más que lo que la experiencia ofrece directamente, proscribiendo todas las imágenes innecesarias y todas las analogías que proceden de un estado primitivo y grosero de la experiencia.

El éter substancial desaparece desde ahora de la teoría. En su lugar pónese el «campo electromagnético» abstracto, como simple auxiliar matemático, útil para describir cómodamente los procesos en la materia y sus conexiones regulares ^[2].

El que se atemorice ante tal concepción formal, que piense en la abstracción siguiente, que es muy análoga y a la cual hace tiempo que está acostumbrado:

Para determinar el lugar en la superficie terrestre, sitúanse en las torres, en las montañas y otros puntos visibles signos trigonométricos, en los cuales se señala la longitud y la latitud geográfica. Pero en el mar nada de eso existe; las longitudes y latitudes son solamente pensadas o, como se dice también, virtuales. Cuando un barco quiere determinar un lugar, entonces, por medio de observaciones astronómicas, transforma en una realidad lo que es una mera intersección de esas lineas imaginarias, hace del lugar virtual un lugar real. Del mismo modo debe concebirse el campo electromagnético. La tierra firme corresponde a la materia; las señales trigonométricas, a las variaciones físicas determinables. El mar, empero, corresponde al vacío, y los círculos meridianos y paralelos, al campo electromagnético imaginado. Este es virtual, hasta que un cuerpo de ensayo se le acerca y lo hace visible por medio de sus reales variaciones; justamente como el barco realiza el lugar goegráfico virtual.

Sólo quien se haya apropiado realmente esta manera de concebir, logrará entender la posterior evolución de la doctrina del espacio y el tiempo. Los diferentes hombres son diferentemente accesibles a la progresiva abstracción, objetivación y relativización. Los antiguos pueblos cultos del continente europeo, alemanes, holandeses, escandinavos, franceses e italianos la conciben con mayor facilidad, y son los que más vivamente participan en la elaboración del sistema. Los ingleses, inclinados a las representaciones concretas, son ya más difícilmente accesibles. El americano gusta de atenerse a imágenes y modelos mecánicos; el mismo Michelson, cuyos trabajos experimentales han tenido principalísima parte en la destrucción de la teoría del éter, rechaza una teoría de la luz sin éter, como algo impensable. Pero la reciente generación, educada por doquiera en el sentido de las nuevas concepciones, admite como evidencias lo que para las generaciones pretéritas eran novedades inauditas.

Si resumimos la evolución, vemos que la teoría del éter ciérrase con el principio de relatividad y halla su fin en éste. El éter substancial desaparece como hipótesis innecesaria, y el principio de relatividad preséntase claramente como ley fundamental de la física. Plantéase, pues, el problema de reconstruir el edificio del mundo físico sobre esa base segura. Llegamos así, por fin, a los trabajos de Einstein.

1. Pues si x es un número pequeño, cuyo cuadrado puede ser despreciado, tenemos:
   $(1+x)(1-x)=1-x^{2}$, aproximadamente = 1

   y, por lo tanto:

   $1+x={\frac {1}{1-x}}$,
   o sea:
   ${\begin{aligned}(1-x)(1+{\tfrac {1}{2}}x)^{2}&=(1-x)(1+x+{\tfrac {1}{4}}x^{2})\\{\text{aproximadamente}}&=(1-x)(1+x)=1-x^{2}\\{\text{aproximadamente}}&=1,\end{aligned}}$

   y, por lo tanto:

   ${\begin{aligned}(1+{\tfrac {1}{2}}x)^{2}&={\frac {1}{1-x}},\\1+{\tfrac {1}{2}}x&={\frac {1}{\sqrt {1-x}}}.\end{aligned}}$

   Si en las dos fórmulas aproximadas se pone β² en lugar de x, se obtienen las aproximaciones empleadas en el texto, a saber:

   ${\frac {1}{1-\beta ^{2}}}=1+\beta ^{2},\quad {\frac {1}{\sqrt {1-\beta ^{2}}}}=1+{\tfrac {1}{2}}\beta ^{2}$.
2. Einstein ha propuesto recientemente que llamemos éter al espacio vacío provisto de campos gravitatorios y electromagnéticos; esta palabra no deberá designar ninguna substancia con los atributos tradicionales; así, en ese éter no hay puntos determinables, y es absurdo hablar de un movimiento con relación al éter. El uso que propone Einstein de la palabra éter es admisible naturalmente, y si se hace habitual, será bastante cómodo.