La teoría de la relatividad de Einstein/VI

VI

EL PRINCIPIO ESPECIAL DE LA RELATIVIDAD DE EINSTEIN

1. El concepto de la simultaneidad.

Las dificultades lógicas que era preciso dominar al desenvolver el principio de relatividad en los procesos electrodinámicos, obedecen a que es necesario conciliar las dos proposiciones siguientes:

1.ª Según la mecánica clásica, la velocidad de cualquier movimiento tiene diferentes valores para dos observadores en movimiento relativo uno a otro.

2.ª Pero la experiencia enseña que la velocidad de la luz tiene siempre el mismo valor c, independientemente del estado de movimiento en que se halle el observador.

La vieja teoría del éter intentó disipar la contradicción de las dos proposiciones anteriores, dividiendo la velocidad de la luz en dos sumandos, la velocidad del éter lumínico y la velocidad de la luz con respecto al éter, con lo cual la primera participación podía ser determinada apropiadamente merced a hipótesis de arrastre. Pero de esta suerte sólo se consigue disipar la contradicción por lo que se refiere a magnitudes del primer orden. La teoría de Lorentz, para mantener en vigor la ley de la constancia de la velocidad de la luz, hubo de introducir para cada sistema en movimiento una especial medida de longitud y de tiempo; prodúcese entonces la constancia de la velocidad de la luz por una especie de «engaño físico».

Einstein reconoció (1905) que en la contracción y en el tiempo local de Lorentz no se trata de un artificio matemático, ni tampoco de ilusión o engaño físico, sino de los fundamentos de los conceptos de espacio y tiempo en general.

De las dos proposiciones 1 y 2, es la primera puramente teórica y conceptual, mientras que la segunda está fundada empíricamente.

Ahora bien; como la segunda, la ley de la constancia de la velocidad de la luz, tiene que valer con certeza completa experimental, no queda más recurso que negar la primera, y con ella los principios de la determinación del espacio y del tiempo, tal como hasta ahora han sido empleados. Tiene, pues, que haber en estos principios un error o, por lo menos, un prejuicio, una confusión entre hábitos y necesidades del pensamiento, obstáculo conocido a todo progreso.

Y el prejuicio reside en el concepto de simultaneidad.

Pasa por evidente que tiene buen sentido la proposición siguiente: un suceso que ocurre en el lugar A, por ejemplo, en la Tierra, y otro suceso que ocurre en el lugar B, por ejemplo, en el Sol, son simultáneos. Al decir esto, se supone que conceptos tales como momento del tiempo, simultaneidad, antes, después, etc., poseen en sí mismos, a priori, una significación válida para el conjunto del universo. En este punto de vista colocóse Newton cuando postuló la existencia de un tiempo absoluto o duración absoluta (III, 1, pág. 67) que transcurre «uniformemente y sin referencia a ningún objeto exterior».

Mas para el físico, que verifica mediciones, no existe tal tiempo. Para él la afirmación de que un suceso en A y otro suceso en B son simultáneos, no tiene en absoluto un sentido; pues no posee ningún medio para decidir si la afirmación es exacta o falsa.

En efecto; para poder juzgar la simultaneidad de dos sucesos que se verifican en distintos lugares, hay que colocar en cada uno de esos lugares relojes de los cuales se tenga la seguridad de que andan iguales, «sincrónicos». La cuestión viene, pues, a parar a esta otra: ¿puede indicarse un medio de comprobar la marcha igual de dos relojes colocados en dos lugares diferentes?

Imaginemos los dos relojes inmóviles en un sistema de referencia S, situados en A y en B, a una distancia l uno de otro. Puede regularse la marcha de los dos relojes de dos maneras:

1.ª Se ponen los dos en el mismo sitio; se regulan hasta que anden exactamente iguales, y se llevan luego cada uno a su sitio en A y en B.

2.ª Se utilizan señales luminosas para comparar los relojes.

Ambos métodos se usan en la práctica. Un navío lleva un cronómetro que ande muy bien y que esté regulado por el reloj normal de su puerto de origen; pero además recibe señales por telegrafía sin hilos.

El hecho de que se consideren necesarias estas señales demuestra la desconfianza que inspira el reloj del barco. La inferioridad práctica del método que consiste en emplear relojes transportables obedece a que el más pequeño error se multiplica continuamente durante la marcha. Pero aun cuando se admita que existen relojes ideales, sin errores—como los que el físico está convencido que posee cuando usa como reloj las vibraciones atómicas al enviar luz—, sin embargo, es inadmisible lógicamente establecer la definición del tiempo sobre ellos, en sistemas que se muevan relativamente uno a otro. Pues la marcha igual de dos relojes, por buenos que sean, podrá comprobarse directamente, es decir, sin el empleo de señales, sólo en el caso de que estén los dos inmóviles uno con respecto al otro. Pero si están en movimiento relativo uno a otro, no podrá comprobarse sin señales la marcha igual; seria una pura hipótesis que, según los principios de la investigación física, debemos tratar de evitar. Por lo cual nos vemos obligados a preferir el método de las señales para definir el tiempo en sistemas que se muevan relativamente uno a otro; si llegamos así a un método coherente de medición del tiempo, habremos luego de investigar cómo debe estar constituido un reloj ideal, para indicar siempre el tiempo «exacto» en cualesquiera sistemas en movimiento (VI, 5, pág. 275).

Imaginemos un tren de remolque en el mar, consistente en un remolcador A y algunos barcos de carga B, C, D. El viento está en calma, y hay tanta niebla, que un barco no es visible desde el otro. Trátase ahora de comparar los relojes en los barcos; habrá que emplear señales acústicas. El remolcador A, a las 12, disparará un cañonazo, y cuando la detonación se perciba en los barcos, pondrán éstos sus relojes en las 12. Pero al operar así, cométese evidentemente un pequeño error, pues el sonido necesita un cierto tiempo para ir de A a B, C. Si es conocida la velocidad c del sonido, puede corregirse ese error. La velocidad c del sonido es aproximadamente 340 m./sec. Si el barco B va detrás de A a una distancia l = 170 m., necesitará el sonido $t={\tfrac {l}{c}}={\tfrac {170}{340}}={\tfrac {1}{2}}$ segundo para ir de A a B, y, por tanto, el reloj de B deberá ponerse en las 12 y ½ segundo, cuando se oiga la detonación. Pero la corrección ésta no es exacta, sino en el caso de que el tren de remolque esté inmóvil; pues si está en movimiento, necesitará evidentemente el sonido menos tiempo para ir de A a B, puesto que el barco B va al encuentro de la onda sonora. Si se quiere hacer la corrección exacta, hay que conocer la velocidad absoluta del barco con respecto al aire. Si ésta es desconocida, es imposible verificar una absoluta comparación del tiempo por medio del sonido. Si el tiempo es claro, pueden usarse señales luminosas en lugar de disparos; como la luz es extraordinariamente más rápida, el error será pequeñísimo; pero en una consideración de principios no importan las cantidades absolutas. Imaginemos, en lugar del tren de remolque en el mar, un astro en el mar de éter, y en lugar de la señal acústica, una señal luminosa; todas las reflexiones que hemos hecho permanecerán intactas. En el espacio cósmico no hay mensajero más rápido que la luz. Vemos, pues, que la teoría del éter absolutamente inmóvil lleva a la conclusión siguiente: no es posible realizar una comparación absoluta del tiempo, en sistemas en movimiento, si no se conoce el movimiento del sistema con respecto del éter.

Pero el resultado de todas las investigaciones experimentales ha sido que un movimiento con respecto al éter no es comprobable por ninguna observación física. De aquí se infiere que una simultaneidad absoluta no puede tampoco comprobarse nunca de ninguna manera.

Desaparece lo paradójico de esta afirmación cuando se ve claramente que para comparar el tiempo por medio de señales luminosas hay que conocer de antemano el valor exacto de la velocidad de la luz; pero para medir esta velocidad hace falta saber de antemano determinar una duración del tiempo. Hay aquí evidentemente un circulo vicioso.

Pero si no es posible llegar a una simultaneidad absoluta, cabe, sin embargo, como observa Einstein, definir una simultaneidad relativa para todos los relojes que se encuentren unos con respecto a otros en relativa inmovilidad, y para ello no hace falta conocer el valor de la velocidad de las señales.

fig108

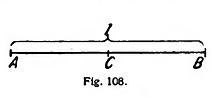
Vamos a demostrarlo primero sobre el ejemplo de nuestro tren de remolque. Hallándose éste en reposo, podrá conseguirse una marcha igual de los relojes situados en los barcos A y B, del modo siguiente (fig. 108): se colocará un bote C exactamente en el centro de la amarra entre A y B, y se disparará un tiro en el bote. El tiro se oirá simultáneamente en A y en B.

Pero si el tren de remolque S está en movimiento, cabe, naturalmente, emplear el mismo procedimiento; y si los marineros no caen en la cuenta de que están en movimiento con respecto al aire, quedarán convencidos de que los relojes en A y B andan iguales.

Otro tren de remolque S', cuyos barcos A', B', C' están separados por las mismas distancias exactamente que los correspondientes del primer tren S ha regulado sus relojes de la misma manera. Supongamos ahora que uno de los trenes alcanza al otro, ya sea que éste esté inmóvil, o que ande también; habrá un momento en que el barco A pasará junto a A' y el barco B junto a B', y los marineros podrán comprobar si sus relojes concuerdan. Naturalmente hallarán que no; si, por acaso, A y A' son sincrónicos, no lo serán B y B'.

Y así se manifestará el error; en marcha, necesita evidentemente la señal que parte del centro C más tiempo para llegar al barco delantero A que al barco trasero B, porque A se va alejando de la onda sonora, mientras que B va al encuentro de ella; y esta diferencia es distinta si las velocidades de los dos trenes de remolque son distintas.

En el caso de las señales acústicas habrá un sistema que tenga el tiempo exacto, el que esté inmóvil con respecto al aire. Pero en el caso de señales luminosas no hay posibilidad de afirmarlo, porque el movimiento absoluto con respecto al éter luminoso es un concepto que, según todas las experiencias, carece de realidad física. El método para regular los relojes que hemos reseñado sobre el ejemplo del sonido es, naturalmente, posible también empleando la luz: los relojes de A y B pueden ponerse de tal manera que toda señal luminosa procedente del centro C de la distancia A B llegue a esos relojes cuando éstos muestren idéntica posición de sus manecillas. De esta suerte puede establecer un sistema cualquiera S el sincronismo de sus relojes; pero cuando dos de estos sistemas en movimiento uniforme rectilíneo uno con respecto del otro se encuentren, si por caso coinciden los relojes A y A', no coincidirán los relojes B y B', que marcarán diferente posición de sus manecillas. Ambos sistemas pueden, con igual derecho, pretender la posesión del tiempo exacto; pues cualquiera de los dos puede afirmar que está en reposo, ya que todos las leyes naturales son iguales en ambos.

Pero si dos ostentan con igual derecho una misma pretensión, que, según el sentido de ésta, sólo a uno podría corresponder, hay que concluir entonces que la pretensión no tiene sentido.

No hay simultaneidad absoluta.

Quien haya entendido esto bien, no comprenderá fácilmente que hayan transcurrido tantos años de investigación exacta antes de reconocer este sencillo hecho. Es la eterna historia del huevo de Colón.

El problema que se plantea inmediatamente es el siguiente: el método de comparar relojes que hemos empleado ¿conduce a un concepto relativo del tiempo que esté libre de contradicción?

Efectivamente, así es. Para comprenderlo, vamos a emplear la exposición de Minkowski, que consiste en representar los sucesos o puntos universales en un plano xt. Nos limitaremos a los movimientos en la dirección x y prescindiremos, por tanto, de y y z (fig. 109).

fig109

Los puntos A, B, C, inmóviles en el eje x, son representados, en el sistema S de las coordenadas xt, como tres paralelas al eje t. El punto C hállase en el centro de AB. Una señal luminosa parte de él, en el tiempo t = 0, dirigiéndose en ambas direcciones.

Admitimos que el sistema S está «quieto», es decir, que la velocidad de la luz es idéntica en ambas direcciones; las señales luminosas que van hacia la derecha y la izquierda son entonces representadas por rectas oblicuas al eje x y que llamamos «líneas luminosas». Admitiremos que la inclinación sea de 45°, lo cual, evidentemente, se deriva de que la distancia que en la figura representa la unidad de longitud, 1 cm. sobre el eje x, significa sobre el eje t el brevísimo tiempo ${\tfrac {1}{c}}$ sec., que la luz necesita para recorrer 1 cm. de camino.

Las intersecciones A₁B₁ de las líneas luminosas con las líneas universales de los puntos A y B darán, por sus valores t, los momentos de llegar las dos señales luminosas. Se ve que A₁ y B₁ están sobre una paralela al eje x; esto es, son simultáneos.

Supongamos ahora que los tres puntos A, B y C se mueven uniformemente con igual velocidad; sus líneas universales serán nuevamente paralelas, pero oblicuas sobre el eje x (fig. 110). Las señales luminosas son representadas por las mismas líneas anteriores que parten de C; pero sus intersecciones A₁' y B₁' con las líneas universales A y B no están ahora situadas en una paralela al eje x; no son, pues, simultáneas en el sistema de coordenadas xt, sino que B₁' es posterior a A₁'. En cambio, un observador que se mueva con el sistema, afirmará con igual derecho que A₁'B₁' son sucesos (puntos universales) simultáneos; este observador usará un sistema S' de coordenadas x't', en el cual los puntos A₁' y B₁' estarán en una paralela al eje x. Las líneas universales de los puntos A, B y C son, naturalmente, paralelas al eje t' por A, B y C en el sistema S' están inmóviles, y sus coordenadas x' tienen el mismo valor para todos los t'.

fig110

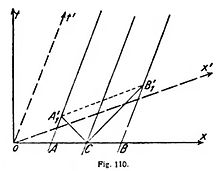
De aquí se deriva que el sistema en movimiento S' en el plano xt es representado por un sistema de coordenadas a ángulo agudo x't', en el cual los dos ejes están inclinados con respecto a los primitivos.

Recordaremos que en la mecánica corriente los sistemas inerciales eran representados en el plano xt también por coordenadas acutangulares con eje t dirigido de cualquiera manera, quedando empero el eje x siempre idéntico (III, 7, pág. 86). Ya allí hubimos de advertir que esto es, desde un punto de vista matemático, un defecto de belleza que la teoría de la relatividad suprime. Ahora se ve claramente cómo ello se realiza merced a la nueva definición de la simultaneidad. Al mismo tiempo, con sólo mirar la figura, sin necesidad de cálculos se llega a la convicción de que esa definición, perfectamente coherente en sí misma, es posible; pues no significa otra cosa que el empleo de coordenadas acutangulares, en vez de coordenadas rectangulares.

Las unidades de la longitud y del tiempo en el sistema acutangular no están aún determinadas por la construcción; en esta se hace uso del hecho de que la luz se propaga con igual rapidez en todas las direcciones en un sistema S; pero todavía no se emplea la ley de que la velocidad de la luz tiene el mismo valor c en todos los sistemas inerciales. Si se tiene en cuenta este último hecho, se llega a la mecánica completa de Einstein.

2. La cinemática de Einstein y las transformaciones de Lorentz.

Repetiremos una vez más los supuestos en que se basa la cinemática de Einstein:

1.° Principio de relatividad.—Hay infinitos sistemas de referencia en movimiento relativo uniforme y rectilíneo (sistemas de inercia), en los cuales todas las leyes naturales adoptan la figura más sencilla (originariamente derivada en el espacio absoluto o el éter inmóvil).

2.° Principio de la constancia de la velocidad de la luz.— En todos los sistemas inerciales la velocidad de la luz, medida con metros y relojes físicamente homogéneos, tiene el mismo valor.

El problema es derivar de aquí las relaciones entre longitudes y tiempos en los distintos sistemas inerciales. Nos limitaremos a movimientos que sean paralelos a una dirección fija del espacio, la dirección x.

Consideremos dos sistemas inerciales S y S' que tengan la velocidad relativa v. El punto cero del sistema S' tendrá, pues, con respecto del sistema S, en el tiempo t, la coordenada x = vt; su línea universal hállase caracterizada en el sistema S' por la condición x' = 0. Las dos ecuaciones deben significar lo mismo, por lo cual x - vt debe ser proporcional a x': establecemos

$\alpha x'=x-vt$.

Según el principio de relatividad son, empero, igualmente legítimos ambos sistemas; pues puede aplicarse la misma consideración al movimiento del punto cero de S, relativamente a S', teniendo en cuenta tan sólo que la velocidad relativa v tenga el signo contrarío. Por lo tonto, x'—t' debe ser proporcional a x, y como los dos sistemas son de igual valor, tendrá el mismo factor de proporcionalidad α:

$\alpha x=x'+vt'$.

De esta ecuación, y merced a la primera, puede expresarse t' por x y t; se halla

$vt'=\alpha x-x'=\alpha x-{\frac {x-vt}{\alpha }}={\frac {1}{\alpha }}\left[(\alpha ^{2}-1)+vt\right]$

y, por tanto:

$\alpha t'={\frac {\alpha ^{2}-1}{v}}x+t$.

Esta ecuación, unida a la primera, permite calcular x' y t' cuando se conocen x y t. Queda, sin embargo, indeterminado el factor de proporcionalidad α; hay que elegirlo de modo que se mantenga el principio de la constancia de la velocidad de la luz.

La velocidad de un movimiento uniforme represento en el sistema S por $u={\tfrac {x}{t}}$, y en el sistema S' por $u'={\tfrac {x'}{t'}}$. Si se dividen las dos ecuaciones que nos permiten expresar x' y t' por x y t, elimínase el factor α y se obtiene:

$u'={\frac {x'}{t'}}={\frac {x-vt}{{\frac {\alpha ^{2}-1}{v}}x+t}}$;

si dividimos el numerador y el denominador de la derecha por t y ponemos u = ${\tfrac {x}{t}}$, obtendremos:

$u'={\frac {u-v}{{\frac {\alpha ^{2}-1}{v}}u+1}}$[63]

Si se trata particularmente del movimiento uniforme de un rayo luminoso a lo largo del eje x, tendrá que ser u = u' según el principio de la constancia de la velocidad de la luz; su valor común es justamente la velocidad de la luz c. Si ponemos, por consiguiente, en nuestra fórmula u = c y al mismo tiempo u' = c, tendremos:

$c={\frac {c-v}{{\frac {\alpha ^{2}-1}{v}}c+1}},\quad {\text{o sea}}\quad {\frac {\alpha ^{2}-1}{v}}c^{2}+c=c-v$;

de aquí se sigue:

$\alpha ^{2}-1=-{\frac {v^{2}}{c^{2}}}=-\beta ^{2}$,

o sea:

$\alpha ^{2}+\beta ^{2}=1$

Queda así descubierto el factor de proporcionalidad α, a saber:

$\alpha ={\sqrt {1-\beta ^{2}}}$[64]

Las fórmulas de transformación son, pues:

$\alpha x=x-vt,\quad \alpha t'=-{\frac {\beta ^{2}}{v}}x+t$.

Las escribiremos una vez más extensamente, y añadiremos las coordenadas yz perpendiculares a la dirección del movimiento y que no varían:

$x'={\frac {x-vt}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad y'=y,\quad z'=z,\quad t'={\frac {t-{\frac {v}{c^{2}}}x}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$[65]

Estas reglas por las cuales pueden calcularse el lugar y el tiempo de un punto universal en el sistema S', cuando son dadas en el sistema S, llevan el nombre de transformación de Lorentz. Son, efectivamente, las mismas fórmulas que halló Lorentz por difíciles reflexiones sobre la invariancia de las ecuaciones de Maxwell.

Si se quiere expresar x, y, z, t por medio de x', y', z', t' hay que resolver las ecuaciones; puede inferirse sin cálculo, por la equivalencia de ambos sistemas S y S' que las fórmulas de resolución tendrán la misma forma, con sólo poner -v en lugar de v. Y el cálculo, efectivamente, da:

$x={\frac {x'+vt'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad y=y',\quad z=z',\quad t={\frac {t'+{\frac {v}{c^{2}}}x'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$.

Tiene especial interés el caso limite, en donde la velocidad v de ambos sistemas sea muy pequeña con relación a la velocidad de la luz c; en este caso se llega a la transformación de Galileo [fórmula 25] (pág. 90). Pues si ${\tfrac {v}{c}}$ puede despreciarse, se obtendrá por la fórmula [65]:

$x'=x-vt,\quad y'=y,\quad z'=z,\quad t'=t$.

Se comprende, pues, que siendo tan pequeño el valor de ${\tfrac {v}{c}}$ en todos los casos prácticos, la cinemática de Galileo satisfará por muchos siglos a todas las necesidades.

3. Exposición geométrica de la cinemática de Einstein.

Antes de intentar la interpretación del contenido de estas fórmulas, vamos a exponer geométricamente las relaciones que ellas expresan entre dos sistemas inerciales, siguiendo el método introducido por Minkowski, esto es, el de tomar un sistema de coordenadas cuatridimensional, el universo xyzt. Podemos prescindir de las coordenadas y y z, que permanecen invariables, y limitarnos a considerar el plano xt. Todas las leyes cinemáticas aparecen entonces como hechos geométricos en el plano xt. Pero debemos aconsejar al lector que las relaciones adquiridas en forma geométrica las vaya traduciendo continuamente en el lenguaje usual de la cinemática. Deberá, pues, el lector entender por línea universal el movimiento de un punto, y por intersección de dos líneas universales el encuentro de dos puntos en movimiento, y así sucesivamente. Puede facilitarse mucho la imaginación de los procesos representados en las figuras, tomando una regla colocándola paralelamente al eje x, moviéndola en la dirección del eje t y considerando las intersecciones del borde de la regla con las líneas universales; estos puntos se mueven entonces de acá para allá al borde de la regla y dan una imagen del curso espacial del movimiento.

Cada sistema inercial S queda expuesto por una cruz de ángulos agudos en el plano xt, como ya hemos visto (VI, 1, página 251); que alguna de esas cruces sea rectangular es cosa que deberá considerarse como contingente y no juega papel alguno.

Cada punto del espacio puede ser punto de partida de una onda luminosa que se extiende en todas las direcciones uniformemente, como una esfera. A lo largo de la única dirección que aquí consideramos, la dirección x, existen de esa onda esférica sólo dos señales luminosas, una de las cuales va hacia la izquierda y la otra hacia la derecha. Serán, pues, representadas en el plano xt por dos rectas en cruz, que son, naturalmente, independientes de la elección del sistema de referencia, puesto que enlazan entre sí sucesos reales, puntos universales; esto es, los lugares del espacio que la señal luminosa va encontrando uno tras otro.

Dibujamos esas líneas luminosas para un punto universal, que será al mismo tiempo el punto cero de todos los sistemas de coordenadas xt considerados; y las dibujaremos como dos rectas perpendiculares, y éstas las elegimos como ejes de un sistema de coordenadas ξη. (fig. 111).

Tenemos así a la vista una de las dos características de la teoría de Einstein: el sistema ξη está determinado unívocamente y firme en el «mundo», aunque sus ejes no son rectas espaciales, sino formadas por los puntos universales que alcanza una señal luminosa partiendo del punto cero. Este sistema de coordenadas invariantes o absolutas es, pues, de naturaleza sumamente abstracta. Hay que acostumbrarse a que tales abstracciones substituyan en la teoría moderna a la representación concreta del éter; su fuerza está en que no contienen nada que exceda de los conceptos necesarios para interpretar la experiencia.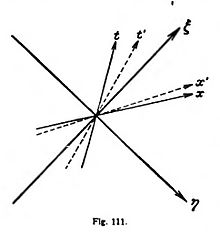

fig111

A este sistema absoluto de referencia ξη, han de estar estrechamente unidas las curvas estimativas que seccionan las unidades de longitud y tiempo en los ejes de cualquier sistema inercial xt. Esas curvas deben quedar expuestas por una ley invariante, y se trata de encontrarla.

Las líneas luminosas son invariantes. El eje ξ (η = 0) queda expuesto en un sistema de referencia S por la fórmula x = ct, y en otro sistema de referencia S' por la fórmula x' = ct'; pues éstas expresan que la velocidad de la luz en ambos sistemas tiene el mismo valor. Vamos ahora a calcular, por la transformación de Lorentz [65], y con las coordenadas x, t, la diferencia x' - ct' que para los puntos del eje η, es igual a cero; se sigue que

${\begin{aligned}x'-ct'&={\frac {1}{\alpha }}\left[(x-vt)-c\left(t-{\frac {v}{c^{2}}}x\right)\right]\\&={\frac {1}{\alpha }}\left[x\left(1+{\frac {v}{c}}\right)-ct\left(1+{\frac {v}{c}}\right)\right]\\&={\frac {1+\beta }{\alpha }}(x+ct).\end{aligned}}$

Por donde se ve que, siendo x - ct = 0, será también x' - ct' = 0.

Para el eje η (ξ = 0) es x = -ct y x' = -ct'; si hacemos el correspondiente cálculo de x' + ct' con x, t, nos bastará, en la fórmula anterior, poner -c en lugar de c, y -β en lugar de β (mientras que $\alpha ={\sqrt {1-\beta ^{2}}}$ permanece inalterado), y tendremos:

$x'+ct'={\frac {1-\beta }{\alpha }}(x+ct).$

Pero de estas dos fórmulas se infiere fácilmente una formación invariante; en efecto,

$(1+\beta )(1-\beta )=1-\beta ^{2}=\alpha ^{2},$

de donde, multiplicando las dos ecuaciones una por otra, recibirá el factor el valor 1 y se hallará:

$(x'-ct')(x'+ct')=x^{2}-c^{2}t^{2}$

o sea:

$x'^{2}-c^{2}t'^{2}=x^{2}-c^{2}t^{2};$

por donde tenemos que la expresión

$G=x^{2}-c^{2}t^{2}$[66]

es invariante. A causa de su carácter fundamental, la llamaremos invariante fundamental.

Nos sirve ante todo para determinar la unidad de longitudes y tiempos en cualquier sistema de referencia S.

Para ello debemos inquirir todos los puntos universales para los cuales G tiene el valor +1 ó -1.

Evidentemente es G = 1 para el punto universal x = 1, t = 0; es éste, empero, el punto final de una unidad de medida a partir del punto cero del sistema de referencia S en el momento t = 0. Como vale de igual manera para todos los sistemas de referencia S, reconocemos, pues, que los puntos universales, para los cuales G = 1 definen la unidad de longitud en reposo, para cualquier sistema de referencia, como vamos a explicar en seguida con más detenimiento.

Igualmente es G = -1 para el punto universal x = 0, t = ${\tfrac {1}{c}}$; este punto universal está en conexión por modo correspondiente con la unidad de tiempo del reloj en reposo en el sistema S.

Los puntos G = +1 ó G = -1 pueden construirse geométricamente con gran facilidad partiendo del sistema de coordenadas invariantes ξη. El eje ξ está formado por los puntos para los cuales η = 0; por otra, esos mismos puntos caracterízanse en un sistema inercial S cualquiera porque x = ct. Por lo tanto, η debe ser proporcional a x - ct; si elegimos convenientemente la unidad de η podemos establecer:

$\eta =x-ct.$

De igual manera hallamos, considerando el eje η, que se puede establecer

$\xi =x+ct$

y entonces:

$\xi \eta =(x-ct)(x+ct)=x^{2}-c^{2}t^{2}=G$

fig112

G = ξη significa evidentemente el contenido de un rectángulo de lados ξ y η; si se quiere hallar un punto universal para el cual G = ξη = 1, bastará poner cuidado en que el rectángulo formado con las coordenadas ξη tenga el contenido superficial 1. Todos esos rectángulos pueden conocerse; entre ellos está el cuadrado de lado 1, y los demás son tanto más altos cuanto más estrechos son, y tanto más bajos cuanto más anchos, correspondiendo a la condición $\eta ={\tfrac {1}{\xi }}$ (fig. 112). Los puntos ξ, η forman, evidentemente, una curva que va acercándose cada vez más al eje ξ y al eje η; esa curva se llama hipérbola equilátera. Si ξ y η son ambos negativos, entonces ξ·η es positivo; por tanto, la construcción da, en el cuadrante de enfrente, otra rama de hipérbola simétrica a la anterior.

Para G = -1 rige la misma construcción en los otros dos cuadrantes, en donde las coordenadas ξ y η, tienen diferente signo.

Las cuatro hipérbolas forman las buscadas Curvas de estimación que establecen las unidades para longitudes y tiempos en todos los sistemas de referencia xt.

fig113

El eje x atraviesa las ramas de la hipérbola G = +1 en los puntos P y P'; el eje t atraviesa las ramas de la hipérbola G = -1 en Q y Q' (figura 113).

Por P trazamos una paralela al eje t, y decimos que esta paralela no vuelve a tocar un segundo punto de la rama derecha de la hipérbola G = +1, sino solamente el punto P. Dicho de otro modo: afirmamos que no hay un solo punto de esa rama de la hipérbola que esté a la izquierda de la recta, sino que la rama entera está a la derecha de ella, esto es, que todos los puntos de esta rama de la hipérbola tienen coordenadas x mayores todas que la distancia OP.

Y efectivamente así es. Pues para cada punto de la curva $G=x^{2}-c^{2}t^{2}=1$ será $x^{2}=1+c^{2}t^{2}$. De suerte que para el punto P de la curva, que se encuentra también en el eje x, esto es, en t = 0, resultará x² = 1; pero para cualquier otro punto de la curva será x² > 1 en la cantidad positiva c²t². Por lo tanto, OP = 1, y para cualquier otro punto de la rama derecha de la curva será x mayor que 1.

De igual manera se sigue que la paralela trazada por P' eje t toca la rama izquierda de la hipérbola G = 1 en P' y que las paralelas trazadas por Q y por Q' al eje x tocan en Q y en Q' las ramas de la hipérbola G = -1. La distancia OQ es, evidentemente, = ${\tfrac {1}{c}}$; pues el punto Q está en la curva $G=x^{2}-c^{2}t^{2}=-1$, y también en el eje t; esto es, x = 0, siendo, pues, para él $c^{2}t^{2}=1,\ t={\tfrac {1}{c}}$.

Las dos paralelas al eje t por P y P' cortan las líneas luminosas ξ, y η, en los puntos R y R'; por los mismos puntos pasan, empero, también las paralelas al eje x por Q y Q'. Pues vale, por ejemplo, para el punto R la ecuación x = ct, porque R está en el eje ξ y también x = 1, porque esta en la paralela al eje t por P; de aquí se sigue que $t={\tfrac {1}{c}}$, es decir, que está en la paralela al eje x por Q.

Se ve, pues, que esta construcción del eje x concuerda con la dada anteriormente de los puntos universales simultáneos (pág. 258). Pues la resta OQ en el eje t y las dos paralelas PR y P'R' son las líneas universales de tres puntos, uno de los cuales, O, está en el centro de los otros dos, P, P'; si de O parte una señal luminosa hacia ambos lados, quedará representada por las lineas luminosas ξ, η, y alcanzará las dos líneas universales externas en R y R'. Por consiguiente, esos dos puntos universales son simultáneos; la línea que los une es paralela al eje x, exactamente como nuestra nueva construcción lo ha realizado.

Resumiremos el resultado de esta reflexión:

Los ejes x y t de un sistema de referencia S son uno a otro de suerte que cada uno de ellos es paralelo a aquella recta que toca a la curva en el punto de intersección con el otro eje.

La unidad de longitud está representada por la distancia OP; la unidad de tiempo está determinada por la distancia OQ, que significa desde luego no 1 sec, sino ${\tfrac {1}{c}}sec.$

Toda línea universal que toque a la curva G = 1 puede ser tomada como eje x, y entonces queda establecido el eje t como paralelo a la recta que toca en P. De igual modo puede el eje t ser elegido como una línea universal cualquiera que toque a la curva G = -1, y entonces el correspondiente eje x queda determinado unívocamente por la construcción análoga.

Estas reglas vienen a substituir las leyes de la cinemática clásica; en éstas el eje x era el mismo para todos los sistemas inerciales, la unidad de longitud estaba dada fijamente en él y la unidad de tiempo era igual a la sección sobre el eje t, en general oblicuo, hecha por una recta determinada, paralela al eje x (véase pág. 88, fig. 37).

¿Cómo es, pues, que esas al parecer tan distintas construcciones son en realidad apenas discernibles?

fig114

Ello obedece al enorme valor de la velocidad de la luz c, si se mide en centímetros y segundos. En efecto; si en la figura queremos representar 1 sec. y 1 cm. por distancias de igual longitud, habrá que reducir el dibujo en la dirección t, de manera que todas las distancias paralelas al eje t se compriman en la relación 1:c. Si c fuese igual a 10, resultaría una imagen como la que presenta la figura 114; las dos líneas luminosas formarían un ángulo agudísimo que representa el espacio dentro del cual juegan los ejes x; en cambio, el ángulo que queda para los ejes t sería muy grande; y cuanto mayor sea c, tanto más resaltaría la diferencia cuantitativa de variabilidad entre la dirección x y la t. Para el valor real de c, que es 3·10¹⁰ centímetros/sec., no podría hacerse el dibujo en el papel; las dos líneas luminosas coincidirían prácticamente, y la dirección x, que cae siempre entre ellas, sería, pues, constante. Esto es justamente lo que admite la cinemática corriente; se ve, pues, que ésta es un caso especial o, mejor dicho, un caso límite de la cinemática de Einstein, a saber: el caso límite de una velocidad de la luz infinitamente grande.

4. Metros y relojes en movimiento.

Vamos ahora a resolver los sencillos problemas cinemáticos que se refieren al juicio de las longitudes de uno y el mismo metro, y de una y la misma duración en diferentes sistemas de referencia.

Una vara de longitud 1 se coloca a partir del punto O del sistema S, a lo largo del eje x; queremos saber su longitud en el sistema S'. Es claro que esta longitud no será igualmente 1; pues los observadores arrastrados en el movimiento de S' medirán simultáneamente las posiciones de los puntos extremos de la vara, es decir, simultáneamente en el sistema de referencia S'. Pero esto no es simultáneamente en el sistema de referencia S; así, aun cuando la posición de un extremo de la vara sea leída simultáneamente en S y S', la posición del otro extremo no lo será simultáneamente por los observadores de los sistemas S y S' respecto del tiempo de S; entretanto el sistema S' se ha desplazado, la lectura de los observadores S' refiérese, pues, a una posición desplazada del otro extremo de la vara.

La cosa parece a primera vista complicada desesperadamente. Hay enemigos del principio de relatividad, espíritus simples que, cuando oyen expresar esta dificultad de medir una vara, exclaman indignados: «¡Claro, con relojes descompuestos puede deducirse todo! Se ven en esto los absurdos a que conduce la fe ciega en el mágico poder de las fórmulas matemáticas.» Y dicho esto, condenan en bloque la teoría de la relatividad. Los lectores de nuestra exposición habrán comprendido seguramente que las fórmulas no son lo esencial, sino que se trata de puras relaciones de concepto, que pueden entenderse muy bien sin matemáticas. Es más: podría renunciarse, en el fondo, no sólo a las fórmulas, sino hasta a las figuras geométricas, y expresarlo todo en las palabras del lenguaje corriente; pero el libro resultaría entonces tan voluminoso y falto de claridad, que no habría editor que lo imprimiese ni lector que lo estudiase.

fig115

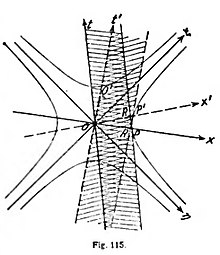
Emplearemos primero nuestra figura en el plano xt, para resolver el problema de determinar la longitud de la vara en los dos sistemas S y S' (fig. 115).

La vara está inmóvil en el sistema S(x, t); por lo cual la línea universal de su punto inicial es el eje t, y la de su punto terminal, la paralela a aquélla a la distancia 1; ésta toca a la curva en el punto P. La vara queda, pues, representada, para todos los tiempos, por la franja entre esas dos rectas.

Ahora debemos determinar su longitud en el sistema S'(x't'), que se mueve con respecto a S; el eje t' está inclinado con respecto al eje t. Encontramos el correspondiente eje x', trazando, por el punto Q' de intersección entre el eje t' y la curva, la tangente a ésta, y por el punto O la paralela a esta tangente, OP'. La distancia OP' es la unidad de longitud en el eje x'. La longitud de la vara unidad, que se halla en reposo en el sistema S, es determinada, si se mide en el sistema S', por la distancia OR', que, en la franja de paralelas representante de la vara, recorta el eje x'; pero esta distancia es evidentemente más corta que OP' y, por lo tanto, es OR' más pequeño que 1: la vara aparece disminuida en el sistema S' en movimiento.

Es ésta exactamente la contracción ideada por Fitz-Gerald y Lorentz para explicar el experimento de Michelson, preséntase aquí como consecuencia natural de la cinemática de Einstein.

Si, inversamente, una vara en reposo en el sistema S' es medida desde el sistema S, aparecerá naturalmente también disminuida; no se crea que aumentada; pues la tal vara queda representada por la franja limitada por el eje t' y la línea universal, paralela a este eje t' y que pasa por el punto P'; esta línea corta, empero, la distancia unidad OP del sistema S en un punto interior R, de suerte que OR es más pequeño que 1.

La contracción es, pues, completamente recíproca, como lo exige el principio de relatividad.

La magnitud de la contracción hallámosla fácilmente por la transformación de Lorentz [65].

Sea l la longitud de la vara en el sistema de referencia S, en la cual está en reposo; llámase a l también la longitud inmóvil o longitud propia de la vara.

Si ahora establecemos la longitud de la vara, tal como se juzga desde el sistema S', habrá que poner t' = 0, lo cual expresa que las lecturas de la posición de los dos puntos extremos de la vara, con respeto a S', son simultáneas. Y entonces, por la última ecuación de la transformación de Lorentz [fórmula 65] se sigue:

$t={\frac {v}{c^{2}}}x;$

y si se incluye ésta en la primera, se obtiene:

$x'={\frac {x-vt}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {x-{\frac {v^{2}}{c^{2}}}x}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=x{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

Pero para el punto inicial de la vara es x = 0, y, por tanto, también x' = 0; para el punto terminal es x = l; y si x' = l' significa la longitud de la vara medida en el sistema S', se obtendrá:

$l'=l{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$[67]

Esto significa que la longitud de la vara en el sistema S' parece disminuida en la relación ${\sqrt {1-\beta ^{2}:1}}$, en exacta coincidencia con la hipótesis de la contracción de Fitz-Gerald y Lorentz (V, 15, pág. 240).

Las mismas reflexiones valen para la determinación de una duración en dos distintos sistemas S y S'.

fig116

Imaginemos relojes regulados en todos los puntos del espacio en el sistema S. Estos relojes tienen, simultáneamente, una determinada señal de las manecillas con referencia a S; la posición t = 0 queda representada por los puntos universales del eje x; la posición

$t={\frac {1}{c}}$

queda representada por los puntos universales de la recta paralela al eje x, que pasa por el punto Q (figura 116).

En el punto cero del sistema S' ponemos un reloj que, para t = 0, señala también t' = 0; queremos saber qué posición tendrán sus manecillas cuando el reloj del sistema S, que se halla en el mismo sitio, señale exactamente t=\frac{1}{c}. Debemos recordar que el sistema S' entretanto se ha movido hacia adelante; el deseado valor de t' es evidentemente el punto de intersección R' del eje t' con la paralela al eje x que pasa por Q. Como ésta toca la curva G = —1, el punto R' está dentro de la distancia OQ' siendo Q' la intersección del eje t' con la curva; esto significa, empero, que la unidad de tiempo del sistema S aparece reducida en el sistema S'.

Para establecer el valor de esa reducción, pongamos en la transformación de Lorentz, para el reloj que se encuentra en el punto cero de S', x' = 0, es decir, = vt; tendremos entonces:

$t'={\frac {t-{\frac {v}{c^{2}}}x}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=t{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$[68]

Esta reducción de la unidad de tiempo es, pues, igual a la contracción de la longitud.

Naturalmente, la unidad de tiempo de un reloj en reposo en el sistema S aparecerá inversamente reducida también en el sistema S'.

Puede decirse también que, juzgados desde un sistema cualquiera, los relojes de todo sistema que se mueva con respecto del anterior, parecen retrasar. Los cursos del tiempo en sistemas movidos unos con relación a otros son mas lentos; todos lo procesos en esos sistemas retrasan con respecto a los procesos correspondientes del sistema considerado como inmóvil. Volveremos luego sobre las circunstancias que de aquí se derivan y que muchas veces se califican de paradojas.

Los datos de un reloj en el sistema de referencia en que está el reloj quieto llámanse tiempo propio del sistema. Es éste idéntico al tiempo local de Lorentz; el progreso de la teoría de Einstein no se refiere a las leyes formales, sino más bien a su concepción fundamental. En la teoría de Lorentz aparece el tiempo local como un artificio matemático, en oposición al tiempo verdadero, absoluto. Einstein ha establecido que no existe medio alguno de determinar ese tiempo absoluto, de extraerlo de los tiempos locales, infinitamente numerosos, y todos igualmente lícitos, de los distintos sistemas de referencia en movimiento. Esto significa, empero, que el tiempo absoluto no tiene realidad física; los datos del tiempo sólo tienen sentido con relación a determinados sistemas de referencia. Así queda realizada la relativización del concepto de tiempo.

5. Apariencia y realidad.

Ahora, ya que conocemos las leyes de la cinemática de Einstein, en la doble especie de figuras y de fórmulas, debemos aclararlas brevemente desde el punto de vista de la teoría del conocimiento.

Podría llegarse efectivamente a la opinión de que en la teoría de Einstein no se trata de nuevos conocimientos sobre las cosas del mundo físico, sino sólo de definiciones de índole convencional que, si bien concuerdan con las exigencias empíricas, podrían, sin embargo, ser substituidas por otras determinaciones. Este pensamiento se ofrece naturalmente si pensamos en el punto de partida de nuestras consideraciones, aquel ejemplo del tren de remolque, en donde salta a la vista lo convencional y caprichoso de la definición que da Einstein de la simultaneidad. Efectivamente, la cinemática toda de Einstein podría desenvolverse íntegramente para barcos que se muevan estando el aire en calma, haciendo uso de señales acústicas; la magnitud c significaría en todas las fórmulas la velocidad del sonido. Todos los barcos en movimiento tendrían, pues, cada cual, según su velocidad, sus unidades propias de medida y de tiempo, y entre los sistemas de medida, usados por los diferentes buques, valdrían las transformaciones de Lorentz; obtendríase, en pequeño, un mundo a la Einstein, coherente y libre de contradicciones.

Pero esta coherencia mantiénese sólo mientras admitimos que las unidades de longitud y de tiempo no han de ser limitadas por ninguna otra condición que la vigencia de los dos principios, el de relatividad y el de la constancia de la velocidad del sonido o de la luz, respectivamente. ¿Es éste el sentido de la teoría de Einstein?

De seguro que no. Más bien establece el supuesto tácito de que una vara que en dos sistemas de referencia S y S' está reducida con respecto a ellos a las mismas condiciones físicas, por ejemplo, substraída a la acción de todas las fuerzas, representa ambas veces la misma longitud. Un metro en reposo en el sistema S y de longitud 1 debe tener, naturalmente, también en el sistema S' la longitud 1, si está en él en reposo y si se tiene cuidado de que las demás relaciones físicas (gravedad, temperatura, campos eléctricos y magnéticos) sean en S' en lo posible las mismas que en S. Otro tanto se exigirá para los relojes.

Podría llamarse esta suposición tácita de la teoría de Einstein el «principio de la identidad física de las unidades».

Tan pronto como se concibe este principio, se ve que la traslación de la cinemática de Einstein al caso de los barcos y a la comparación de los relojes con señales acústicas está en contradicción con él. Pues las unidades de longitud y de tiempo determinadas según precepto de Einstein merced a la velocidad del sonido no serán naturalmente iguales a las unidades de longitud y tiempo medidas con metros rígidos y relojes corrientes; las primeras no sólo son distintas en cada barco en movimiento, según la velocidad del mismo, sino que, además, la unidad de longitud es distinta cuando se coloca a lo largo del barco o en dirección perpendicular a su movimiento. La cinemática de Einstein sería, pues, una definición posible, si; pero en este caso ni siquiera sería útil; los metros y los relojes corrientes serían, sin duda alguna, muy superiores.

Por el mismo motivo resulta muy difícil hacer la cinemática de Einstein intuitiva por medio de modelos. Estos reproducen, ciertamente, con exactitud las relaciones entre longitudes y tiempos en distintos sistemas; pero hállanse en contradicción con el principio de la identidad de las unidades; la escala de longitudes debe elegirse justamente distinta en dos sistemas S y S' del modelo, en movimiento relativo uno a otro.

Muy distinto es lo que sucede en el mundo real según Einstein; aquí vale la nueva cinemática cuando se emplea para la determinación de las longitudes y los tiempos el mismo metro y el mismo reloj primero en el sistema S y luego en el sistema S'. Con esto elévase la teoría de Einstein sobre el punto de vista de una simple convención y llega a afirmar determinadas propiedades de los cuerpos reales; sólo así adquiere la significación fundamental para toda la concepción de la naturaleza.

Esta importante circunstancia se manifiesta con suma claridad cuando se considera el método de Römer para medir la velocidad de la luz por medio de los satélites de Júpiter. El sistema solar se mueve con relación a las estrellas fijas; si pensamos un sistema de referencia S firmemente unido a las estrellas fijas, entonces el Sol con sus planetas define otro sistema S'. Júpiter con sus satélites es un reloj (de bondad ideal); este reloj se mueve en círculo, de suerte que unas veces se halla en la dirección del movimiento relativo de S' con respecto a S y otras en la dirección opuesta. La marcha del reloj-Júpiter en esas posiciones no puede determinarse caprichosamente por convención; de suerte que el tiempo que necesita la luz para recorrer el diámetro de la trayectoria de la Tierra sea igual en todas las direcciones, sino que ello es así por sí mismo, merced a la disposición del reloj-Júpiter. Este señala justamente el tiempo propio del sistema solar S', no un tiempo absoluto ni el otro tiempo del sistema S de las estrellas fijas; dicho de otro modo, el tiempo de revolución de los satélites de Júpiter es constante relativamente al sistema solar (en lo cual se prescinde de la velocidad de Júpiter mismo relativamente al sistema solar).

Ahora bien; algunos sostienen que esta concepción significa una lesión a la ley de causalidad. En efecto; si uno y el mismo metro juzgado desde el sistema S tiene longitud diferente según que esté en reposo en S o se mueva relativamente a S, tiene que existir, dicen, una causa de tal modificación; ahora bien, la teoría de Einstein no indica causa alguna, sino que afirma que la contracción se produce por sí misma, como circunstancia concomitante del hecho del movimiento. Mas esta objeción no esté justificada; obedece a una estrechísima concepción del concepto de «modificación». En sí carece de sentido tal concepto; no significa nada absoluto, como tampoco los datos de magnitud y de tiempo tienen una significación absoluta. Cuando un cuerpo se mueve en linea recta y uniformemente con respecto a un sistema inercial S, nadie piensa en decir que «sufra una modificación», aun cuando su lugar se modifica y varía con respecto al sistema S. ¿Qué «modificaciones» considera la física como efectos para los cuales hay que buscar causas? Ello no es a priori claro, sino que la investigación empírica misma lo determina.

La concepción de la teoría de Einstein sobre la esencia de la contracción es la siguiente:

fig117

Una vara material no es físicamente una cosa espacial, un trozo de espacio, sino un complejo de espacio y tiempo; cada punto de la vara es ahora y ahora y ahora y sigue siendo en todo tiempo. La imagen adecuada de la vara referida (unidimensional en el espacio) no es, pues, una distancia en el eje x, sino una franja en el plano xt (figura 117). La misma vara en reposo en diferentes sistemas S y S' que se mueven, será representada por diferentes franjas. No existe a priori ninguna regla que disponga cómo han de dibujarse esos complejos duodimensionales del plano xt, para que representen exactamente el modo de comportarse físicamente una y la misma vara en diferentes velocidades. Para ello hay que empezar por establecer en el plano xt una curva estimativa. La cinemática clásica dibuja esta curva de distinta manera que Einstein; quién tenga razón es cosa que no puede decidirse a priori. En la teoría clásica las dos franjas tienen la misma anchura, medida paralelamente a un eje firme x; en la teoría de Einstein tienen la misma anchura, medida en las distintas direcciones x de los sistemas de referencia en movimiento relativo, con distintas pero determinadas unidades. La «contracción» no se refiere a la franja, sino a la distancia recortada por un eje x; pero realidad física sólo la tiene la franja como multiplicidad de puntos universales, sucesivos, y no la tiene la sección. La contracción es, pues, sólo una consecuencia del modo de considerar las cosas; no es una modificación de una realidad física; no cae, pues, bajo los conceptos de causa y efecto.

Esta concepción resuelve la cuestión, ya tocada por nosotros, de si la contracción es «real» o «aparente». Si yo corto una rueda de salchichón, ésta será mayor o menor según que la corte inclinando mas o menos el cuchillo. Es absurdo llamar «aparentes» las distintas magnitudes de la rueda de salchichón y calificar de magnitud «real», por ejemplo, la más pequeña, la que procede de un corte perpendicular.

Del mismo modo, una vara, en la teoría de Einstein, tiene longitudes distintas según el punto de vista del observador; una de ellas es la máxima, la longitud en reposo; pero no por eso es más real que las otras. Aplicar en este sentido ingenuo la disyuntiva: «aparente» o «real», no es más sensato que preguntar por la verdadera coordenada x de un punto x y, sin indicar previamente el sistema de coordenadas x y a que se refiere.

Otra tanto puede decirse de la relatividad del tiempo. Un reloj ideal tiene siempre una y la misma marcha en el sistema de referencia en donde se halla en reposo; señala el «tiempo propio» del sistema de referencia. Pero, juzgado desde otro sistema de referencia, anda más despacio; un determinado espacio del tiempo local aparece allá más largo. También aquí es absurdo preguntar cuál sea la «real» duración de un proceso.

Comprendida rectamente, la cinemática no contiene ni obscuridades ni contradicciones internas. Sin duda, muchos de sus resultados están en oposición con hábitos mentales o con teorías de la física clásica. Cuando esas oposiciones son particularmente violentas, parecen frecuentemente insoportables y paradójicas. En lo sucesivo sacaremos de la teoría de Einstein numerosas conclusiones que fueron recibidas al principio con ruda oposición hasta que se consiguió confirmarlas experimentalmente. Pero aquí queremos comunicar una reflexión que conduce a resultados particularmente extraños, sin que parezca posible comprobarlos por medio de experimentos; trátase de la llamada paradoja de los relojes.

Imaginemos un observador A inmóvil en el punto cero del sistema inercial S. Un segundo observador B se encuentra primeramente en el mismo sitio O, en reposo, pero luego se mueve con velocidad uniforme en línea recta sobre el eje c por ejemplo, hasta llegar a un punto C, en donde da la vuelta y regresa en línea recta y con la misma velocidad que antes al punto O.

fig118

Ambos observadores llevan consigo relojes ideales, que señalan su tiempo propio. El tiempo de la aceleración al arrancar, al dar la vuelta y al llegar B al término de su viaje, pueden reducirse cuanto se quiera con relación a la duración total del viaje, haciendo que la duración de los movimientos uniformes a la ida y a la vuelta sea suficientemente grande; por si acaso la marcha de los relojes hubiese de sufrir la influencia de la aceleración, podrá reducirse relativamente cuanto se quiera este efecto, alargando lo bastante la duración del viaje, de suerte que pueda el efecto de la aceleración despreciarse. Pues bien; el reloj del observador B, a su regreso a O, debe retrasar con respecto del reloj de A; pues sabemos (VI, 4, pág. 270) que durante los periodos del movimiento uniforme de B, que son decisivos para el resultado, el tiempo propio retrasa con relación al tiempo de cualquier otro sistema inercial. Se ve esto intuitivamente en la imagen geométrica del plano xt (figura 118.) En esta figura, para mayor comodidad, hemos dibujado los ejes del sistema xt perpendiculares. La línea universal del punto A es el eje t; la línea universal del punto B es la quebrada (dibujada con puntos) OUR, cuyo vértice U hállase sobre la línea universal del punto de retorno, que es una línea paralela al eje t.

Pasemos por U la hipérbola que se deriva de la curva estimativa G = —1 agrandándola en correspondencia; esta hipérbola corta el eje t en Q. Entonces, evidentemente, la distancia del tiempo propio OQ para el observador A es exactamente igual a la distancia del tiempo propio OU para el observador B. La duración del tiempo propio para A hasta el retorno al punto de partida R es, empero, como muestra la figura, más del doble de OQ, mientras que para B es exactamente el doble de OU. Por tanto, el reloj de A, al momento del regreso, estará adelantado sobre el de B.

La magnitud del adelanto se calcula fácilmente por la fórmula [68], en donde t significa el tiempo propio de A y t' el de B. Si nos limitamos a pequeñas velocidades de B y consideramos $\beta ={\tfrac {v}{c}}$ como número pequeño, podremos, en lugar de la fórmula [68], escribir aproximadamente:

$t'=t\left(1-{\frac {1}{2}}\beta ^{2}\right);$

por donde el adelanto del reloj de A sobre el de B es:

$t-t'={\frac {\beta ^{2}}{2}}t,$[69]

y esta fórmula vale en todo momento del movimiento, pues la ida y la vuelta se verifican con la misma velocidad; vale particularmente también para el momento del regreso, siendo t la duración total del viaje según el tiempo propio de A, y t' la duración del viaje según el tiempo propio de B.

Lo paradójico de este resultado obedece a que todo proceso interior en el sistema B debe verificarse más lentamente que el mismo proceso en el sistema A. Todas las vibraciones atómicas, y aun el curso mismo de la vida, deben comportarse como los relojes; si, pues, A y B son hermanos gemelos, será B, a la vuelta de su viaje, más joven que A. En realidad, es ésta una conclusión extraña, pero que ninguna interpretación capciosa puede evitar. Hay que conformarse, como hace algunos siglos hubieron de conformarse los hombres con los antípodas cabeza abajo; como se trata, según lo demuestra la fórmula [69], de un efecto del segundo orden, difícilmente podrán deducirse de él consecuencias prácticas.

Al ponernos en guardia contra este resultado, y al llamarlo paradoja, no queremos decir otra cosa sino que es «extraño», «poco habitual»; pero el tiempo nos ayudará a tolerarlo. Pero todavía existen enemigos de la teoría de la relatividad que quieren inferir de esta reflexión una objeción contra la consecuencia interna lógica de la teoría. Arguméntase del modo siguiente: según la teoría de la relatividad, los sistemas que se mueven uno con respecto a otro, son igualmente legítimos. Se puede, pues, considerar también B como inmóvil; entonces A realiza un viaje en la misma forma exactamente que lo realizó B antes, sólo que en dirección opuesta. Hay que concluir, por tanto, que el reloj de B, al regresar A de su viaje, va adelantado con respecto al reloj de A. Pero antes habíamos llegado exactamente al resultado contrario. Como no es posible que el reloj de A esté adelantado sobre el de B y el de B esté adelantado sobre el de A, adviértese aquí una contradicción interna de la teoría. Así opinan los superficiales. El error de esta objeción es patente; el principio de relatividad refiérese solamente a sistemas en movimiento uniforme y rectilíneo unos con respecto de otros; no es aplicable, en la forma que hasta ahora llevamos desarrollada, a sistemas acelerados. Pero el sistema B es acelerado; no es, pues, igualmente válido que A. A es un sistema inercial; B no lo es. Luego hemos de ver, sin duda, que la teoría general de la relatividad de Einstein considera como equivalente también los sistemas acelerados unos con respecto de otros; pero lo hace en un sentido que necesita exacta explicación; desde este punto de vista general, habremos de volver sobre la «paradoja de los relojes» y demostraremos que tampoco hay aquí, si bien se reflexiona, ninguna dificultad.

La relativización de los conceptos de longitud y duración parece difícil a muchos; sin embargo, sólo es porque no se han acostumbrado a ella. La relativización de los conceptos de «arriba» y «abajo» por el descubrimiento de la forma esférica de la Tierra, no habrá originado seguramente menos dificultades a los hombres de aquel tiempo. También en este caso el resultado de la investigación contradecía una intuición oriunda del inmediato vivir psíquico. De igual manera la relativización del tiempo por Einstein parece no estar en corcordancia con la intuición individual del tiempo, pues el sentimiento del «ahora» se extiende sin límites sobre el universo, enlazando todo el ser con el yo. Que lo que el yo siente como «simultáneo», haya de caracterizarlo otro como «sucesivo», es cosa que, en realidad, no se concibe por medio de la intuición del tiempo. Pero la ciencia exacta tiene otros criterios de la verdad; puesto que la «simultaneidad» absoluta no es determinable, debe excluir ese concepto de su sistema.

6. La adición de las velocidades.

Ahora vamos a penetrar más profundamente en las leyes de la cinemática de Einstein. Nos limitaremos principalmente a la consideración del plano xt; la generalización de las leyes, así conseguidas, al espacio cuatridimensional xyzt no trae consigo dificultades esenciales, por lo cual sólo de pasada hablaremos de ella.

Las líneas luminosas, que se caracterizan por G = x² - c²t² = 0, dividen el plano xt en cuatro cuadrantes (fig. 119); en cada cuadrante conserva evidentemente G el mismo signo, siendo G > 0 en los dos cuadrantes opuestos que contienen los brazos de la hipérbola G = +1, y G < 0 en los dos cuadrantes opuestos que contienen los brazos de la hipérbola G= -1. Una línea universal recta que pase por el punto cero O puede ser eje x o eje t, según vaya por el cuadrante G > 0 ó por el G < 0; correspondiendo a lo cual distínguense las líneas universales en líneas universales de tiempo o temporales y líneas universales de espacio o espaciales.

fig119

En un sistema inercial cualquiera, el eje x separa los puntos universales «del pasado» (t < 0) de los puntos universales «del futuro» (t > 0). Pero para cada sistema inercial es la separación distinta; pues para otra posición del eje x, algunos puntos que antes estaban por encima del eje x, esto es, en el futuro, caen por debajo del eje x, esto es, en el pasado, y recíprocamente. Sólo los sucesos representados por puntos universales dentro de los cuadrantes G < 0 son para cada sistema inercial unívocamente o «pasados» o «futuros». Para tal punto universal P, es $t^{2}>{\tfrac {x^{2}}{c^{2}}}$, esto es, en cada sistema admisible de referencia es la duración de tiempo que separa los dos sucesos O y P mayor que el tiempo que la luz necesita para ir de uno a otro lugar. Se puede, pues, establecer siempre un sistema inercial tal, que su eje t pase por P, y en el cual P represente, por tanto, un suceso que se verifica en el punto cero de espacio; juzgado desde otro sistema inercial, moveráse ese sistema S rectilínea y uniformemente de tal manera, que su punto cero coincida exactamente con los sucesos O y P. Entonces para el suceso P en el sistema S será x = 0, esto es, G = -c²t² < 0.

En todo sistema inercial, el eje t separa los puntos universales, a los cuales corresponden sucesos que se hallan en el eje x «delante» o «detrás» del punto cero espacial. Pero para otro sistema inercial, con otro eje t, es evidentemente otra la separación; sólo para los puntos universales situados dentro de los cuadrantes G > 0 queda unívocamente determinado si están «delante» o «detrás» del punto cero espacial. Para uno de esos puntos , es $t^{2}<{\tfrac {x^{2}}{c^{2}}}$; es decir, que en todo sistema de referencia autorizado es el espacio de tiempo que separa dos sucesos O y P más pequeño que el tiempo que necesita la luz para ir de uno a otro. Entonces puede introducirse un adecuado sistema inercial en movimiento, cuyo eje x pase por P, siendo, pues, los dos sucesos O y P simultáneos. En este sistema es evidente que para el suceso P es t = o, esto es, G = x² > 0.

De aquí se deduce que la invariante G es para cada punto universal P una magnitud mensurable de significación intuitiva; o bien P y O «pueden transformarse al mismo lugar», y entonces G = -c²t², siendo t la diferencia de tiempo entre el suceso P y el suceso O que se halla en el mismo lugar del sistema S; o bien P y O pueden transformarse «a simultaneidad», y entonces G = x², siendo x la distancia espacial entre los dos sucesos simultáneos en el sistema S.

Las líneas de luz G = 0 representan en todo sistema de coordenadas movimientos con la velocidad de la luz. Por eso a toda línea universal de tiempo corresponde un movimiento de menor velocidad; todo movimiento con velocidad inferior a la de la luz puede «transformarse en reposo», porque pertenece a él una línea universal de tiempo.

Pero ¿y los movimientos con velocidad superior a la de la luz?

Según lo que antecede, está claro que la teoría de Einstein tiene que declarar imposibles físicamente tales movimientos. Pues la nueva cinemática pierde todo sentido si hubiese señales que permitieran comprobar la simultaneidad de dos relojes con velocidad superior a la de la luz.

Aquí parece surgir una dificultad.

Admitiendo que un sistema S' tenga la velocidad v respecto de otro sistema S, un cuerpo K se mueve relativamente a S' con la velocidad u'. Según la cinemática corriente, la velocidad del cuerpo K, relativamente a S, será:

$u=v+u'$

Si ahora tanto v como u' son mayores que la mitad de la velocidad de la luz, será u = v + u' mayor que c, cosa que, según la teoría de la relatividad, debe ser imposible.

Naturalmente, esta contradicción obedece a que en la cinemática del principio de relatividad, donde cada sistema de referencia tiene sus propias unidades de longitud y de tiempo, las velocidades no pueden sumarse sencillamente.

Ya se ve ello por el hecho de que, en cualesquiera sistemas de referencia en movimiento, la velocidad de la luz tiene siempre el mismo valor; justamente este hecho es el que hemos empleado antes para deducir la transformación de Lorentz (VI, 2, pág. 259), y la fórmula [63] establecida allí (pág. 260) da la ley exacta para la adición de las velocidades; bastará introducir en ella $\alpha ^{2}-1=\beta ^{2}={\tfrac {v^{2}}{c^{2}}}$. Preferimos, sin embargo, derivar una vez más esta regla de la transformación de Lorentz [65] (pág. 261); para lo cual dividiremos las expresiones de x' e y' (ó z') por las expresiones de t':

${\frac {x'}{t'}}={\frac {x-vt}{t-{\frac {v}{c^{2}}}x}},\quad {\frac {y'}{t}}={\frac {y{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}{t-{\frac {v}{c^{2}}}x}}.$

Si en estas ecuaciones abreviamos la parte de la derecha por medio de t, aparecerán los cocientes $u_{p}={\tfrac {x}{t}}$, $u_{s}={\tfrac {y}{t}}$, los cuales evidentemente son las proyecciones o componentes de la velocidad del cuerpo K, medidas en el sistema S y situadas paralela (longitudinal) y perpendicular (transversalmente) a la dirección del movimiento del sistema S' relativamente a S; los cocientes $u'_{p}={\tfrac {x'}{t'}}$, $u'_{s}={\tfrac {y'}{t'}}$ tienen la misma significación respecto del sistema S'. Obtiénese asi el teorema de la adición de las velocidades, de Einstein:

$u'_{p}={\frac {u_{p}-v}{1-{\frac {vu_{p}}{c^{2}}}}},\quad u'_{s}=u_{s}{\frac {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}{1-{\frac {vu_{p}}{c^{2}}}}},$[70]

que ocupa el lugar de la fórmula de la vieja cinemática:

$u'_{p}=u_{p}-v,\quad u'_{s}=u_{s}$

Si se trate especialmente de un rayo luminoso que va en la dirección del movimiento del sistema S' relativamente a S, será u_s = 0, u_p = c; y entonces la fórmula [70] da el resultado evidente

$u'_{p}={\frac {c-v}{1-{\frac {v}{c}}}}=c,\quad u'_{s}=0,$

que expresa la ley de la constancia de la velocidad de la luz. Pero además se ve que para un cuerpo cualquiera movido longitudinalmente es siempre u'_p < c, mientras sea u_p < c; pues si en la primera fórmula [70] se pone en lugar de u_p el valor mayor c, se agrandará el numerador y se disminuirá el numerador, de suerte que el quebrado aumentará, y tendremos:

$u'_{p}<{\frac {c-v}{1-{\frac {v}{c}}}},\$ o sea: $\ u'_{p}<c.$

Rige lo correspondiente para un movimiento transversal y, en general, para cualquier movimiento.

La velocidad de luz es, pues, cinemáticamente un limite infranqueable. Este afirmación de la teoría de Einstein ha sido muy combatida; parecía una injustificada limitación de futuros descubridores que quisieran buscar movimientos más veloces que el de la luz.

Conócese ya en los rayos β de las substancias radioactivas electrones que tienen casi la velocidad de la luz; ¿por qué no había de ser posible acelerarlos de suerte que llegasen a exceder la velocidad de la luz?

La teoría de Einstein afirma que eso no es posible, en principio; porque la resistencia de inercia o masa de un cuerpo es tanto mayor cuanto más su velocidad se acerca a la de la luz. Llegamos con esto a la nueva dinámica, que se construye sobre la cinemática de Einstein.

7. La dinámica de Einstein.

La mecánica de Galileo-Newton está estrechísimamente unida a la antigua cinemática; el principio clásico de relatividad se asienta principalmente en el hecho de que las modificaciones de velocidad, las aceleraciones, son invariantes frente a las transformaciones de Galileo.

Ahora bien; no cabe, naturalmente, admitir una cinemática para una parte del acaecer natural y otra para la otra parte; para la mecánica, la invariancia en las transformaciones de Galileo, y para la electrodinámica, la invariancia en las transformaciones de Lorentz.

Pero sabemos que las primeras son un caso límite de las segundas, cuando a la constante c se le da un valor infinito. Por eso admitiremos, con Einstein, que la mecánica clásica no tiene una validez estricta, sino que necesita modificarse; las leyes de la nueva mecánica deben ser invariantes frente a las transformaciones de Lorentz.

El establecimiento de estas leyes se verifica según un principio general, que conduce aquí, como en todos los problemas semejantes, a un resultado unívoco. Existe, en efecto, un sistema inercial S' en el que un cuerpo K, movido en cualquier modo, reposa en un determinado momento cualquiera. Se pedirá ahora que para ese sistema S' y ese momento valgan las leyes de la mecánica clásica, que ha de salir como caso límite de velocidades infinitamente pequeñas.

En el sistema S' valdrá, pues, la ley dinámica fundamental en la forma habitual (II, 10, pág. 48. Fórmula [7]).

$m_{0}b'=K'$[71]

en esta fórmula es m₀ una constante característica de la resistencia de inercia que tiene el cuerpo, la masa medida en el sistema en reposo S' o, más brevemente, la masa en reposo; b' es la aceleración con respecto a S', y K' es la fuerza que ésta produce, referida igualmente a S'.

Trátase ahora de trasladar esta ley del sistema de referencia especial S' atenido al movimiento del cuerpo, a un sistema de referencia cualquiera S. Realizaremos la transformación primero para la aceleración b' y luego para la fuerza K'.

Tenemos que distinguir también entre velocidad longitudinal y velocidad transversal, que designaremos por los índices p (paralela) y s (perpendicular).

Sea v la velocidad del sistema S' relativamente a cualquier otro determinado S. Como S' en el momento de la validez de la fórmula [71] tiene la misma velocidad que el cuerpo K y será para éste u_p = v y u_s = 0; entonces el teorema de la adición de las velocidades [70] (pág. 287) da el resultado trivial de u'_p = 0, u'_s = 0, que expresa la quietud de K relativamente a S'.

En un momento después, empero, ha recibido el cuerpo por la fuerza un aumento de velocidad longitudinal w_p y uno transversal w_s, de suerte que sus componentes de velocidad en el sistema S son:

$u_{p}=v+w_{p},\quad u_{s}=w_{s}$

Calculemos éstos, según el teorema de la adición [70], en el sistema S':

$u'_{p}={\frac {w_{p}}{1-{\frac {v}{c^{2}}}(v+w_{p})}},\quad u'_{s}=w_{s}{\frac {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}{1-{\frac {v}{c^{2}}}(v+w_{p})}}.$

Como antes de la impulsión era u'_p = 0 y u'_s = 0, son éstas expresiones al mismo tiempo las modificaciones de velocidad w'_p y w'_s; en el denominador puede abandonarse siempre w_p, porque este miembro daría sólo un añadido del segundo orden relativamente a w_p y w_s y, por división por el tiempo t, se obtiene

$b'_{p}={\frac {b_{p}}{1-{\frac {v^{2}}{c^{2}}}}},\quad b'_{s}={\frac {b_{s}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$[72]

Estas son las fórmulas de transformación de la aceleración.

Llegamos ahora a la consideración de la fuerza, y con ello a la explicación de una cuestión de principio.

fig120

Imaginemos, en efecto, los dos sistemas de coordenadas S y S' dibujados en el plano xt (fig. 120) y queremos ahora introducir en la figura la fuerza (o cualquier otra magnitud dirigida) como flecha. Como en el sistema S' ha de valer la mecánica corriente, habrá que dibujar la fuerza K' (o más exactamente su componente longitudinal K'_p) como una flecha en dirección del eje x'. Una mirada a la figura nos enseña al punto que esa flecha en el otro sistema tiene una proyección, no sólo en el eje x, sino en el eje t también. Así somos impelidos a la representación de que todas las magnitudes dirigidas o vectores no sólo tienen, como en la mecánica corriente, componentes espaciales, sino, en general, también temporales. Lo que estos últimos significan físicamente se ha de ver bien pronto; por ahora basta observar que sólo en el sistema inercial, en que el cuerpo considerado se halla en reposo, es donde falta el componente de tiempo.

Así, atribuiremos a la fuerza, además de un componente longitudinal K_p y dos componentes transversales K_z (uno por y y otro por z), un componente más de tiempo K_t. Por lo que se refiere al cálculo de esos componentes en distintos sistemas de referencia, nos apoyaremos en la observación de que la distancia de un punto al punto cero es también una magnitud dirigida y que todas las magnitudes dirigidas deben transformarse igual ^[1]; por lo tanto, igual se transformarán los componentes de una magnitud dirigida cualquiera que los componentes x, y, z, t de la distancia entre un punto y el punto cero, esto es, según las fórmulas de la transformación de Lorentz [65]. Obtiénese, pues:

$K'_{p}={\frac {K_{p}-vK_{t}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad K'_{s}=K_{s},\quad K'_{t}={\frac {K_{t}-{\frac {v}{c^{2}}}K_{p}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.$[73]

Pero en el sistema S' en movimiento será el componente K'_t = 0; de donde sigue:

$K_{t}={\frac {v}{c^{2}}}K_{p}$[74]

Esto demuestra que el componente de tiempo no tiene significación independiente, y que puede calcularse por los componentes longitudinales. Si se incluye su valor en la primera fórmula [73] se obtiene:

$K'_{p}=K_{p}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\quad K'_{s}=K_{s}.$[75]

Esta es la ley de la transformación de la fuerza.

Ahora las expresiones [72] y [75] pongámoslas en la fórmula [71], que afirma la validez de la mecánica corriente en el sistema S'; dividiéndolas en componentes paralelas y perpendiculares a la dirección del movimiento de S' relativamente a S, podemos escribir:

$m_{o}b'_{p}=K'_{p},\quad m_{0}b'_{s}=K'_{s}.$

Entonces obtenemos:

${\frac {m_{0}b_{p}}{\left({\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)^{3}}}=K_{p},\quad {\frac {m_{0}b_{s}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=K_{s}.$[76]

Estas son las fórmulas fundamentales de la dinámica de Einstein.

La conexión entre fuerza y aceleración producida es, pues, otra, según que la fuerza actúe en la dirección del movimiento, o en dirección perpendicular a él.

Suélense reducir estas fórmulas a una forma en que se parezcan lo mas posible a la ley fundamental de la dinámica clásica. Para ello se ponen:

$m_{p}={\frac {m_{0}}{\left({\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)^{3}}},\quad m_{s}={\frac {m_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},$[77]

dos magnitudes que se designan con el nombre de masa longitudinal y masa transversal; entonces puede escribirse:

$m_{p}b_{p}=K_{p},\quad m_{s}b_{s}=K_{s},$[78]

que coincide por la forma con la ley fundamental [7] de la mecánica ordinaria (II, 10, pág. 48).

Se ve aquí lo necesario que es definir desde el principio el concepto de masa exclusivamente por la resistencia de inercia; no sería posible de otro modo emplearlo en la mecánica relativista, pues para fuerzas longitudinales y transversales hay que tener en cuenta diferentes masas, y éstas no son, además, constantes características del cuerpo, sino que dependen de su velocidad. El concepto relativista de masa aléjase, pues, mucho del uso común del idioma, en el que masa significa algo así como cantidad de materia. Una medida de ésta es, en cierto modo, la masa en reposo m₀; pero ésta no es tampoco, como en la mecánica corriente, igual a la relación de la fuerza con la aceleración en cualquier sistema de referencia.

Ahora bien; las dos fórmulas [78] pueden aún reunirse en una que corresponde a otra concepción de la ley fundamental de la mecánica corriente. Allí (II, 9, pág. 45) habíamos visto que un cuerpo lleva consigo su impulsión mv y la cambia o comunica a otros cuerpos en sus acciones recíprocas; por lo cual cabe expresar la ley del movimiento de la manera siguiente:

Modificación temporal de la impulsión arrastrada = fuerza.

Nosotros afirmamos ahora que también aquí es posible esta concepción cuando la magnitud

$J=mv={\frac {m_{0}v}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$[79]

se define como impulsión arrastrada. Y entonces

$m={\frac {m_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$[80]

puede calificarse aquí simplemente como masa relativista; coincide con la masa transversal m_s.

Para demostrar este aserto, imaginemos que a la velocidad v se añade primero un pequeño aumento longitudinal w_p; entonces, por sencillo cálculo ^[2], es la modificación longitudinal de $J={\frac {m_{0}w_{p}}{\left({\sqrt {}}\right)^{3}}}$; luego añadimos a v un aumento transversal w_s y encontramos la modificación transversal de

$J={\frac {m_{0}w_{s}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.$

Si se divide ahora por el tiempo t de la modificación se obtienen justamente las dos mismas expresiones que según [76] son iguales a las fuerzas K_p y K_s.

¿Cuál es, pues, el más importante contenido de las nuevas leyes dinámicas? Una mirada a las fórmulas de las masas, [77] u [80], enseña que los valores de la masa relativista m (y, respectivamente, m_p y m_s) son tanto mayores cuanto más la velocidad v del cuerpo en movimiento se acerca a la velocidad de la luz. Para v = c la masa se hace infinitamente grande.

De aquí se infiere que es imposible, con fuerzas finitas, llevar un cuerpo a velocidad superior a la de la luz; la resistencia de inercia en el cuerpo crecería infinitamente y le impediría llegar a la velocidad de la luz.

Se ve por esto cómo la teoría de Einstein se redondea armónicamente para formar un todo unitario; el supuesto, paradójico al parecer, de una infranqueable velocidad límite es exigido por las leyes naturales mismas en su nueva forma.

La fórmula [80], que expresa cómo la masa depende de la velocidad, es la misma que Lorentz había encontrado, por cálculos electrodinámicos, para su electrón aplastado; en esos cálculos expresábase m₀ por la energía electrostática U del electrón en reposo, lo mismo que en la teoría de Abraham (V, 13, pág. 232, fórmula [62]), a saber:

$m_{0}={\frac {4}{3}}{\frac {U}{c^{2}}}$.

Vemos ahora que a la fórmula de las masas dada por Lorentz le conviene una significación mucho más general. Debe valer para toda especie de masas, sean o no de origen electromagnético.

Las recientes investigaciones sobre la desviación de los rayos catódicos parecen hablar en favor de la fórmula de Lorentz mejor que de la de Abraham. Pero una sorprendente confirmación de la fórmula relativista de la masa se ha conseguido en una esfera que parecía muy apartada de la teoría de la relatividad, es a saber: la espectroscopia de los rayos luminosos, de los rayos Röntgen.

Sólo podemos referirnos en breves palabras a estas relaciones admirables. La luminosidad de los átomos prodúcese porque los electrones, dentro de la reunión atómica, verifican movimientos vibratorios y hacen ondas electromagnéticas, que se propagan en todas las direcciones. La vieja teoría calculaba estos procesos por medio de las ecuaciones de Maxwell; pero recientemente se ha sentido la necesidad de renunciar a la validez estricta de esas ecuaciones en el interior de los átomos, y ha habido que admitir otras leyes que han sido introducidas por vez primera por Max Planck (1900) en la teoría de la irradiación térmica. Esta es la teoría llamada de los quanta. Niels Bohr (1913) ha utilizado esta teoría para la explicación del espectro, consiguiendo grandes éxitos. Sin entrar en detalles, observaremos solamente que, en movimientos rápidos de los electrones, la masa, según la teoría de la relatividad de Einstein, debe aumentar, y ello tendrá influencia en el espectro. Efectivamente, ha podido demostrar Sommerfeld (1915) que, a consecuencia de la variabilidad de las masas, las líneas espectrales tienen una estructura complicada; cada línea consta, en verdad, de todo un sistema de líneas más gruesas y más finas. En los espectros visibles, que son enviados por los electrones exteriores del átomo, es muy estrecho ese grupo de líneas y se trata de una «estructura fina»; en los espectros de Röntgen, que proceden del interior de los átomos, es una estructura grosera de escisión millones de veces mayor. La estructura fina de las líneas del espectro del hidrógeno y del helio, calculada por Sommerfeld, ha sido observada por Paschen (1916); también han tenido buen éxito estos ensayos en los espectros de Röntgen. Coinciden tan exactamente, que la diferencia entre las fórmulas de la masa dadas por Lorentz y por Abraham, que es una magnitud del segundo orden, entra en consideración; el discípulo de Sommerfeld, Glitscher, ha podido demostrar (1917) que la fórmula de Abraham es inconciliable con las observaciones en el espectro del helio; pero que la de Lorentz concuerda bien. Puede decirse, por tanto, que hay una confirmación espectroscópica de la teoría de la relatividad de Einstein.

Ya que toda masa depende de la velocidad, según la fórmula [80], resulta falsa la demostración de la naturaleza electromagnética de la masa del electrón, y por ende también de la conexión entre masa en reposo y energía electrostática. La teoría de Lorentz sobre el éter inmóvil pudo hacer el ensayo de reducir la inercia de las masas mecánicas a la característica facultad de permanencia que posee el campo eléctrico; si la teoría de la relatividad de Einstein se ve precisada a renunciar a tan magno plan, ¿no será esto motivo para que se lo reproche todo aquel que aspire a ver establecida la unidad de la naturaleza? Pero la nueva dinámica no falla aquí tampoco, sino que da la más profunda explicación sobre la esencia de la masa inerte.

8. La inercia de la energía.

Para todos los fines prácticos, y aun para los más veloces electrones, basta escribir las fórmulas de las masas hasta los miembros del segundo orden. Ahora bien; ya hemos visto antes (pág. 237, nota) que, con tal aproximación, es

${\frac {1}{\sqrt {1-\beta ^{2}}}}=1+{\tfrac {1}{2}}\beta ^{2}$;

por donde

$m=m_{0}\left(1+{\tfrac {1}{2}}{\frac {v^{2}}{c^{2}}}\right)$.

En la mecánica corriente queda definida la energía cinética (II, 14, pág. 61) por $T=m_{0}{\tfrac {v^{2}}{2}}$; según nuestra fórmula, tendrá la expresión

$T=c^{2}(m-m_{0})$

Puede demostrarse que esta definición de la energía cinética es estrictamente válida, aun cuando no se desprecien los miembros de más del segundo orden.

La ley de la energía (II, 14, fórmula [13], pág. 61) exige que la modificación temporal de la energía E = T + U durante el movimiento sea continuamente nula. En esto habrá que poner aquí, en lugar del valor clásico $T={\tfrac {m}{2}}v^{2}$, el valor relativista

$T=c^{2}(m-m_{0})=c^{2}m_{0}\left({\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\right);$[81]

si se forma con éste la modificación temporal, se obtendrá por un cálculo semejante ^[3] al anterior (véase pág. 293, nota) para aceleración longitudinal:

${\text{modificación temporal de }}T={\frac {m_{0}vb_{p}}{\left({\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)^{3}}}=K_{p}v,$[82]

donde se ha introducido el componente de fuerza longitudinal según la fórmula [76] (pág. 292). El lado derecho es, empero, la modificación temporal negativa de la energía potencial U. Pues durante un intervalo de tiempo t, suficientemente pequeño, se puede considerar la fuerza como aproximadamente constante y proceder como si se tratase de la gravedad, cuya energía potencial era igual a Gx (II, 14, fórmula [12] pág. 59); la dirección x fué entonces admitida como contraria a la gravedad, de suerte que puede ponerse G = -K_p. La modificación temporal de la energía potencial es entonces:

$G{\frac {x}{t}}=-K_{p}v$.

Por tanto, la ecuación [82] expresa, efectivamente, que la magnitud E = T + U es constante en el tiempo, donde T significa la expresión [81].

Ahora ya se conoce la significación física de los componentes de tiempo de la fuerza K_t; ésta, según la fórmula [74] está en conexión con el componente longitudinal por la ecuación

$K_{t}={\frac {v}{c^{2}}}K_{p}$.

El lado derecho es, según la fórmula [82], igual a la velocidad de variación de la energía cinética T dividida por c² es, pues, esta misma,

${\frac {T}{c^{2}}}=K_{t}t$,

donde t es el pequeño intervalo de tiempo considerado. Pero la fuerza multiplicada por el tiempo de la acción es la impulsión; K_tt es el aumento de los componentes de tiempo que tiene la impulsión. Podemos ahora, a capricho, atribuir a un cuerpo en reposo la impulsión temporal J⁰_t = M₀; en tal caso, habrá que poner K_tt = J_t - J⁰_t = J_t - m₀, y se obtiene

$J_{t}={\frac {T}{c^{2}}}+m_{0}=m$.[83]

Esta es una nueva forma de la ley de la energía; según ella, el componente temporal de la impulsión es igual a la masa (relativista) del cuerpo. Pero la masa misma difiere de su valor en reposo justamente en la misma cantidad que el valor de la energía cinética partido por el cuadrado de la velocidad de la luz.

Esto sugiere la idea de que la masa en reposo M₀ (que, según la definición que acabamos de dar, es igual al componente temporal de la impulsión en reposo) está en relación de la misma manera con el contenido de energía del cuerpo en reposo y que, por tanto, entre toda masa y energía existe la relación universal:

$m={\frac {E}{c^{2}}}$.

Einstein ha caracterizado esta ley de la inercia de la energía como el más importante resultado de la teoría de la relatividad; en efecto, significa la identidad de los dos conceptos fundamentales de masa y energía y abre así profundísimas perspectivas en la estructura de la materia. Antes de hablar de ello, comunicaremos la sencilla demostración de la fórmula [84] que Einstein da.

Apóyase en el hecho de que existe la presión radiante. De las ecuaciones de Maxwell, con la ayuda de una ley deducida por Poynting (1884), se sigue que una onda luminosa que penetra en un cuerpo absorbente ejerce sobre éste una presión; y se manifiesta que la impulsión que ejerce sobre la superficie absorbente un corto relámpago o choque de luz es igual a ${\tfrac {E}{c}}$. Este resultado ha sido confirmado experimentalmente por Lebedew (1890) y más tarde también por Nichols y Hull (1901) con mayor exactitud. Un cuerpo que envía luz experimenta exactamente la misma presión, lo mismo que un disparo de arma de fuego produce un retroceso.

fig121

Imaginemos ahora un cuerpo hueco, por ejemplo, un tubo largo, y en las extremidades de éste dos cuerpos, A y B, de igual tamaño, del mismo material, los cuales, por tanto, tienen la misma masa, según las representaciones corrientes (fig. 121). Pero el cuerpo A tiene un exceso de energía E sobre B, por ejemplo, en forma de calor, y se arregla un dispositivo (espejo cóncavo o cosa por el estilo) para enviar esa energía E a B en forma de radiación. Supongamos también que la extensión espacial de ese rayo de luz sea pequeña relativamente a la longitud l del tubo.

A experimenta el choque de retroceso ${\tfrac {E}{c}}$; por tanto, el tubo entero, cuya masa total es M, recibe una velocidad v dirigida hacia atrás, que se determina por la ecuación de impulsión

$Mv={\frac {E}{c}}$.

Este movimiento dura hasta que el rayo de luz llega a B y es allí absorbido; B entonces sufre el mismo choque hacia adelante, y todo el sistema entra, pues, en reposo. El desplazamiento que ha sufrido durante el tiempo t que ha tardado el rayo en recorrer el tubo es x = vt, siendo v derivable de la anterior ecuación; es, por lo tanto,

$x={\frac {Et}{Mc}}$.

Pero el tiempo del recorrido es (hasta un pequeño error de orden elevado) determinado por l = ct; el desplazamiento es, pues:

$x={\frac {El}{Mc^{2}}}$.

Ahora se pueden cambiar los cuerpos A y B uno por otro y ello sin emplear efectos exteriores; figurémonos, por ejemplo, que dos hombres metidos en el tubo ponen A en el lugar de B y B en el de A, y luego vuelven a sus primitivos puestos. Según la mecánica corriente, el tubo no debería experimentar desviación alguna, pues continuas modificaciones de lugar no pueden producirse sino por fuerzas exteriores.

Hecho el cambio, todo quedaría dentro del tubo como estaba al principio: la energía E, en el mismo sitio que antes; la distribución de las masas, igual. Pero todo el tubo sería desplazado relativamente a su posición inicial por el choque de luz a una distancia x. Esto contradice, naturalmente, todos los principios de la mecánica. Podríase repetir el proceso, y así atribuir al sistema, sin emplear fuerzas exteriores, cualquiera modificación de lugar. Esto es imposible. La única salida es admitir que, trocando A por B, estos dos cuerpos no son mecánicamente equivalentes, sino que B, por causa de su exceso E de energía, tiene una masa mayor que A en la cantidad m. Entonces, al hacer el trueque no permanece todo simétrico, sino que la masa m es desplazada de derecha a izquierda a la distancia l. Al ocurrir esto, el tubo entero se desplaza, a una distancia x, en la dirección opuesta; determínase porque el proceso se verifica sin acción de fuerzas exteriores. La impulsión total, que consiste en la del tubo $M{\tfrac {x}{t}}$ y la de la masa transportada $-m{\tfrac {l}{t}}$, es, pues, nula

$Mx-ml=0$;

de donde

$x={\frac {ml}{M}}$

Este desplazamiento debe, pues, compensar al producido por el choque de luz; por tanto, debe ser:

$x={\frac {ml}{M}}={\frac {El}{Mc^{2}}}$.

Por donde cabe calcular m y se halla:

$m={\frac {E}{c^{2}}}$.

Tal es la cantidad de masa inerte que hay que atribuir a la energía E para que siga valiendo el principio de la mecánica que dice que sin acción de fuerzas externas no puede producirse ninguna modificación de lugar.

Como, por último, toda energía puede transformarse en radiación, habrá de tener validez universal la ley. La masa no es, pues, otra cosa que una forma de manifestarse la energía: la materia misma pierde su carácter primario como substancia indestructible; no es más que una concentración de energía. Dondequiera que campos eléctricos y magnéticos u otras acciones conduzcan a fuertes amontonamientos de energía, prodúcese el fenómeno de la inercia de masa. El electrón y los átomos son de esos lugares donde existe una enorme concentración de energía.

De las numerosas e importantes consecuencias de esta ley sólo pueden ocuparnos algunas, y brevemente.

Por lo que se refiere primero a la masa del electrón, demuestra la fórmula [62] (pág. 232) para la masa en reposo $m_{0}={\tfrac {1}{2}}{\tfrac {U}{c^{2}}}$ que la energía electrostática U no puede ser la energía total E del electrón en reposo; tiene que haber además otra parte de energía E = U + V; de suerte que

$m_{0}={\tfrac {4}{3}}{\frac {U}{c^{2}}}={\frac {E}{c^{2}}}={\frac {U+V}{c^{2}}}$.

De aquí se sigue $V={\tfrac {4}{3}}U-U={\tfrac {1}{3}}U={\tfrac {1}{4}}E$; la energía total es, pues, electrostática en sus tres cuartas partes, y de otra clase, en una cuarta parte. Esta parte debe provenir de las fuerzas de cohesión que mantienen el electrón contra la atracción electrostática. Sobre este punto se han desenvuelto muy profundas teorías por Mie, Hilbert y Einstein; sin embargo, los resultados son aún harto poco satisfactorios para poder hablar de ellos aquí. Los más plausibles parecen ser las hipótesis de Einstein, sobre las cuales volveremos brevemente al hablar de la teoría general de la relatividad.

En cambio, para el problema de la estructura de los átomos materiales tiene ya una gran importancia la ley de la inercia de la energía.

Ya hemos dicho antes (pág. 224) que cada átomo consta de una parte positiva inseparablemente unida a la masa inerte y de un número de electrones negativos. Los experimentos de Rutherford (1913) y sus discípulos sobre la dispersión de los rayos positivos emitidos por substancias radioactivas, los llamados rayos α, han demostrado que los elementos positivos de los átomos, que hoy llamamos núcleos, son extraordinariamente pequeños, mucho más pequeños todavía que el electrón, cuyo radio hemos estimado en unos 2 · 10^-13 cm. (pág. 233). Si la masa del núcleo, como la del electrón, fuera en lo esencial (en sus tres cuartas partes) de naturaleza electromagnética, habría de existir entre ella y el radio a una fórmula semejante a la anteriormente aplicada al electrón $m_{0}={\tfrac {2}{3}}{\tfrac {e^{2}}{ac^{2}}}$ (página 232), quizá con un factor numérico algo diferente. Las masas serían, pues, inversamente proporcionales a los radios:

${\frac {\text{radio del electrón}}{\text{radio del núcleo}}}={\frac {\text{masa del núcleo}}{\text{masa del electrón}}}$

Sabemos, empero, que el átomo de hidrógeno es unas 2.000 veces más inerte que el electrón; de aquí se infiere que el radio del núcleo de hidrógeno es unas 2.000 veces más pequeño que el del electrón, en corcondancia con los resultados experimentales.

Puede, pues, aplicarse con éxito a las masas de los átomos o núcleos la ley de la inercia de la energía.

Los átomos radioactivos emiten, como es sabido, tres especies de rayos: 1.°, rayos α, que son partículas cargadas positivamente, que se han manifestado como núcleos de helio; 2.°, rayos β, que son electrones; 3.°, rayos γ, que son ondas electromagnéticas de la naturaleza de los rayos Röntgen. Al emitir estos rayos, pierde el átomo, no sólo masa, sino además energía en cantidad notable; pero si pierde energía, tendrá que disminuir también la masa, según la ley de la inercia de la energía. Desgraciadamente, es tan pequeña esa diminución de masa, que hasta ahora no ha sido posible determinarla experimentalmente.

Pero, en principio, tiene altísima significación el conocimiento de que, al deshacerse un átomo, las masas de sus elementos sumadas no son iguales a la masa del átomo primitivo. Es un viejo objetivo de la investigación el reducir todos los átomos a más simples elementos. Prout (1815) ha establecido la hipótesis de que esos elementos originarios son los átomos de hidrógeno; fundamenta su idea señalando el hecho de que los pesos de muchos átomos son múltiplos enteros del peso del átomo de hidrógeno. La exacta medición de los pesos atómicos no ha confirmado tal aserto, por lo cual la hipótesis de Prout cayó en descrédito. Pero hoy ha sido restaurada con éxito, pues, según la ley de la inercia de la energía, la masa de un núcleo atómico, formado de n núcleos de hidrógeno, no será simplemente igual a n veces la masa del núcleo de hidrógeno, sino que será distinta, en un valor igual a la cantidad de energía transformada al verificarse la reunión. Recientemente esta concepción ha encontrado un fuerte apoyo en el descubrimiento, hecho por Rutherford (1919), de que bombardeando átomos de nitrógeno con rayos x pueden desprenderse de aquéllos núcleos de hidrógeno. Sin duda la ley de la inercia de la energía no puede explicar las relaciones entre un peso atómico y el peso del átomo de hidrógeno más que cuando se aparten poco del número entero; pero existe además otra causa que produce las grandes diferencias, el hecho de la isotopía. Muchos elementos son mezclas de átomos con núcleos igualmente cargados e igual ordenación de los electrones; pero distintas masas nucleares; éstos no pueden separarse químicamente, pero si físicamente. La existencia de isótopos fué probada primeramente en substancias radioactivas, y recientemente Aston (1920) los ha encontrado en muchos otros elementos. Sin embargo, no podemos detenernos en este interesante tema.

Esta rápida ojeada en los problemas de la moderna atomística demuestra que la teoría de la relatividad de Einstein no es el parto de una especulación fantástica, sino un profundo guía en las esferas más importantes de la investigación física. Rasgar el velo que encubre aún el mundo de los átomos es, para la evolución espiritual de la humanidad, un objetivo que supera en grandiosidad y en trascendencia todos los demás problemas de la ciencia natural; acaso incluso el conocimiento de la estructura del universo. Pues todo progreso por ese camino no sólo nos da nuevas armas para la lucha por la vida, sino conocimientos de las más hondas conexiones que tejen el universo natural y nos enseña a distinguir entre el engaño de los sentidos y la verdad de las eternas leyes del Todo.

9. Optica de los cuerpos en movimiento.

Habiendo ya sacado las más importantes consecuencias de la mecánica nueva, es tiempo de volver a aquellos problemas de donde nació la teoría de la relatividad de Einstein, la electrodinámica y la óptica de los cuerpos en movimiento. Las leyes fundamentales de esas esferas están en las ecuaciones de Maxwell resumidas, y ya Lorentz había conocido que, para el espacio vacío (ε = 1, μ = 1 σ = 0), eran invariantes en las transformaciones de Lorentz. Las exactas ecuaciones invariantes para cuerpos en movimiento han sido establecidas por Minkowski (1907); distínguense de las fórmulas dadas por Lorentz en la teoría electrónica, sólo por algunos miembros accesorios, que no pueden comprobarse por observación, pero tienen de común con ellas el arrastre parcial de la polarización dieléctrica, y explican, por tanto, todos los procesos electromagnéticos y ópticos en cuerpos en movimiento, con plena concordancia con las observaciones; recordemos especialmente los experimentos de Róntgen, Eichenwald y Wilson (V, 11, página 212); pero no podemos insistir sobre este punto porque son necesarias en él deducciones matemáticas detalladas. La óptica de los cuerpos en movimiento puede, empero, ser tratada elementalmente, y vamos a exponerla aquí como una de las más hermosas aplicaciones de la teoría de Einstein.

En ésta no hay éter, sino sólo cuerpos que se mueven relativamente unos a otros. Evidente resulta, según la teoría de la relatividad de Einstein, que todos los procesos ópticos, en los cuales los focos luminosos, las substancias transparentes y el observador están en uno y el mismo sistema inercial, son los mismos para todos los sistemas inerciales. La teoría de la relatividad explica, pues, también el experimento de Michelson, que es de donde ha nacido. Sólo se trata, pues, aquí de saber si la teoría reproducirá exactamente los fenómenos que se verifiquen hallándose en movimiento relativo el foco luminoso, el medio transparente y el observador.

Imaginemos una onda luminosa en un cuerpo material que se halla en reposo en el sistema de referencia S; sea su velocidad $c_{1}={\tfrac {c}{n}}$ (n es el índice de refracción); sea su número de vibraciones ν, y esté dada su dirección relativamente al sistema S.

Queremos saber cómo esos tres caracteres de la onda son juzgados por un observador que se halla en reposo en un sistema de referencia S', el cual se mueve con la velocidad v paralelamente a la dirección x del sistema S.

Trataremos este problema según el mismo método que le hemos aplicado antes (IV, 7, pág. 136), sólo que, en vez de emplear las transformaciones de Galileo, emplearemos las de Lorentz. Ya hemos demostrado allí que el número de ondas

$\nu \left(t-{\frac {s}{c}}\right)$

es una invariante, pues significa las ondas que a partir del momento t = 0 salen del punto cero y hasta el momento t llegan al punto P, recorriendo la distancia s (fig. 67, pág. 138). Esta invariancia rige naturalmente ahora también para transformaciones de Lorentz.

Consideremos primeramente ondas que se propagan paralelas a la dirección x; en tal caso habrá que poner para s la coordenada x del punto P, y tendremos:

$\nu \left(t-{\frac {x}{c_{1}}}\right)=\nu '\left(t-{\frac {x'}{c'_{1}}}\right)$,

donde ν, ν' y c₁, c'₁ son las frecuencias y velocidades de la onda relativamente a los sistemas S y S'. Si en la derecha se ponen las expresiones que para x' y t' nos da la transformación de Lorentz [65] (pág. 261), tendremos:

$\nu \left(t-{\frac {x}{c_{1}}}\right)={\frac {\nu '}{\alpha }}\left(t-{\frac {v}{c^{2}}}x-{\frac {x-vt}{c'_{1}}}\right)$;

donde $\alpha ={\sqrt {1-\beta ^{2}}}={\sqrt {1-{\tfrac {v^{2}}{c^{2}}}}}$. Si se pone primero x = 1, t = 0 y luego t = 1, x = 0, se obtiene:

${\begin{cases}{\frac {\nu }{c_{1}}}&={\frac {\nu '}{\alpha }}\left({\frac {v}{c^{2}}}+{\frac {1}{c'_{1}}}\right),\\\nu &={\frac {\nu '}{\alpha }}\left(1+{\frac {v}{c'_{1}}}\right).\end{cases}}$[85]

Si se divide la primera ecuación por la segunda, obtiénese:

$c_{1}={\frac {1+{\frac {v}{c'_{1}}}}{{\frac {v}{c^{2}}}+{\frac {1}{c'_{1}}}}}={\frac {c'_{1}+v}{1+{\frac {vc'_{1}}{c^{2}}}}}$.

Si se resuelve a la inversa buscando el valor de c'₁, se obtiene la fórmula estricta de arrastre:

$c'_{1}={\frac {c_{1}-v}{1-{\frac {vc_{1}}{c^{2}}}}}$.

Esta concuerda exactamente con el teorema de la adición de las velocidades, de Einstein, en movimiento longitudinal (primera fórmula [70], pág. 287), si se substituye u_p por c₁ y u'_´p por c'₁. La misma regla que vale para calcular las velocidades de los cuerpos materiales, relativamente a diferentes sistemas de referencia, vale, pues, también para la velocidad de la luz.

Mas esta ley es idéntica a la fórmula de arrastre dada por Fresnel [39] (pág. 156), si se desprecian miembros de más del segundo orden en $\beta ={\tfrac {v}{c}}$. Pues con esa aproximación puede escribirse

${\frac {1}{1-{\frac {vc_{1}}{c^{2}}}}}={\frac {1}{1-{\frac {\beta }{n}}}}=1+{\frac {\beta }{n}}=1+{\frac {v}{nc}}$;

esto es:

${\begin{aligned}c'_{1}&=(c_{1}-v)\left(1+{\frac {v}{nc}}\right)\\&=c_{1}-v+{\frac {vc_{1}}{nc}}-{\frac {v^{2}}{nc}}\end{aligned}}$,

y prescindiendo otra vez del miembro último, que es del segundo orden, y poniendo ${\tfrac {c_{1}}{c}}={\tfrac {1}{n}}$:

$c'_{1}=c_{1}-v\left(1-{\frac {1}{n^{2}}}\right)$.

Y ésta es exactamente la fórmula de arrastre de Fresnel.

La segunda de las fórmulas [85] representa el principio de Doppler; éste se aplica comúnmente al vacío, poniendo, pues, c₁ = c, y entonces del teorema de la adición de las velocidades se sigue, como es sabido (pág. 287), también que c'₁ = c. La segunda de las fórmulas [85] resulta, pues:

$\nu '=\nu {\frac {\alpha }{1+{\frac {v}{c}}}}=\nu {\frac {\sqrt {1-\beta ^{2}}}{1+\beta }}$;

pero 1 - β² = (1 - β)(1 + β); por lo cual puede escribirse:

$\nu '=\nu {\frac {\sqrt {(1-\beta )(1+\beta )}}{1+\beta }}=\nu {\sqrt {\frac {1-\beta }{1+\beta }}}$,

La fórmula estricta del efecto de Doppler recibe así la forma simétrica siguiente:

$\nu '={\sqrt {1+{\frac {v}{c}}}}=\nu {\sqrt {1-{\frac {v}{c}}}}$,

que pone en evidencia la equivalencia de los sistemas de referencia S y S'. Si ahora despreciamos los miembros de más del orden segundo, podemos substituir ${\sqrt {1+\beta }}$ por $1+{\tfrac {1}{2}}\beta$ y ${\sqrt {1-\beta }}$ por $1-{\tfrac {1}{2}}\beta$; obtiénese, pues:

${\begin{aligned}\nu '\left(1+{\tfrac {1}{2}}\beta \right)&=\nu \left(1-{\tfrac {1}{2}}\beta \right)\\\nu '&=\nu {\frac {1-{\tfrac {1}{2}}\beta }{1+{\tfrac {1}{2}}\beta }};\end{aligned}}$

ahora bien, con igual exactitud es

${\frac {1}{1+{\tfrac {1}{2}}\beta }}=1-{\tfrac {1}{2}}\beta$,

por lo cual

$\nu '=\nu \left(1-{\tfrac {1}{2}}\beta \right)^{2}=\nu \left(1-\beta +{\tfrac {1}{2}}\beta ^{2}\right)$,

y, despreciando β²:

$\nu '=\nu \left(1-{\frac {v}{c}}\right)$,

en completa concordancia con la fórmula [36] (pág. 143).

Para deducir por el mismo método la aberración de la luz, debemos considerar un tren de ondas que se propaga perpendicularmente a la dirección x del movimiento de los sistemas S y S' uno con respecto del otro; pero debemos añadir si la dirección perpendicular se refiere a S o a S' pues si el rayo es perpendicular al eje x relativamente a S no lo es relativamente a S'. Vamos a admitir que la dirección de propagación es el eje y' del sistema S'; en tal caso hay que poner s' = y' y para el vacío regirá (c₁ = c'₁ = c):

$\nu \left(t-{\frac {s}{c}}\right)=\nu '\left(t'-{\frac {y'}{c}}\right)$,

Si se ponen aquí los valores dados por la transformación de Lorentz [65] (pág. 261) se obtiene:

$\nu \left(t-{\frac {s}{c}}\right)=\nu '\left({\frac {t-{\frac {v}{c^{2}}}x}{\alpha }}-{\frac {y}{c}}\right)$;

de aquí se sigue primero, para x = 0, y = 0, s = 0 y t = 1,

$\nu ={\frac {\nu '}{\alpha }}$;

y después, para t = 0:

${\frac {\nu }{c}}s=\nu '\left({\frac {vx}{c^{2}\alpha }}+{\frac {y}{c}}\right)={\frac {\nu '}{\alpha c}}(\beta x+\alpha y)$,

esto es:

$s=\alpha y=\beta x$.

fig122

Si el plano de onda relativamente al sistema de referencia S fuese perpendicular al eje y, tendríamos s = y; como éste no es el caso, deberá estar inclinado (fig. 122). Entonces x ó y son las coordenadas de un punto P del plano de onda. Si elegimos para P especialmente la intersección A con el eje x, será x = a, y = 0 y, por tanto, s = βa; igualmente para la intersección β del plano de onda con el eje y, es x = 0, y = b y, por tanto, s = xb.

Se obtiene así:

$s=\beta a=\alpha b\$ ó $\ {\frac {b}{a}}={\frac {\beta }{\alpha }}$

Esta relación ${\tfrac {b}{a}}$ es, evidentemente, una medida para la inclinación del frente de onda. Se ve fácilmente que coincide con la definición elemental de la constante de aberración según la teoría de la emisión (IV, 3, pág. 109). Pues la perpendicular OC, trazada por el punto cero en el plano de onda, es la dirección de propagación; si D es la proyección de C sobre el eje x, será OD = d, la desviación que hay que dar a un telescopio paralelo al eje y y de longitud DC = l, durante el tiempo que la luz necesita para recorrer el tubo, para que un rayo de luz que toque en C el centro del objetivo alcance justamente en O el centro del ocular. Es, pues, ${\tfrac {d}{l}}$ la constante de aberración. Por la semejanza de los triángulos OCD y BOA, resulta la proporción:

${\frac {d}{l}}={\frac {b}{a}}={\frac {\beta }{\alpha }}={\frac {\beta }{\sqrt {1-\beta ^{2}}}}$.

Esta es la fórmula exacta de la aberración. Si se desprecia β². comparado con 1, transfórmase en la fórmula elemental

${\frac {d}{l}}=\beta ={\frac {v}{c}}$

Este resultado es particularmente notable, porque todas las teorías del éter habían de resolver considerables dificultades al explicar la aberración. Empleando la transformación de Galileo, no se obtiene ninguna inclinación del plano de onda y de la dirección de las ondas (IV, 10, pág. 159), y para explicar la aberración hay que introducir entonces el concepto de «rayo», que no necesita concordar con la dirección de propagación en los sistemas en movimiento. En la teoría de Einstein no es ello necesario; en todo sistema inercial S, la dirección del rayo, es decir, del transporte de energía, coincide con la perpendicular sobre el plano de onda, y, sin embargo, resulta la aberración, en la misma sencilla manera que el efecto de Doppler y el número de arrastre de Fresnel, con sólo deducirla del concepto de onda, por medio de la transformación de Lorentz.

Esta deducción de las leyes fundamentales de la óptica de los cuerpos en movimiento demuestra la superioridad de la teoría de la relatividad frente a todas las demás teorías.

10. El universo absoluto de Minkowski.

fig123

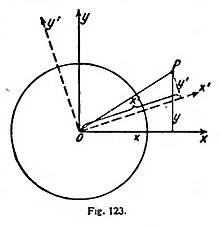
La esencia de la nueva cinemática consiste en la unión inseparable del espacio con el tiempo. El universo es una multiplicidad de cuatro dimensiones; su elemento es el punto universal; el espacio y el tiempo son formas de la ordenación de los puntos universales y esa ordenación es, hasta cierto punto, empañada de contingencia. Minkowski ha resumido esta concepción en las palabras: «de aquí en adelante el espacio y el tiempo por sí deben tornarse sombras y sólo conserva independencia una especie de unión de ambos conceptos». Y ha desarrollado consecuentemente esta idea, desenvolviendo la cinemática como una geometría de cuatro dimensiones. Nosotros hemos hecho uso continuamente de su exposición, prescindiendo solamente de los ejes y y z, para simplificar, y operando en el plano xt. Si desde el punto de vista matemático lanzamos una mirada a la geometría en el plano xt reconoceremos al punto que no se trata de la geometría euclidiana corriente. Pues en esta última todas las rectas que parten del punto cero son igualmente legitimas, la unidad de longitud en todas ellas es la misma; la curva estimativa es, pues, un círculo (fig. 123). Pero en el plano xt no son de igual valor las rectas de tiempo y las rectas de espacio; en cada una rige una unidad diferente de longitud, y la curva estimativa consta de las hipérbolas:

$G=x^{2}-c^{2}t^{2}=\pm 1$.

En el plano euclidiano pueden construirse sistemas de coordenadas rectangulares en número infinito, todos con el mismo punto cero, y todos salen unos de otros por rotación. En el plano xt hay igualmente un número infinito de sistemas de coordenadas igualmente válidos, en los cuales uno de los ejes puede ser elegido a capricho dentro de un cierto ángulo.

En la geometría euclidiana la distancia s de un punto P al punto cero queda expresada por las coordenadas x é y, según el teorema de Pitágoras, por la fórmula siguiente (fig. 123):

$s^{2}=x^{2}+y^{2}$;

y esta expresión es invariante frente a una rotación del sistema de coordenadas, es decir, que para un sistema x'y' será s² = x'² + y'². La curva estimativa es representada por s = 1.

En el plano xt, la invariante fundamental es:

$G=x^{2}-c^{2}t^{2}$.

y la curva es

$G=\pm 1$.

Minkowski ha observado que aquí se manifiesta un paralelismo que da mucha luz acerca de la estructura matemática del universo cuatridimensional (y, por tanto, del plano xt). En efecto, si se pone -c²t² = u², tendremos:

$G=x^{2}+u^{2}=s^{2}$

y entonces G puede concebirse como invariante fundamental s² de una geometría euclidiana con coordenadas rectangulares x, u.

Sin duda, no es posible sacar la raíz cuadrada de la cantidad negativa -c²t² y u mismo no puede calcularse por el tiempo t. Pero la matemática está habituada desde hace mucho tiempo a vencer con audacia tales dificultades. La cantidad «imaginaria» ${\sqrt {-1}}=i$ tiene, desde Gauss, derecho de ciudadanía en el Estado matemático. No podemos ocuparnos aquí de la estricta fundamentación de la teoría de los números imaginarios; en el fondo no son ni más ni menos «imaginarios» que un quebrado, como ⅔. En efecto, los números «con que se calcula» son propiamente sólo los números naturales, los enteros 1, 2, 3, 4..... El número 2 no puede dividirse por 3, y ⅔ es una operación tan irrealizable como ${\sqrt {-1}}$. Los quebrados como ⅔ significan una amplificación del concepto natural de número, que la escuela y la costumbre han hecho corriente y fácil de entender. Una amplificación semejante del concepto de número son los números imaginarios, que para los matemáticos son tan habituales y corrientes como los cálculos de quebrados. Todas las fórmulas que contienen números imaginarios poseen una significación tan precisa como las que están formadas de números «reales» habituales; y las consecuencias que de ellas salgan son igualmente necesarias.

Si, pues, empleamos aquí el símbolo ${\sqrt {-1}}=i$, podemos escribir:

$u=ict$

La geometría no euclidiana del plano xt es, pues, formalmente idéntica a la geometría euclidiana en el plano xu, con la única diferencia de que a los tiempos reales t corresponden valores imaginarios u.

Este aserto es de inapreciable valía para el tratamiento matemático de la teoría de la relatividad. Pues en muchísimas operaciones y cálculos no importa la realidad de las cantidades consideradas, sino sólo las relaciones algebraicas que existen entre ellas, las cuales rigen igual para números imaginarios que para números reales. Pueden, pues, trasladarse al universo cuatridimensional las leyes conocidas de la geometría euclidiana. Minkowski substituye

$x\quad y\quad z\quad ict$

por

$x\quad y\quad z\quad u$

y opera luego con estas cuatro coordenadas en manera totalmente simétrica. La invariante fundamental es entonces:

$G=s^{2}=x^{2}+y^{2}+z^{2}+u^{2}$

La posición peculiar del tiempo desaparece así de todas las fórmulas, lo cual aumenta mucho la comodidad y claridad de los cálculos. En el resultado final hay que volver a poner ict en lugar de u, no conservando sentido físico sino aquellas ecuaciones que están formadas exclusivamente con números reales.

El que no sea matemático no podrá pensar gran cosa bajo estas consideraciones; acaso indignado ante la que Minkowski mismo llama, medio en broma, «ecuación mística» $3\cdot 10^{10}{\text{ cm.}}={\sqrt {-1}}{\text{ sec.}}$, se ponga del lado de los críticos que atacan la teoría de la relatividad, por parecerles puro absurdo el equiparar el tiempo a las dimensiones del espacio.

Esperamos, sin embargo, que nuestro método de exposición, en el cual el método formal de Minkowski sólo aparece al final, podrá resistir a tales ataques. En el plano xt, el tiempo t no puede de ninguna manera confundirse con la dimensión de longitud x; las líneas luminosas ξ y η, separan, cual barreras infranqueables, las líneas universales de tiempo de las líneas universales de espacio. La transformación de Minkowski u = ict debe, pues, apreciarse como un artificio matemático que destaca en verdadera luz ciertas analogías formales entre las coordenadas de espacio y el tiempo, sin admitir por ello una confusión entre ellas.

Pero de ese artificio han resultado importantes conocimientos. Sólo citaremos la nueva concepción de la ley de la energía, que en la exposición de Minkowski se manifiesta junto a la ley de la impulsión, como relación equivalente y de igual fórmula entre los componentes temporales. Podemos inferirlo de la fórmula [83] de la ley de la energía. Para ello formaremos los componentes temporales de la velocidad $v_{t}={\tfrac {t}{t}}=1$, por modo análogo a los componentes x de la velocidad $v={\tfrac {x}{t}}$, y en la fórmula [83] los incluiremos. Entonces obtendremos la ley de la energía en la forma J_t = mv_t, que se formula igual que la de la impulsión espacial J = mv. Si se parte del principio de Minkowski de que hay una analogía entre el tiempo y las coordenadas, obtiénese entonces la recta visión en las conexiones interiores de todas estas relaciones.

Ante todo, sin ese artificio matemático, la teoría de la relatividad de Einstein sería impensable. Importa en esto la analogía de la invariante fundamental G con el cuadrado de una distancia. En lo futuro, para la magnitud:

$s={\sqrt {G}}={\sqrt {x^{2}+y^{2}+z^{2}+u^{2}}}={\sqrt {x^{2}+y^{2}+z^{2}-c^{2}t^{2}}}$[86]

emplearemos la designación de distancia cuatridimensional, habiendo de conservar clara conciencia de que esa palabra se entiende en sentido traslaticio.

El sentido propio de la magnitud s es, según nuestras explicaciones anteriores sobre la invariante G, fácil de comprender. Si nos limitamos al plano xt, será:

$s={\sqrt {G}}={\sqrt {x^{2}+u^{2}}}={\sqrt {x^{2}-c^{2}t^{2}}}$.

Ahora bien; G es positivo para toda línea universal de espacio; por tanto, s, como raíz cuadrada de un número positivo, es una cantidad real; entonces el punto universal x, t, si se elige un sistema conveniente de referencia, puede hacerse simultáneo con el punto cero. En tal caso es t = 0 y $s={\sqrt {x^{2}}}=x$, esto es, la distancia espacial entre el punto cero y el punto universal.

Para toda línea universal de tiempo, G es negativo y, por tanto, s imaginario; entonces hay un sistema de coordenadas, en el cual x = 0 y $s={\sqrt {-c^{2}t^{2}}}=ict$. En todo caso tiene s una significación sencilla y debe considerarse como magnitud mensurable.

Terminamos con esto la exposición de la teoría especial de la relatividad de Einstein. Su resultado podemos resumirlo del modo siguiente:

No sólo las leyes de la mecánica, sino las de todos los procesos naturales, y particularmente los fenómenos electromagnéticos, son perfectamente idénticas, en sistemas de referencia infinitamente numerosos, que se hallen en movimiento uniforme de traslación relativamente unos a otros; estos sistemas se llaman inerciales. En cada uno de estos sistemas rige una especial medida para longitudes y tiempos, y estas medidas hállanse relacionadas entre sí por medio de las transformaciones de Lorentz.

Otros sistemas de referencia que se muevan con movimiento acelerado relativamente a los sistemas inerciales no son equivalentes a los sistemas inerciales, exactamente como sucede en la mecánica. Si las leyes de la naturaleza se refieren a esos sistemas acelerados, tendrán fórmulas distintas; en la mecánica manifiéstanse fuerzas centrífugas y en la electrodinámica acciones análogas, cuyo estudio nos llevaría demasiado lejos. La teoría especial de la relatividad de Einstein no suprime, pues, el espacio absoluto de Newton en el sentido limitado que hemos dado antes a esta palabra (III, 6, pág. 84); lo que hace es establecer para toda la física, incluida la electrodinámica, la situación misma en que se hallaba la mecánica desde Newton. Los profundos problemas del espacio absoluto, que en esta mecánica nos preocuparon, siguen, pues, sin solución; no hemos dado apenas un paso en el sentido de esta solución; es más, la amplificación del objeto físico allende los limites de la mecánica ha aumentado esencialmente la dificultad del problema.

Ahora vamos a ver cómo Einstein ha podido resolverlo.

---

1. No podemos entrar aquí en la diferencia de vectores covariantes y contravariantes.
2. Es, efectivamente, $${\frac {v+w_{p}}{\sqrt {1-\left({\frac {v+w_{p}}{c}}\right)^{2}}}}={\frac {v+w_{p}}{\sqrt {1-{\frac {1}{c^{2}}}(v^{2}+2vw_{p}+w_{p}^{2})}}}$$ o sea, despreciando w²: $$\qquad \qquad \qquad \quad ={\frac {v+w_{p}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}-2{\frac {vw_{p}}{c^{2}}}}}}$$ Si se hace uso a hora de la abreviación antes usada (VI, 2, fórmula [64], pagina 261) $\alpha ={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$, la expresión se transforma en
   ${\frac {v+w_{p}}{\alpha {\sqrt {1-{\frac {2vw_{p}}{\alpha ^{2}c^{2}}}}}}}$

   Y si empleamos la fórmula de aproximación

   ${\frac {1}{\sqrt {1-x}}}=1+{\frac {1}{2}}x$

   anteriormente deducida (nota a la pág. 237), obtenemos, despreciando w²_p

   ${\frac {v+w_{p}}{\alpha }}\left(1+{\frac {vw_{p}}{\alpha ^{2}c^{2}}}\right)={\frac {1}{\alpha }}\left\{v+w_{p}\left(1+{\frac {v^{2}}{\alpha ^{2}c^{2}}}\right)\right\}={\frac {1}{\alpha }}\left\{v+{\frac {w_{p}}{\alpha }}\right\}$

   de donde, finalmente,

   ${\frac {v+w_{p}}{\sqrt {1-\left({\frac {v+w_{p}}{c}}\right)^{2}}}}-{\frac {v}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\alpha }}\left\{v+{\frac {w_{p}}{\alpha ^{2}}}\right\}-{\frac {v}{\alpha }}={\frac {w_{p}}{\alpha ^{2}}},$

   que coincide con la fórmula del texto para la modificación longitudinal de la impulsión arrastrada J.

   En la deducción de la fórmula para la modificación transversal de la impulsión no hay mas que reflexionar en que ésta al principio no tiene ningún componente transversal y que la modificación de v en el denominador puede despreciarse porque sólo daría un miembro del segundo orden.

3. En efecto, si se aumenta v en la cantidad w_p, tendremos
   ${\begin{aligned}{\frac {1}{\sqrt {1-\left({\frac {v+w_{p}}{c}}\right)^{2}}}}&={\frac {1}{\sqrt {1-{\frac {1}{c^{2}}}(v^{2}+2vw_{p}+w_{p}^{2})}}}\\{\text{y aproximadamente }}&={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}-{\frac {2vw_{p}}{c^{2}}}}}}={\frac {1}{\alpha {\sqrt {1-{\frac {2vw_{p}}{\alpha ^{2}c^{2}}}}}}}\\{\text{aproximadamente }}&={\frac {1}{\alpha }}\left(1+{\frac {vw_{p}}{\alpha ^{2}c^{2}}}\right).\end{aligned}}$

   Esto es:

   ${\frac {1}{\sqrt {1-\left({\frac {v+w_{p}}{c}}\right)^{2}}}}-{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\alpha }}\left(1+{\frac {vw_{p}}{\alpha ^{2}c^{2}}}\right)-{\frac {1}{\alpha }}={\frac {vw_{p}}{\alpha ^{2}c^{2}}},$

   y de aquí se sigue en seguida la fórmula del texto.