Principio de relatividad/II
CAPÍTULO II
9.
Lo dicho en el capítulo precedente muestra que en el grupo de Galileo, como traducción del principio de relatividad, van implícitamente contenidas nociones cuya evidencia dista mucho de ser inmediata, de modo que su empleo equivale a agregar dos nuevos postulados a los que formuló Newton: el de indeformabilidad de los cuerpos por efecto del movimiento, que equivale a atribuir a la Geometría de Euclides el carácter de ciencia natural, y el de independencia de las nociones de tiempo y espacio. Quizá una forma más precisa para este último postulado sea la siguiente: en dos sistemas cuyo movimiento relativo es rectilíneo y uniforme, los únicos fenómenos que se propagan con idéntica velocidad, c en ambos, son aquellos para los cuales .
Pero la introducción más o menos consciente de estos postulados no ha impedido que, mediante el grupo referido, se haya elaborado todo el maravilloso edificio de la Mecánica de Newton, gracias a la cual se formularon leyes precisas para fenómenos tan importantes como el movimiento de los cuerpos que integran nuestro sistema planetario. Si al repasar las páginas destinadas en cualquier tratado de Mecánica a esta teoría se piensa en el caos de la Astronomía anterior a Newton, se comprende que el grandioso éxito logrado haya hecho olvidar a muchas generaciones la necesidad de analizar con cierto cuidado los principios fundamentales de esta ciencia, y aun se la haya elevado a un rango en la clasificación de nuestros conocimientos que su propio autor distaba mucho de atribuirle.
Cierto que muchas particularidades de los movimientos planetarios escaparon en un principio a su interpretación; pero casi todos estos problemas fueron resolviéndose a medida que se perfeccionaba el conocimiento del sistema solar, y aun en ocasiones fué camino para el descubrimiento de nuevos planetas, como en el caso de Neptuno. Por eso los pocos enigmas que iban quedando, siquiera fuesen tan importantes como la rotación secular del eje mayor de la órbita de Mercurio, no se creía que bastasen para motivar la alteración en sus mismos cimientos de la obra de NewtOn. Y no es que la crítica haya dejado de laborar sobre el valor de los postulados de la Mecánica, sino que realmente penetró poco en su contenido, y dejó intacto cuanto en ella es verdaderamente fundamental.
No sólo se tradujo la admiración debida a la obra de Newton por este respeto hacia ella, sino también por el deseo de utilizarla como base para la interpretación de los fenómenos naturales que no son simples movimientos aparentes de los cuerpos, bien considerándoles como manifestaciones sensibles de mecanismos ocultos, según procuran hacerlo las teorías atómicas, bien abordando el estudio de la Física mediante una generalización de los principios fundamentales de la Mecánica y la imitación de sus métodos de razonar. Este fué el camino seguido en todo el pasado siglo, y del acierto de su elección, por lo menos para un primer desbroce, es clara prueba el maravilloso avance de aquella ciencia.
En cambio, desde el punto de vista filosófico resulta que la imposibilidad de determinar el movimiento absoluto queda restringida a la Mecánica: por métodos ópticos y electromagnéticos será posible llegar a conocerlo, todo lo cual supone que el principio de relatividad no afecta a la capacidad de nuestros medios de conocer, sino a un orden particular de procedimientos. Ello es consecuencia de que las ecuaciones fundamentales para los fenómenos electromagnéticos contienen la velocidad, a diferencia de lo que ocurre con la que es base de la Dinámica, en la cual sólo figura la aceleración.
10.
Veamos, en efecto, cuáles son las referidas ecuaciones fundamentales:
a) La primera expresa la relación existente entre las cargas eléctricas y el campo que ellas provocan. La forma más elemental de esta relación es la ley de Coulomb, según la cual
, (10, 1)
donde ε es un factor característico de la naturaleza física del medio material en que los fenómenos se producen (constante dieléctrica); r la distancia del punto en que se determina a la posición ocupada por e, y 4π un factor numérico que responde a las unidades elegidas para las magnitudes eléctricas. Estas unidades imponen también la condición de que en el vacío, y prácticamente en los gases, ε = 1.
La forma de la ley de Coulomb conduce a sustituir la consideración directa de por la de una cierta función que se llama potencial, definida para el caso de una carga e por
, (10, 2) y de la cual notoriamente se deduce que las componentes de serán
Introducir Φ en vez de tiene la ventaja de que al considerar la superposición de los efectos de varias cargas, el campo resultante se ha de calcular aplicando a cada punto la regla del polígono de las fuerzas, mientras el potencial total es una simple suma algébrica. Pero esto no eleva el potencial a la categoría de una verdadera magnitud física, puesto que no es directamente asequible a la experimentación y encierra una constante indeterminada que puse de manifiesto en (10, 2) mediante el término C. En el último capítulo volveré sobre la interpretación física de Φ, entonces veremos que en el momento actual las cosas parecen cambiar de aspecto.
Agregaré aún que cuando las cargas no se hallan localizadas en puntos separados por distancias finitas, sino que éstas son infinitamente pequeñas, y el número de aquéllos muy grande, los razonamientos se simplifican sustituyendo su enumeración completa por una densidad de cargas definida mediante
o sea el límite de la relación de la carga total al volumen en que se encuentra cuando este último tiende hacia cero, de modo que en (10, 1) y (10, 2)será menester reemplazar e por ρdv.
Decía arriba que la ecuación (10, 1) es la forma más elemental de la relación entre el campo y las cargas que lo engendran. Añadiré ahora que de un modo más completo y riguroso esta relación está contenida en la ecuación
(10, 3)
llamada de Poisson, donde ΔΦ es un símbolo que sustituye a
Una u otra ecuación permiten obtener el campo o el potencial cuando se conocen las cargas; pero esta última tiene la ventaja incuestionable de no hacer intervenir más que los valores de ρ y Φ que corresponden a un mismo lugar, mientras por la primera el campo es la consecuencia de la distribución de las cargas en todo el espacio.
b) Cuando una carga se halla en movimiento, el propio campo es transportado por ella, en el sentido de que en los puntos que ocupan en cada instante la misma posición respecto de la carga, tiene idéntico valor y orientación. Si se imaginan dibujadas en el espacio que rodea a la carga curvas que en cada punto son tangentes a , es evidente que todas ellas partirán del lugar ocupado por aquélla, a modo de cabellera, y la misma proposición precedente puede formularse diciendo que la repetida carga lleva consigo el conjunto de sus líneas de fuerza, que así se llaman las curvas en cuestión.
Ahora bien: múltiples experimentos realizados por varios físicos, y primeramente por Rowland, han probado que el indicado movimiento de una carga determina el nacimiento de un campo magnético , definido en magnitud por la expresión
, (10, 4)
donde r es la distancia del lugar ocupado por la carga e al punto donde se determina H, v' la velocidad del movimiento, α el ángulo de esta velocidad con la recta r, y c una constante numéricamente igual a 3×1010 cm./sec., cuyo sentido físico veremos en seguida. Según se ve, el valor de H es constante en todos los puntos de una circunferencia que es normal a la dirección de v' tiene su centro sobre la recta descrita por e. Además, comprueba la experiencia que es tangente a dicha línea; todo ello en la forma que se representa en la fig. 2.
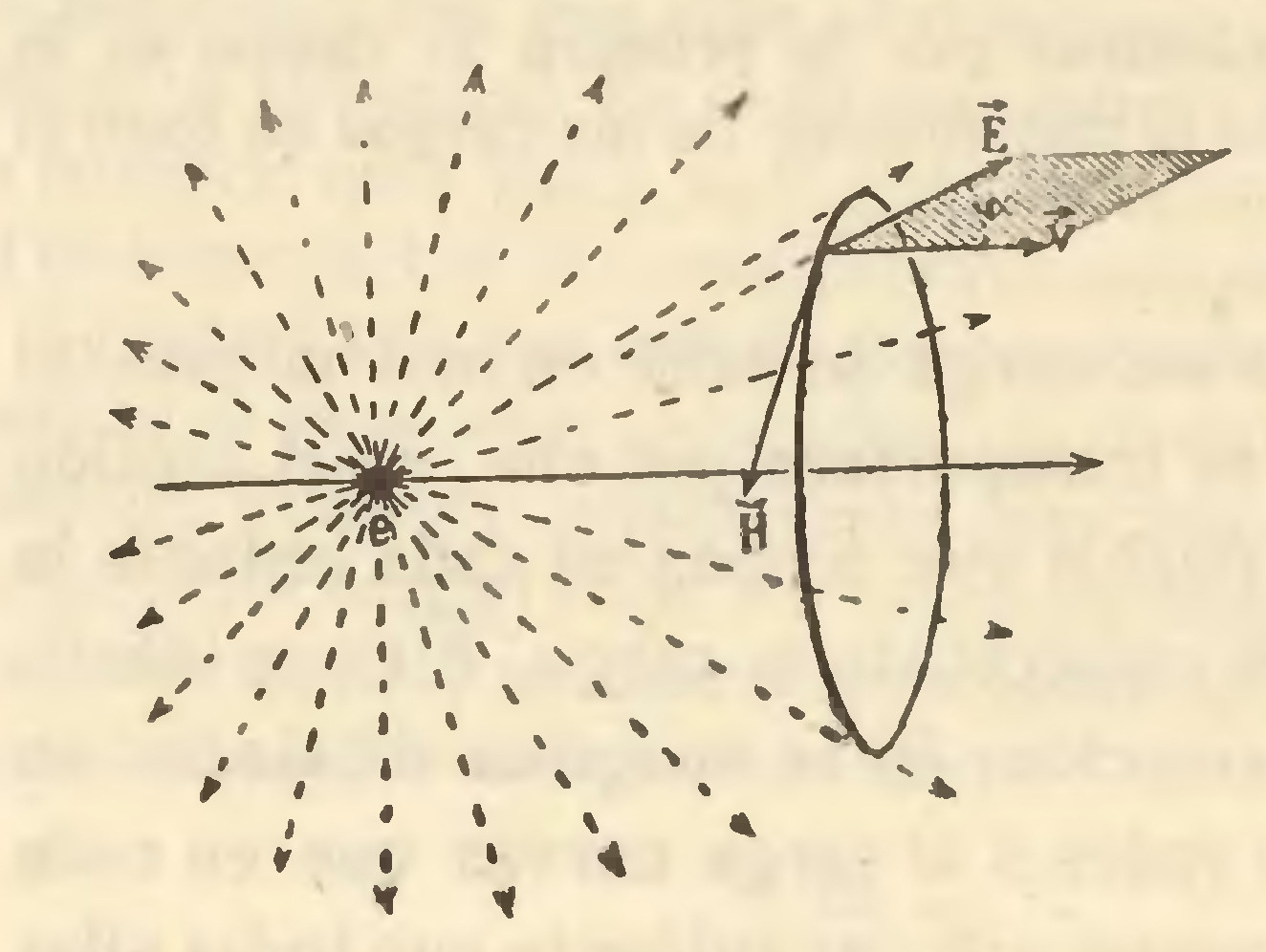
Fig. 2.
Un razonamiento analítico exento de dificultades permite ver que las tres componentes de en un sistema cualquiera de coordenadas cartesianas pueden escribirse en la forma
, , ;
o con una notación general
, (10, 5)
donde las Pj son componentes de un nuevo vector, llamado potencial, que se definen por la ecuación
.(10, 6)
Este vector potencial es, como el escalar Φ, una magnitud cuyo uso simplifica la teoría de estos fenómenos, y paralelamente a lo que con él ocurría, no se halla determinado de modo inequívoco por las cargas y sus velocidades. Aun es aquí mayor la indeterminación que en aquel caso, pues sin dificultad se ve que los valores de Hi no se alteran cuando a cada una de las Pj se agrega la derivada, de una función escalar cualquiera.
Cuando las cargas ocupan un volumen apreciable de modo que sea conveniente reemplazar la consideración de las cargas aisladas por su densidad ρ, en la forma en que he dicho poco más arriba, la simple comparación de las ecuaciones (10, 6) con (10, 2) indica que correspondiendo a (10, 3) debemos escribir
, (10, 7)
mediante la cual se relaciona la corriente ρv' de las cargas con el potencial vector en el mismo lugar.
Volvamos la atención a (10, 4). En ella se puede introducir el campo eléctrico E en vez de , con lo cual
que conduce a interpretar el campo magnético como engendrado en cada lugar por el movimiento del trozo de línea de fuerza que pasa por dicho punto. Como es el área del paralelogramo construído con y como lados, se puede traducir esta fórmula diciendo que la magnitud de es igual a veces el área barrida por E en la unidad de tiempo. Además, su dirección es normal a dicha área, según representa la fig. 2.

Fig. 3
Asi entendido , claro es que sea cual fuere la razón del movimiento de las líneas de fuerza de se engendrará el campo magnético correspondiente. Consideremos un elemento de volumen de un cuerpo donde no haya electrización aparente por existir cargas iguales de signos opuestos superpuestos, según ocurre en estado neutro. Es fácil imaginar una acción que determine el alejamiento de ambas clases de cargas a una distancia d, sustituyendo el elemento de volumen neutro por una pareja. Se demuestra en Electrostática que en el estado de equilibrio permanente existirá un campo cuyas líneas de fuerza se representan en la fig. 3. Pero en nuestro caso dicho estado permanente no se establecerá en todo el espacio instantáneamente, sino que progresivamente irá apareciendo en lugares cada vez más apartados. El proceso se puede describir diciendo que las líneas de fuerza se propagan perpendicularmente a sí mismas y con la velocidad c', que resulta numéricamente igual a la constante c en el vacío, y muy próxima de ella para los medios materiales. Así para este caso
c) Los fenómenos de inducción electromagnética que descubrió Faraday prueban que la producción de un campo magnético por el movimiento de las líneas de fuerza eléctrica tiene su recíproca en la creación de un campo eléctrico en todos los puntos barridos por las líneas de fuerza magnéticas. Este fenómeno se puede comprobar moviendo un imán o un solenoide, que corresponderá al caso en que se mueven las cargas eléctricas, o estableciendo una corriente en una bobina, que será lo análogo a la creación de la pareja a que me referí antes. En el primer caso la ley que define se puede representar, en cuanto a su magnitud, mediante
, (10, 9)
donde μ es una constante específica del medio, como antes lo era ε, mientras v'' es la velocidad del sistema que es origen de y β el ángulo que forman entre si y . Conviene, además, advertir que la posición de respecto de y , es precisamente la opuesta de la de respecto a y en el caso antericr.
En el segundo caso el movimiento de las líneas de fuerza magnéticas se produce también con la velocidad c' y normalmente a ellas, de modo que
. (10, 10)
La existencia de este campo eléctrico se ha demostrado experimentalmente por Kuehne.
Fig. 4
Nótese que relacionando los campos y definidos por (10, 8)y (10, 10), resulta que siempre que se produzca una traslación de líneas de fuerza irán juntas las de ambas clases, y esto de modo que , y tendrán las posiciones relativas que se señalan en la fig. 4, y además, trasladando el valor de H de (10, 8) a (10, 10) se obtiene
,
de donde que define la velocidad de los campos en un medio diferente del vacío. En este último caso, puesto que ε = μ = 1, c' = c. Conviene, además, recordar que la luz se reduce a un campo electromagnético tal como el que ahora estamos considerando, de modo que c' y c no son otra cosa que sus velocidades en el seno de un medio material y en el vacío, y teniendo en cuenta la definición del índice de refracción, .
También necesitamos recordar que cuando en (10, 9) se reemplaza H por su valor (10, 5) en función del vectos potencial se obtiene para el campo eléctrico inducido
.
Y si a él se agrega el originado por las cargas eléctricas, el campo total será
Es bien interesante notar que si se escribe y , las ecuaciones que acabo de escribir toman la forma
,(10, 11)
que recuerdan claramente las (10, 5).
Designando los campos y por una sola letra, h por ejemplo, con dos subíndices iguales y escritos en el mismo orden que los que afectan a las x en los denominadores de (10, 5) y (10, 11), se ve inmediatamente que estas ecuaciones imponen a las h las condiciones
,(10, 12)
donde i, j, k representa una cualquiera de las cuatro coordinaciones que pueden formarse con los números 1, 2, 3, 4 tomados tres a tres. Así, habrá cuatro ecuaciones del tipo (10, 12) entre las seis componentes de ambos campos, que en definitiva expresan que dichos campos derivan de los potenciales Pi mediante las ecuaciones (10, 5) y (10, 11). Por consiguiente, son postulados fundamentales para la teoría de los fenómenos electromagnéticos.
Es indispensable advertir que (10, 3) y (10, 7) son aplicables únicamente al caso en que la distribución de las cargas eléctricas, así como los valores de sus velocidades en los diferentes puntos del espacio, no cambian con el tiempo. Esto es lo que se llama una distribución estacionaria o permanente. Si se hace desaparecer tal restricción, como conviene a una teoría general de los fenómenos, aparecen en ambas ecuaciones términos que contienen las derivadas segundas de Φ y P convirtiéndolas en
Estas ecuaciones son también cuatro en número, como las (10, 12), y si en ellas se escribe como antes , pueden agruparse en la
,(10, 14)
donde Ci, representa a para los valores de 1, 2, 3 de i, mientras . Este grupo de ecuaciones es también fundamental para la teoría, y establece la relación entre las cargas eléctricas y los campos que engendran.
Es un hecho experimental que las cargas obedecen a la ley general de conservación, de suerte que la pérdida de electricidad sufrida por un volumen del campo es igual a la cantidad que durante el mismo tiempo atraviesa su superficie. Dicho de otro modo, las cargas eléctricas se mueven como un líquido incomprimible, fenómeno que, según la hidrodinámica enseña, se representa por la ecuación
,
de donde, en virtud de (10, 13)
,(10, 15)
cuya ecuación reduce la indeterminación del vector potencial a una constante.
Es interesante notar que a más de las ecuaciones fundamentales (10, 12), que ya dije expresan la existencia de los potenciales Pi para el campo electromagnético, y de la ley de conservación de la carga eléctrica, traducida por (10, 15), puede admitirse un principio equivalente al de Hamilton (§ 5) para el campo electromagnético, y entonces las cuatro ecuaciones (10, 14) se pueden deducir como corolarios de la teoría. He aquí una primera justificación de la generalidad que dije tiene el principio en cuestión.
d) Ambos campos, eléctrico y magnético, actúan sobre la materia y son capaces de ponerla en movimiento. Cuando se trata de esta acción es consecuencia de las cargas aparentes en los cuerpos y su valor se obtiene mediante el producto de por dichas cargas. La acción de se ejerce siempre que existan cargas en movimiento, y su valor para las positivas es , con la dirección que representa la fig 5. En definitiva, la acción total sobre la carga e será para el caso en que μ = 1
, (10, 16)entendiéndose, dicho se está, que se trata de una composición de vectores y no de una suma aritmética, y que la dirección del último sumando es normal a y , según dije ya.
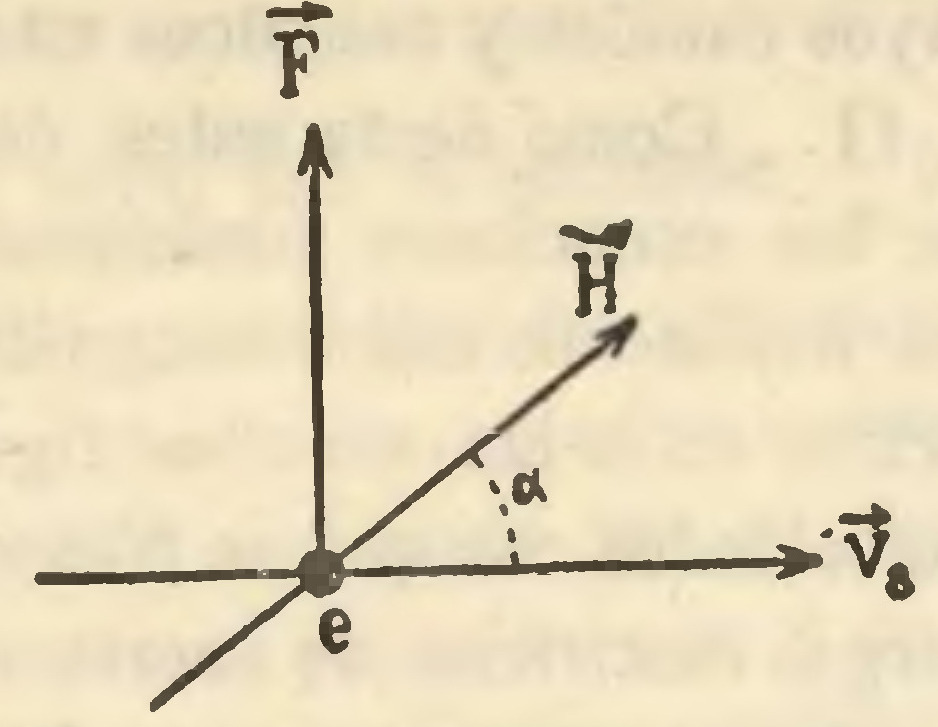
Fig. 5.
Las cargas en movimiento pueden mostrarse directamente, como en los casos de un cuerpo electrizado, de los iones gaseosos y de los rayos α y β de las substancias radioactivas, pero pueden escapar a la observación, como las que forman la corriente que circula por un conductor o en las moléculas de los cuerpos magnéticos (corrientes de Ampère).
La confirmación de (10, 16) resulta de todos los experimentos de la Electrostática y el Electromagnetismo, y muy particularmente de los realizados al estudiar las desviaciones que y producen sobre los iones positivos y negativos que constituyen los rayos canales y catódicos en los tubos de vacío.
11.
Como decía antes de comenzar el bosquejo de las ecuaciones fundamentales para la teoría de los fenómenos electromagnéticos, y como caso particular de la luz, en ellas figuran explícitamente las velocidades con que se transportan los campos y las cargas eléctricas, de suerte que un cambio de sistema de referencia ha de modificar los fenómenos aparentes. De otro modo, cuando una vez estudiadas las leyes que los rigen para un observador que se halle en reposo relativamente al sistema en que aquéllos se producen, efectuamos en sus expresiones analíticas las transformaciones indicadas por el grupo de Galileo, con el fin de conocer las leyes que serán válidas respecto de otro observador dotado de un movimiento rectilíneo y uniforme relativo a aquél, hallamos diferencias que contienen explícitamente la velocidad y permiten determinarla. Fué Hertz quien primero hizo esta aplicación de las ecuaciones de transformación de Galileo, con lógica innegable en atención a las ideas dominantes en su época.
Las consecuencias que así se derivan están, sin embargo, en absoluta contradicción con los resultados experimentales. Citaré dos ejemplos que ofrecen el mayor interés y son típicos:
a) En primer término, supongamos una onda luminosa que avanza en el seno de un cuerpo transparente. Para un observador en reposo, según he dicho antes, su velocidad se mide por el cociente (de la velocidad en el vacío por el índice de refracción). Para un observador que se mueva relativamente al cuerpo con velocidad ± V, indicando por el signo el sentido del movimiento en relación con el de la propagación, las ecuaciones de Galileo obligan a pensar que la velocidad de la onda debe ser .
Mucho antes de que Hertz formulara la teoría general, uno de cuyos corolarios es la predicción teórica anterior, Fresnel dió la interpretación de ciertos experimentos de Arago, que corresponden al mismo orden de ideas, pero son de naturaleza bastante más compleja, suponiendo que en la fórmula anterior y ha de multiplicarse por el factor
, que se denomina de arrastre, por razones de que me ocuparé más adelante. La existencia real de dicho factor fué confirmada experimentalmente por Fizeau, en trabajos que serán siempre considerados como modelos de ingenio y precisión, en los cuales el cuerpo en movimiento fué el agua. Posteriormente, con la mayor perfección que consiente la técnica moderna, ha sido también comprobado por Michelson y Morley y por Zeeman, siempre en el mismo líquido. El trabajo de este último deja además fuera de duda la presencia del sumando adicional
(donde τ es el período) que corresponde a la dispersión. Los resultados numéricos de Zeeman están contenidos en la tabla siguiente:
| λ en A° | φF | φL | φ exp. |
| 4500 | 0,443 | 0,464 | 0,465 |
| 4580 | 0,442 | 0,463 | 0,463 |
| 5461 | 0,439 | 0,454 | 0,451 |
| 6870 | 0,435 | 0,447 | 0,445 |
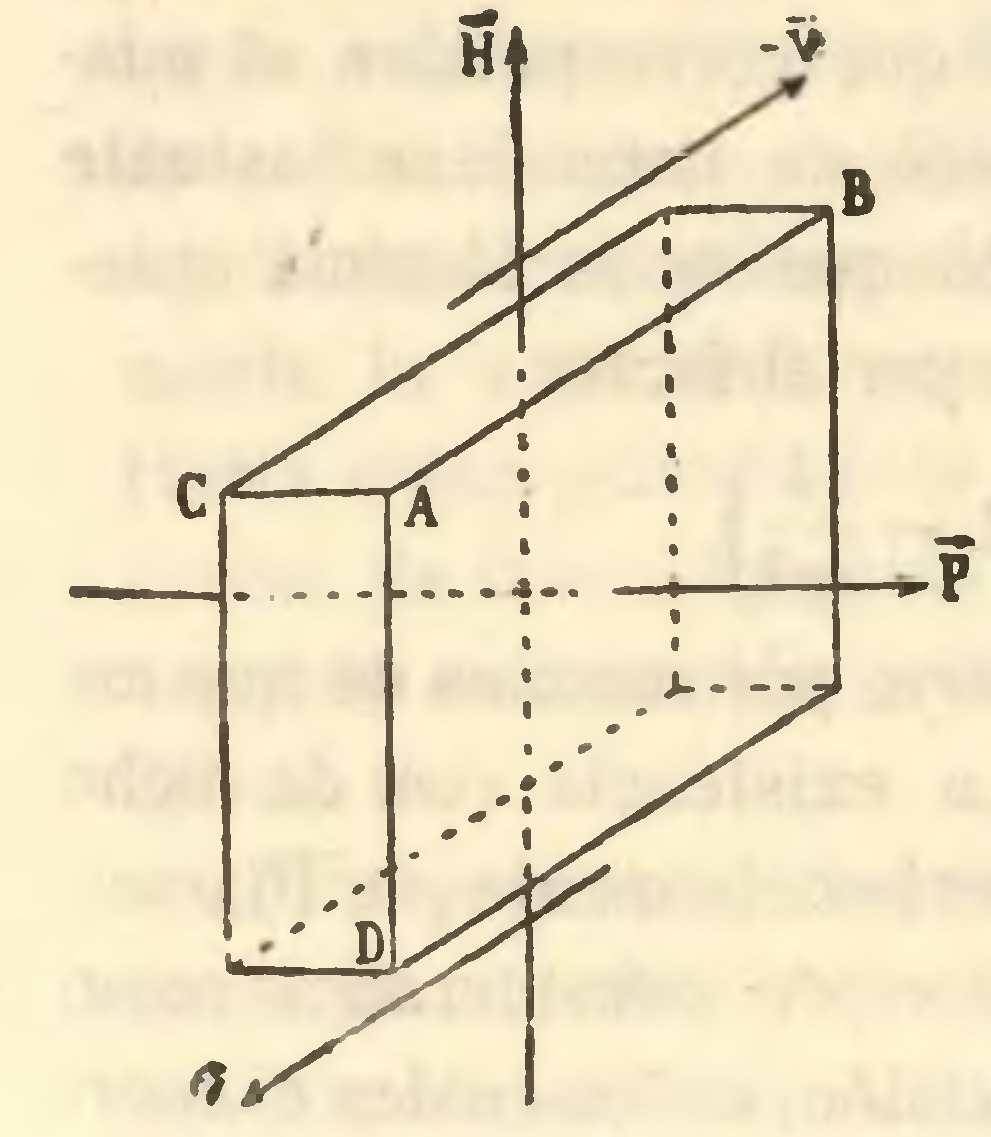
Fig. 6.
Aun con posterioridad, Zeeman y Snethlage han demostrado que la teoría se verifica con exactitud comparable en el cuarzo.
b) En segundo término, imaginemos un prisma dieléctrico ABCD (fig. 6) de constante ε, cuyas dos caras paralelas al plano ABD son conductores, fijo en el espacio, donde existe un campo magnético que la mayor perfección que consiente la técnica moderna, ha sido también comprobado por Michelson y Morley y por Zeeman, siempre en el mismo líquido. El trabajo de este último deja además fuera de duda la presencia del sumando adicional
(donde τ es el período) que corresponde a la dispersión. Los resultados numéricos de Zeeman están contenidos en la tabla siguiente:
| λ en A° | φF | φL | φ exp. |
| 4500 | 0,443 | 0,464 | 0,465 |
| 4580 | 0,442 | 0,463 | 0,463 |
| 5461 | 0,439 | 0,454 | 0,451 |
| 6870 | 0,435 | 0,447 | 0,445 |

Fig. 6.
Aun con posterioridad, Zeeman y Snethlage han demostrado que la teoría se verifica con exactitud comparable en el cuarzo.
b) En segundo término, imaginemos un prisma dieléctrico ABCD (fig. 6) de constante ε, cuyas dos caras paralelas al plano ABD son conductores, fijo en el espacio, donde existe un campo magnético que son los únicos, ponen bien en evidencia cómo la aplicación del grupo de Galileo a los fenómenos electromagnéticos resulta completamente injustificada, por lo menos en la forma en que fué hecha por Hertz.
Pero antes de seguir adelante, conviene advertir que ni el sabio alemán ni los demás físicos, en la época en que esta cuestión surgió, la plantearon en los términos en que lo he hecho. Por entonces la existencia del éter se consideraba innegable, y así Lord Kelvin podía decir que teníamos un conocimiento de su naturaleza más completo que de la materia ordinaria, puesto que todo lo que habíamos de exigirle estaba contenido en aquellas ecuaciones del campo electromagnético que he recordado arriba.
Precisamente la seguridad que esta opinión revela nace del papel principalísimo que la Mecánica de Newton desempeñaba en la Física. Esenciales en ella son los teoremas de conservación de la cantidad de movimiento y de la energía para los sistemas aislados, así como la distinción radical entre materia y energía, que otorga a aquélla la condición de soporte de las magnitudes y ℰ. Ahora bien: los teoremas indicados dejan de cumplirse para los fenómenos electromagnéticos cuando no se admite la existencia del éter.
Comenzaré por la conservación de . Imaginemos un foco radiante electromagnético E (fig. 7), luminoso o de ondas hertzianas, fijo al foco geométrico de un espejo parabólico, para que los rayos salgan del sistema en una dirección única. A larga distancia de este aparato emisor, supondré otro, A, que recoja y absorba íntegramente la energía de aquellos rayos. La teoría demuestra que sobre cada sistema, respectivamente durante la emisión y la absorción, actúan fuerzas, FE y FA, iguales y dirigidas según la recta que los une; pero cuyos sentidos son opuestos, pues el de la primera es contrario, y el de la segunda, idéntico al de propagación del haz.

Fig. 7.
La experimentación ha comprobado exactamente la realidad de FA, gracias, principalmente, a los trabajos de Nicholson y Hull, y si no se ha logrado también para FE, hay que atribuirlo a las insuperables dificultades técnicas que se oponen a la realización de los experimentos indispensables.
Las cosas ocurren del mismo modo que cuando se dispara un arma de fuego sobre un péndulo balístico: el choque de retroceso en el arma es igual al impulso que el péndulo recibe por la acción de la bala, despreciado el efecto del aire. En uno y otro caso, las acciones inicial y final son iguales y opuestas, como exige el tercer postulado de Newton; pero no actúan sobre el mismo sistema rígido ni son simultáneas, requisitos también indispensables.
Para este último caso no existe problema, porque el retroceso del arma equivale a la cantidad de movimiento que la bala recibe, y la destrucción de tal cantidad al encontrar la bala al péndulo constituye el origen del impulso. Esto parece indicar que el acuerdo de los fenómenos radiantes con la Mecánica ha de lograrse admitiendo que la radiación electromagnética transporta también una cantidad de movimiento, gracias a la cual el impulso que corresponde al retroceso del aparato emisor E se transmite al absorbente A.
Notemos aún que también existe incumplimiento aparente del principio de la conservación de la energia en el caso referido. En efecto; el foco emisor E consume energía que sólo vuelve a ponerse en evidencia cuando, andando el tiempo, la energía es absorbida en A. Entre el momento en que el consumo se produce y aquel en que la energía se hace sensible nuevamente, nada sabemos de ella, y este intervalo puede ser muy largo: centenares de años a veces. Baste recordar que la energía que supone la reducción de la sal de plata en una placa fotográfica en que se recoja la imagen de ciertos conjuntos estelares corresponde a una emisión luminosa que se produjo hace millares de años a distancias de nuestro sistema solar que la imaginación no acierta a representarse. Así, para retener el principio de la conservación de la energía, ha de pensarse que la luz la transporta en su carrera, como la bala de que antes hablaba acarrea en forma cinética la energía del explosivo desde el alma del cañón hasta el lugar donde han de producirse sus efectos destructores.
Si pudiéramos dejarnos arrastrar por la analogía con el ejemplo de que vengo sirviéndome, caería en la hipótesis de la emisión de partículas luminosas, que Newton defendió con tanto ahinco contra los argumentos de Huyghens, y que los clásicos experimentos interferenciales de Young y Fresnel arruinaron de manera definitiva, sustituyéndola por la teoría de las ondulaciones. Pero ello no supone ninguna dificultad, porque es bien sabido que las ondas que se producen en los medios materiales transportan también cantidad de movimiento y energía, aunque en ellas no haya acarreo de materia. Basta, pues, que el universo entero, en toda la extensión que la luz puede recorrer en tiempos infinitos, esté lleno de algo material capaz de transmitir las ondas luminosas con la enorme velocidad de 300.000 kilómetros por segundo: este medio universal es el que los físicos han llamado éter, y que, según decía arriba, creyeron conocer con mucha mayor precisión que la materia misma, puesto que sólo le exigían servir de soporte a los campos eléctrico y magnético.
En él se encuentran sumergidos todos los cuerpos, no como un sólido en el seno de un flúido, desalojándole del espacio que ocupa, sino que en él se bañan por igual hasta las últimas partículas que los integran, estableciéndose la ligadura entre ambas substancias, materia y éter, gracias a las cargas eléctricas que son elemento integrante, quizás único, de aquélla.
13.
Pero si el éter es el soporte de los campos y , cuando hablamos de velocidades de estos campos en las leyes fundamentales, ha de entenderse respecto de un sistema de referencia ligado a él, y los fenómenos que se produzcan por efecto del movimiento de los cuerpos dependen esencialmente de la respuesta que se dé a la siguiente pregunta: la materia en su movimiento ¿transporta al éter que la empapa? La hipótesis de Hertz, que discutí más arriba, equivale a que aquélla sea afirmativa, que hemos de convenir se ofrece al espíritu como la concepción más sencilla.
Mas los experimentos recordados antes por vía de ejemplo, prueban que es indispensable renunciar a tal hipótesis y suponer, bien un arrastre parcial del éter, según admitió Fresnel y de donde procede el nombre del coeficiente φ, bien su reposo absoluto en tanto los cuerpos se mueven en su seno, solución ésta, indudablemente, más lógica. Claro que entonces es indispensable explicar el arrastre parcial que los referidos experimentos denuncian, y el mérito de ello corresponde a H. Lorentz.
Según el profesor holandés, siguiendo ideas clásicas de Mossoti, el campo determina en cada átomo de los cuerpos materiales una separación de las cargas positivas y negativas, análoga a la que produce en los conductores y que se manifiesta en la influencia eléctrica. El fenómeno de conjunto que podemos apreciar es una polarización de componentes pi, que se traduce por la aparición de cargas eléctricas positivas en la superficie del dieléctrico por donde el campo sale, y negativas en aquellas por donde entra; numéricamente la densidad de estas cargas es ± (ε − 1) E. Así, en el experimento de Wilson, al mover el dieléctrico son estas cargas
,
reemplazando E por su valor (10, 9), de acuerdo con el resultado obtenido.
Análogamente, el cambio de velocidad que la luz sufre al penetrar en un cuerpo transparente se debe a la alteración periódica de la polarización de sus átomos, originada por el campo eléctrico de la onda luminosa. Dicha polarización periódica convierte cada átomo en un foco luminoso secundario cuya emisión se superpone a la luz incidente, dando lugar a una onda compleja, que es aquella a quien se refiere la medida de la velocidad dentro del cuerpo. Claro es que el movimiento de la materia afecta únicamente a esta luz secundaria, sin que en nada modifique a la onda que penetró en ella, y sigue avanzando a través del éter fijo, y un cálculo detallado demuestra que esto se traduce por un aparente arrastre parcial de la onda compleja, que coincide con el calculado por Fresnel.
Además existe otro fenómeno, de largo tiempo conocido, que prueba aún de modo más concluyente el reposo del éter mientras la materia se transporte en su seno. Me refiero a la aberración de la luz.
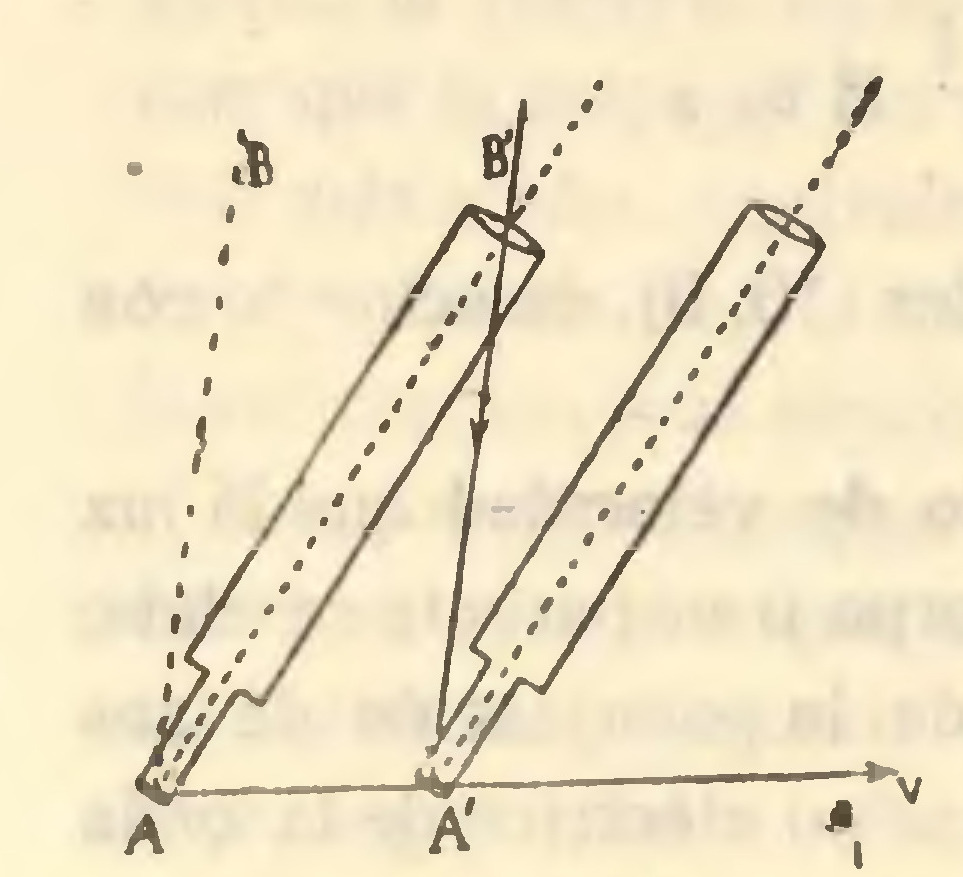
Fig. 8.
Cuando se ha de mirar un astro con un anteojo, no se apunta en la dirección AB (fig. 8) en que éste se encuentra en el momento de la observación, sino que el eje óptico AC ha de formar con AB un ángulo dependiente de la velocidad de la Tierra: el necesario para que la onda luminosa que pasa por el centro óptico del objetivo llegue a la cruz filar en el instante en que ésta se encuentra sobre el rayo. Esto Fig. 8 significa que nuestro movimiento no perturba a la onda en su propagación, puesto que el anteojo se orienta precisamente según requeriría la regla de composición de las velocidades y , supuestas perfectamente independientes, y tratándose de un movimiento ondulatorio, equivale a suponer que avanzamos en el éter sin arrastrarlo. Realmente esta consecuencia del fenómeno de la aberración no pareció tan evidente a muchos de los físicos que han discutido este asunto, uno de los que más preocuparon la opinión científica en los días en que se afirmó la teoría ondulatoria de la luz.
Fueron varios los experimentos efectuados con el fin de denunciar el movimiento de la Tierra a través del éter, siempre con resultado negativo, y de los cuales no me ocupo porque muy pronto he de llamar la atención sobre otros más perfectos realizados posteriormente; y en presencia de este fracaso permanente, lo más lógico era suponer que el éter es arrastrado. Para que ello no dejara a la aberración huérfana de explicación, Stokes sugirió que el éter tiene una constitución tal que se comporta como un flúido sin viscosidad para los movimientos lentos, y como un sólido de elevada rigidez para las vibraciones muy rápidas. Ello permitiría a las ondas luminosas propagarse con la velocidad que ellas lo hacen, y al propio tiempo haría que estas ondas, al pasar de una región del éter en reposo a otra arrastrada por la Tierra, no cambiasen la orientación de su frente. Pero las dificultades que entonces surgen son grandes, y de ellas se deduce con plena evidencia que las ideas de Stokes son un mero expediente para soslayar una dificultad, no una construcción teórica perfectamente lógica, por lo cual no vale la pena de detenernos más en su análisis [1].
Diré aún que la explicación del fenómeno que nos ocupa por una composición de la velocidad de la Tierra con la de la luz sugiere la posibilidad de que su magnitud sea función de la naturaleza del medio en que aquélla se propaga, como pensó Boscovich; pero atendiendo a la interpretación dada para el coeficiente de arrastre de Fresnel, se comprende, sin más detalle, que tal influencia no exista, de acuerdo con el efecto negativo a que llegó Airy estudiando la aberración con un anteojo lleno de agua.
14.
Notoriamente, la existencia de un éter en permanente reposo, mientras los cuerpos se trasladan en su seno, equivale a negar la equivalencia de todos los sistemas de coordenadas, que sólo difieran en un movimiento rectilíneo y uniforme, y, por tanto, la universal aplicación del principio de relatividad, válido en la Mecánica. Los ejes de referencia que se hallen fijos al éter ocupan una posición privilegiada, según demuestran los resultados de la observación y la experiencia recordados anteriormente: la misma simplicidad de naturaleza que se atribuyó al medio universal, en cuanto sólo se exigía de él que sirviera de soporte a los campos eléctrico y magnético, permite que se le sustituya por el sistema de ejes privilegiados a que aludía, caracterizados porque con relación al mismo las ecuaciones fundamentales de los fenómenos electromagnéticos tienen forma definida. Y entonces claro es que puede hablarse de velocidades absolutas en el espacio, dando a este término el sentido de velocidad relativa a dicho sistema privilegiado.
Supongamos, por ejemplo, que en un instante determinado t0 y en el lugar del espacio 0 (fig. 9) en que entonces nos hallemos, producimos un destello luminoso. La onda avanzará en el éter con velocidad constante c en todas las direcciones, formando una esfera de radio creciente, pero cuyo centro permanece clavado en el mismo lugar 0 donde se produjo el destello. Entre tanto, nosotros avanzamos con velocidad , de suerte que la distancia que nos separará de la cresta de la onda en cualquier tiempo t1 posterior, cambiará con la dirección, y como el cociente de dicha distancia por t1 - t0 mide la velocidad aparente de la luz, esta magnitud variará entre c - V, para la dirección de nuestro movimiento, y c + V para la opuesta.
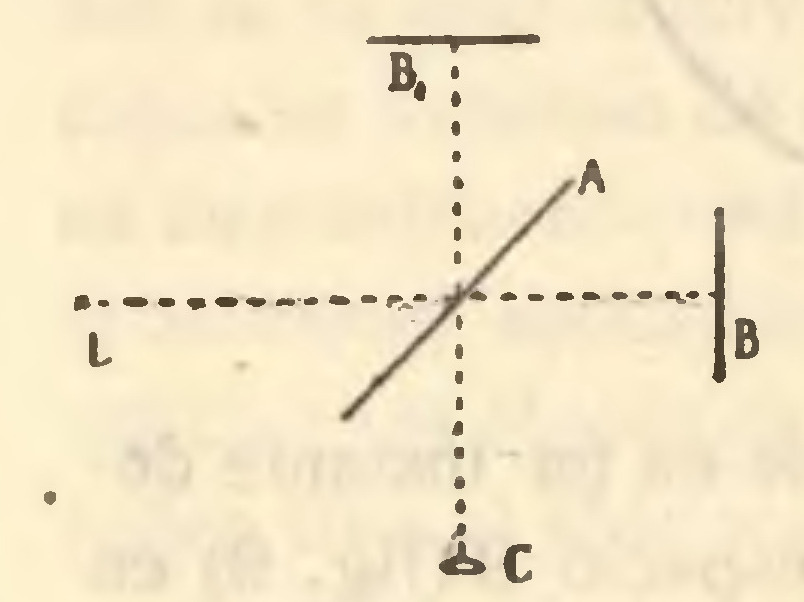
Fig. 10.
Naturalmente, la realización de este experimento debe dar un método para medir sin acudir a ningún fenómeno extraterrestre. Michelson ideó en 1887 un método de sensibilidad suficiente para efectuar estas medidas y apreciar el valor de , aunque esta magnitud no llegue al valor de la velocidad de la Tierra en su órbita, de modo que . Para este fin, y reduciendo la descripción a lo estrictamente esencial, un haz de luz procedente del foco L (fig. 10) encuentra un lámina semitransparente A, donde se bifurca en el rayo AB, continuación del haz primitivo, y el AB1, perpendicular a él. A distancia igual, (l), para ambos rayos se encuentran los espejos B y B1 que los reflejan nuevamente hacia A1, y allí cada uno se bifurca del mismo modo que el haz primitivo. Basta considerar los semirrayos que se propagan según AC y vienen a sumar sus efectos en C.
Si el sistema se hallase en reposo relativamente al éter, como los caminos que los dos rayos han hecho son iguales y las velocidades con que los han recorrido idénticas, al superponerse según AC sus fases serán perfectamente concordantes y en dicha dirección la intensidad será máxima. Pero cuando el sistema se mueve, las diferencias en la dirección de los rayos ABA y AB1A engendran un retardo en el uno respecto del otro, que ha de compensarse considerando rayos que formen un ángulo ligero respecto del primitivo, pues entonces los caminos no serán iguales. Así, se producirá un corrimiento de la franja de máxima intensidad respecto de su posición en el caso anterior, que es el fenómeno observable.
El cálculo del retardo indicado es fácil, cuando se supone la velocidad coincidente con uno de los rayos, según se hace ya en la figura. Entonces, de A a B la luz avanza en el sentido de , con lo cual su velocidad aparente será c - V, y de B a A la dirección es opuesta, y esta última magnitud tendrá el valor c + V. En definitiva, el tiempo invertido por la onda desde que pasa por A hasta que vuelve a dicho punto será:
En cuanto al rayo AB, ha de tenerse en cuenta 
Fig. 11.que mientras la luz va de uno a otro punto, el aparato se corre en el sentido de , de modo que la velocidad aparente será el cateto perpendicular a V del triángulo de la figura 11; esto es , y cosa idéntica ocurre en el recorrido de vuelta de la onda. Asi el tiempo total será:
El retardo se medirá evidentemente por
Haciendo girar a todo el aparato 90°, las direcciones AB y AB1 se cambian, con lo cual el retardo se invierte. Así, el corrimiento observado, pasando de una posición a otra del sistema, será doble de (14, 1), y expresado en fracción de la distancia que separa a las bandas de interferencia observadas en C, será:
Posteriormente a la realización por Michelson y Morley de este experimento ha sido repetido por Morley y Miller, mejorando la disposición en forma que permitía apreciar una centésima del efecto previsto, no obstante lo cual, los resultados fueron negativos, y esto sea cual fuera la época del año en que se obtuvieron.
Es definitiva, la velocidad de la luz, no obstante el movimiento de la Tierra, es independiente de la dirección en que se determine, resultado cuya interpretación más directa es el arrastre del éter por los cuerpos que en él se mueven, en oposición a los experimentos citados precedentemente.
15.
No se trata de un experimento aislado. Tal circunstancia quitaría un poco de valor a las consecuencias de él derivadas, no obstante la gran precisión del mismo y la variedad de condiciones en que fué ejecutado, gracias a todo lo cual, ha podido resistir a una crítica bien persistente que apenas si ha cesado. Aun muy recientemente Righi creyó encontrar una causa de error en la interpretación del experimento, que ha sido rebatida por varios físicos y, entre ellos, por el español P. de Rafael.
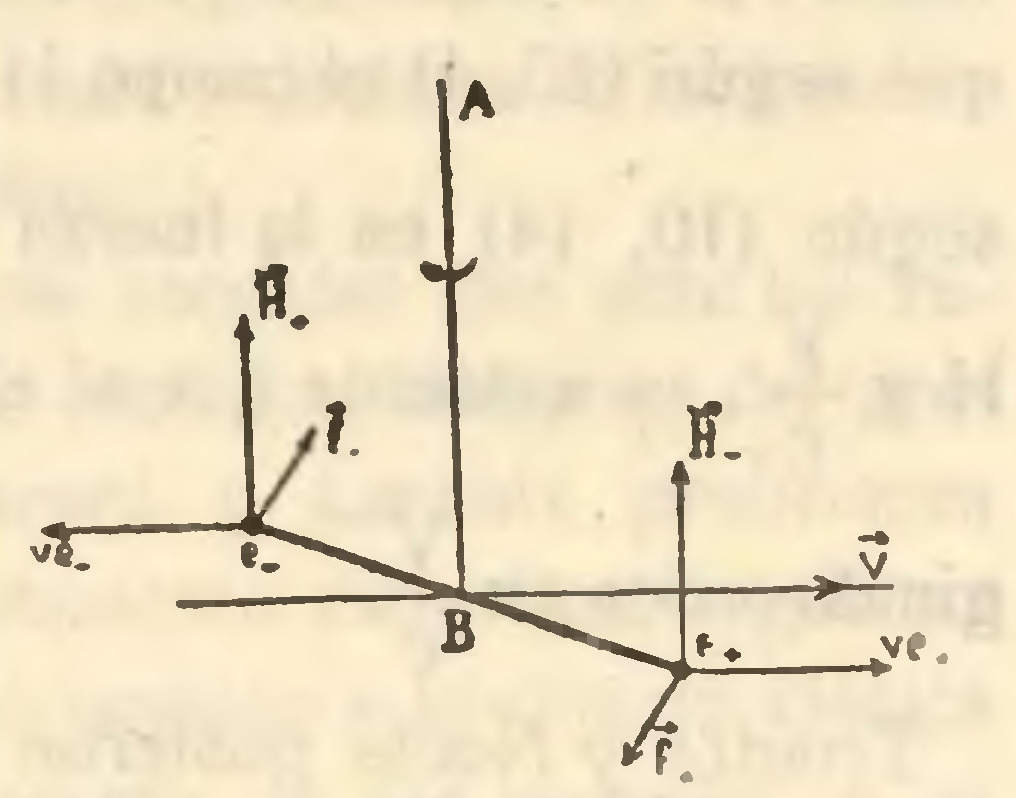
Por otros caminos se llegó a la misma conclusión. Imaginemos dos cargas eléctricas numéricamente iguales, pero de signos opuestos, e+ y e-, sujetas en las extremidades de una varilla rígida (fig. 12) que va suspendida por un hilo AB de un soporte fijo a nuestro laboratorio. La tierra arrastra a este sistema con una velocidad que supondré no es perpendicular a la varilla. En la hipótesis del éter en reposo, como las ecuaciones de los campos han de referirse a los ejes en él fijos, cada carga produce un campo magnético cuyos valores H+ o H-, en el lugar ocupado por la otra, se han representado en la figura, claro que prescindiendo de toda escala. Entonces e+ y e- se hallan en movimiento en los campos magnéticos en cuestión y, por ende, experimentarán acciones que también están dibujadas, y, según se reconoce, engendran un par que tiende a torcer el hilo en la forma que la flecha curva señale. Puesto que según (10, 4) el campo H es proporcional a , y según (10, 14) en la fuerza figuran como factores H y , es evidente que el efecto previsto es de segundo orden en .
Trouton y Noble pusieron en práctica este método para denunciar nuestra velocidad en el éter, constituyendo el sistema rígido que lleva las cargas e+ y e- mediante un condensador. La rotación producida por el momento de la carga no pasó del 5 por 100 de la cantidad calculada, de suerte que es perfectamente atribuible a las perturbaciones inevitables.
También de aquí, como del experimento de Michelson, es necesario concluir que el éter es arrastrado completamente por la Tierra en su movimiento, en contradicción manifiesta con la aberración de la luz y los experimentos de Fizeau y Wilson. La consecuencia inmediata parece ser la admisión de una multiplicidad de medios cuyas propiedades son idénticas al éter y que existen superpuestos en cada punto del espacio, con cuya idea chocamos notoriamente, y es lógico que, al menos en un cierto momento de la historia de este capítulo de la ciencia, hayan sido muchos los físicos que, con Einstein y Planck, prefirieron prescindir de este medio, cuya existencia es corolario obligado de ciertos postulados de la Física. Naturalmente, ello equivale a declarar la bancarrota de los referidos principios.
Sin embargo, conviene recordar que ante los resultados contradictorios aludidos, hombres del profundo valer de Fitzgerard y Lorentz prefirieron aplicar el método estrictamente científico, según ya recordaba en el § 1, adicionando a la ciencia clásica la hipótesis del acortamiento de los cuerpos en el sentido del movimiento. Pero entonces era lógico presumir que este cambio de dimensiones se denunciase por una disimetría de constitución. Así, Lord Raylegh y Brace investigaron la existencia de una doble refracción en los cuerpos isótropos, y Trouton y Rankine, una diferencia en la conductividad metálica, sin que el éxito coronase las tentativas. Cierto que pueden buscarse mecanismos que permitan en cada caso la explicación de los resultados experimentales, como lo hiciera Lorentz para la doble refracción prevista por Lord Raylegh, pero es indudable que la misma complejidad que así se va creando en la Ciencia es una prueba de la arbitrariedad del método. Es preferible acudir al análisis de los postulados mismos que son los cimientos del edificio científico; lo cual equivale a la aceptación de la ruina completa de ésta, utilizando los hechos innegables aportados por la experiencia en la nueva construcción. En último término, esto representa la obra de Einstein.
- ↑ Puede verse una crítica más completa en Larmor, Æther and Matter.