Página:La teoría de la relatividad de Einstein.djvu/47

Esta página ha sido corregida

39

Leyes fundamentales de la mecánica clásica.

mejantes los triángulos M A B y C D E, y se obtiene la proporción:

{\frac {DE}{CD}}={\frac {AB}{MA}}

.

Ahora bien; $DE=w,CD=v$ , y, además, M A es igual al radio r y A B es igual al arco s con un pequeño error, que, eligiendo un pequeñísimo intervalo de tiempo t, puede reducirse cuanto se quiera.

Obtiénese, pues:

{\frac {w}{v}}={\frac {s}{r}}

; o sea

w={\frac {sv}{r}}

Dividamos por t' y observemos que

{\frac {s}{t}}=v

y que

{\frac {w}{t}}=b

;

de donde resulta:

b={\frac {v^{2}}{r}}

[3]

es decir: la aceleración centrípeta es igual al cuadrado de la velocidad de revolución dividido por el radio del círculo.

Sobre esta proporción descansa, como veremos, una de las primeras y más importantes demostraciones experimentales de la teoría newtoniana de la gravedad.

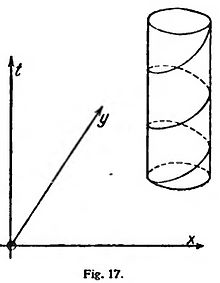
Acaso no sea superfino manifestar claramente cuál es el aspecto que el movimiento circular uniforme presenta en la exposición gráfica, como curva en el espacio xyt. Esta curva se produce manifiestamente haciendo que el punto móvil suba paralelamente al eje t y uniformemente, mientras se verifica el movimiento circular; obtiénese, pues, una línea helicoidal, o sea en forma de tornillo, que representa integramente la tra-