cm., por sec. o cm./sec. Para expresar que las medidas de velocidad se reducen, según la fórmula [1], a medidas de longitud y de tiempo, dícese que la velocidad divide la dimensión longitud por el tiempo; esto es, . De modo correspondiente coordínase una determinada dimensión a toda magnitud que se construya con las magnitudes fundamentales: longitud l, tiempo t y peso G. Sabido esto, puede expresarse en seguida la unidad de la magnitud por las de longitud, de tiempo y de peso, cm., sec. y g.
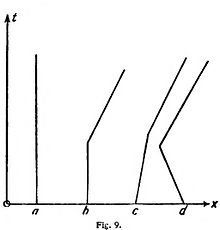
En las grandes velocidades, el camino x, recorrido en el tiempo t es grande; la recta que lo expresa en la figura correrá casi paralela al eje de las x; cuanto más pequeña sea la velocidad, tanto más se acercará la recta a la posición perpendicular al eje de las x. Un punto inmóvil tiene una velocidad igual a cero, y en nuestro diagrama será representado por una recta paralela al eje de las t, pues los puntos de esta recta tienen el mismo valor de x para todos los tiempos t (fig. 9, letra a).
Si un punto empieza estando inmóvil y luego de pronto, en un momento, recibe cierta velocidad y se mueve con esa velocidad, obtenemos la imagen de una quebrada, cuya parte primera es vertical (fig. 9, letra b). Si el punto se mueve primero hacia la derecha o hacia la izquierda con movimiento uniforme, y de pronto varia su velocidad, obtendremos igualmente líneas quebradas ({{#fig9|fig. 9]], letras c, d).
Si la velocidad anterior a la súbita variación es v1 (por ejemplo = 3 cm./sec.) y luego es v2 (por ejemplo = 5 cm./sec), en-
![{\displaystyle [v]=[{\frac {l}{t}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38d88095b67999bbf05cb9a9c7bb9d70ef974cd3)
