Compete al agrimensor introducir la medida en esa numeración de los puntos del terreno. Su cinta métrica alcanzará, por ejemplo, la extensión de una malla en la red de las coordenadas de Gauss.
El agrimensor empezará luego a medir malla por malla; cada una de éstas puede considerarse como un pequeño paralelogramo y queda determinada por dos longitudes y un ángulo. El agrimensor tiene que medirlos y apuntarlos en el mapa en cada malla. Una vez realizado este trabajo, domina la geometría del terreno completamente merced a su mapa.
En lugar de los tres datos por cada malla— dos lados y un ángulo—suele emplearse otro método que tiene la ventaja de una mayor simetría.
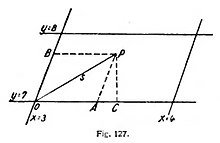
Consideremos una malla, un paralelogramo, cuyos lados corresponden a dos números enteros consecutivos—por ejemplo: x = 3, x = 4 é y = 7, y = 8 (fig. 127)—. Sea P un punto cualquiera en el interior; su distancia al vértice O, señalado con el número más pequeño, es s. Esta distancia se mide con la cinta métrica. Por P tracemos las paralelas a las líneas de la red, que encontrarán a éstas en A y B. Sea, además, C el pie de la perpendicular bajada de P a la línea coordenada x.
Los puntos A y B tienen también números o coordenadas de Gauss en la red; se determina A, por ejemplo, midiendo el lado del paralelogramo en que está A y la distancia AO, y entonces la relación de ambas longitudes se tomará como aumento de la coordenada x de A con respecto a O. Señalaremos este aumento mismo con la letra x, eligiendo O como punto cero de las coordenadas de Gauss. De igual manera determinamos la coordenada gaussiana y, de B, como la relación en que B divide al correspondiente lado del paralelogramo. En-
