Supongamos ahora que los tres puntos A, B y C se mueven uniformemente con igual velocidad; sus líneas universales serán nuevamente paralelas, pero oblicuas sobre el eje x (fig. 110). Las señales luminosas son representadas por las mismas líneas anteriores que parten de C; pero sus intersecciones A1' y B1' con las líneas universales A y B no están ahora situadas en una paralela al eje x; no son, pues, simultáneas en el sistema de coordenadas xt, sino que B1' es posterior a A1'. En cambio, un observador que se mueva con el sistema, afirmará con igual derecho que A1'B1' son sucesos (puntos universales) simultáneos; este observador usará un sistema S' de coordenadas x't', en el cual los puntos A1' y B1' estarán en una paralela al eje x. Las líneas universales de los puntos A, B y C son, naturalmente, paralelas al eje t' por A, B y C en el sistema S' están inmóviles, y sus coordenadas x' tienen el mismo valor para todos los t'.
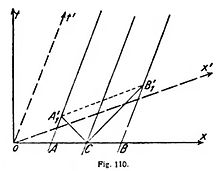
De aquí se deriva que el sistema en movimiento S' en el plano xt es representado por un sistema de coordenadas a ángulo agudo x't', en el cual los dos ejes están inclinados con respecto a los primitivos.
Recordaremos que en la mecánica corriente los sistemas inerciales eran representados en el plano xt también por coordenadas acutangulares con eje t dirigido de cualquiera manera, quedando empero el eje x siempre idéntico (III, 7, pág. 86). Ya allí hubimos de advertir que esto es, desde un punto de vista matemático, un defecto de belleza que la teoría de la relatividad suprime. Ahora se ve claramente cómo ello se realiza merced a la nueva definición de la simultaneidad. Al mismo tiempo, con sólo mirar la figura, sin necesidad de cálculos se
